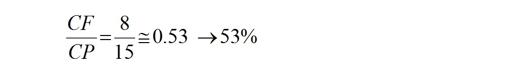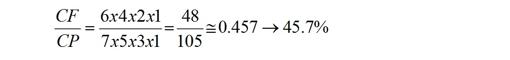El problema matemático de la cuerda anudada que dice si te puedes casar
El problema matemático de la cuerda anudada que dice si te puedes casar |
 |
 |
 |
|
ABC, 19 de Junio de 2017 Una pareja solo podrá celebrar su boda si consigue atar unos cabos de dos en dos hasta formar un anillo. Un agudo cálculo de probabilidades con un resultado sorprendente
Las apariencias ¿engañan? En los dominios de la probabilidad y el azar con cierta frecuencia. Una de las muletillas del lenguaje habitual es aquello de ‘evidentemente’ situado entre dos oraciones y si ya lo normal es que no haya ninguna evidencia en lo que se concluye, en algunos ámbitos no sabemos siquiera si estamos en condiciones de reivindicar la evidencia. Para ejemplificar esta entradilla vamos a trasladarnos con la imaginación a un territorio llamado «Machuria», cuyo nombre no es casualidad, porque no está situado en un lugar concreto, sino bastante extendido en el tiempo y en el espacio: el territorio del machismo. Y vamos a contar una historia que sucedía (y me gustaría pensar que ya es pasado) cuando una chica quería casarse: tenía que pedir permiso a la ‘autoridad’. Para hacerlo iba junto con el chico con el que se había prometido al palacio del ‘jefe’ y este ponía en la mano cerrada de la chica seis trozos de igual longitud de una cuerda fina que sobresalían por los dos lados de su mano; su pretendiente tenía que ir uniéndolos (haciendo nudos) de dos en dos por cada lado de la mano sin que la chica la abriera, para no poder saber los extremos de cada una; cuando estaban hechos los seis nudos la chica abría la mano: si la cuerda salía formando un anillo podían casarse; si no tenían que postergar la boda.
Quizás no son las condiciones más complicadas del enorme territorio de Machuria. Pero centrándonos en estas, ¿somos capaces de evaluar lo difícil que era casarse en Machuria?; ¿podemos dar la probabilidad de que eso suceda? En las fotos a la izquierda aparece la situación inicial, y las tres posibilidades que hay cuando abrimos la mano después de atar los nudos. En la primera, la del único anillo, la pareja se puede casar; en las otras dos (tres anillos pequeños o dos anillos, uno pequeño y otro mediano) no tienen permiso para casarse.
Si hemos de hablar en términos de evidencias (aparte de tener pocas) parece ‘evidente’ que el ‘jefe’ del territorio no era muy amigo de los matrimonios entre sus súbditos, porque la probabilidad de que salga un solo anillo parece muy pequeña. ¿Pero estamos seguros de que las apariencias no engañan? Una primera aproximación a la respuesta sería decir que como hay tres casos posibles y en dos la respuesta es negativa, la probabilidad será de 1/3, algo más del 33%. Pero quizás hay que tomarlo con cuidado, porque la probabilidad es el cociente entre los casos favorables (CF) y los casos posibles (CP), pero con la condición de que todos los casos posibles sean igualmente probables, algo que no estamos en condiciones de asegurar en esta situación. Peor todavía.
Antes de pasar a dar la solución, como todo es empeorable en la vida, en un territorio cercano a Machuria estaban todavía más agudizados los defectos de los que mandaban: en Remachuria tenían un caíd todavía más reaccionario, que quería endurecer las condiciones de casamiento respecto a Machuria: aplicaría el mismo procedimiento que allí pero, en vez de con seis, con ocho trozos de cuerda fina (es necesario un número par de cuerdas para poder hacer los nudos). ¿Crees que es más difícil casarse en Remachuria o el caíd además de reaccionario es torpe en probabilidad? En cualquier caso, ¿puedes hallar también la probabilidad en Remachuria?
Si se tienen nociones de cálculo de probabilidades, ambas se pueden calcular. Pero en cualquier caso lo que se puede hacer es repetir unas cuantas veces el experimento para hacerse una idea aproximada de cuál es el orden de la probabilidad que buscamos. En estos aspectos las matemáticas son parecidas a las ciencias experimentales: podemos obtener el resultado de un problema por medio de la experimentación. El cálculo de probabilidades Vamos a hallar la probabilidad en Machuria calculando los casos favorables (CF) y los posibles (CP), todos ellos igual de probables. Atamos como queramos las cuerdas que salen por uno de los lados de la mano, porque no supone ninguna limitación de lo que sucederá al atar por el otro lado, y es en ese otro lado donde nos fijamos. Las maneras posibles de atar son las siguientes: en el primer nudo, elegido uno de los extremos lo podremos atar con cualquiera de los otros cinco (5 por tanto); hecho ese primer nudo, elegimos el segundo extremo, para lo que ya solo hay tres para elegir; y atado el segundo nudo ya solo nos quedan dos extremos sueltos y la única posibilidad de elección es atarlos entre sí. Por tanto: CP = 5x3x1 = 15 ¿En cuántos de esos casos sale un único anillo? Esos serán los CF. Elegido uno de los extremos, el primer nudo podemos hacerlo con todas las cuerdas excepto con aquella que ya está unida por arriba con ella: cuatro posibilidades; para el segundo nudo tenemos que evitar la cuerda que ya está unida por arriba con ella, dos casos; en el tercero solo quedan dos extremos, luego una sola opción. Con todo eso: CF = 4x2x1= 8 Con lo que la probabilidad de que salga un solo anillo y casarse por tanto será:
Un resultado sorprendente: ¡el resultado es positivo en más de la mitad de los casos! De los tres casos posibles el más frecuente (¡más que la suma de los otros dos, que solo se consiguen en el 47% de los casos!) es conseguir un gran anillo.
Eso le da, amable lector, una posibilidad de triunfar en reuniones sociales, además con poco dinero. Para ello puede comprar un ovillo de bramante (un lujo a su alcance) y hacer unos cuantos paquetes de seis cuerdas; proponga el ‘problema’ anterior, distribuya a la gente por parejas, entrégueles a cada una uno de los paquetes y que hagan el experimento varias veces: enseguida verán que más o menos la mitad de las veces les sale un gran anillo, como usted se había encargado de pronosticar, ante la desconfianza del resto. Nos cambiamos de territorio: pasamos ahora a Remachuria. Después de lo anterior, ¿estamos seguros de que la probabilidad es menor? Caso de serlo, ¿es mucho menor? Vamos a contestar a las preguntas. Razonando de la misma forma que en Machuria, la probabilidad será también el cociente entre los casos favorables y los posibles:
Baja, pero no mucho, quizás menos de lo que esperábamos. Y además seguirá bajando, poco a poco, si vamos aumentando el número de cuerdas. El ABCDARIO DE LAS MATEMÁTICAS es una sección que surge de la colaboración con la Comisión de Divulgación de la Real Sociedad Matemática Española (RSME) |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |