Las matemáticas que puede esconder un dónut
Las matemáticas que puede esconder un dónut |
 |
 |
 |
|
ABC, 3 de Noviembre de 2017 La explicación al descubrimiento de dos teóricos de los números que incluye dulces glaseados, curvas elípticas y la teoría de las locuras mostruosas
En un donut real, se percibe dónde están los confites. Sin embargo, si estuviéramos a oscuras no lo sabríamos sin tocarlo. Eso es lo que pasa con las curvas elípticas, que no sabemos dónde están dispuestos esos dulces (los puntos racionales), pero probablemente gracias al grupo de O’Nan sea más fácil descubrirlos
El pasado mes de septiembre algunos medios de divulgación norteamericanos se hicieron eco de una “sorprendente” noticia comunicada por los especialistas en teoría de números Ken Ono y John Duncan, de la Universidad Emory, institución privada de Atlanta, en el estado de Georgia. En su afán por hacer entendible a la sociedad el contenido de resultados técnicos, los redactores suelen intentar relacionar las noticias científicas con aplicaciones a nuestra vida cotidiana o a objetos familiares, y tratar de comprimirlo en el reducido espacio de texto que consideran apropiado antes de que el lector se canse y deje de leerlo para pasar a otra cosa más interesante o que al menos entienda. En definitiva, sin mayores explicaciones, y como suele decirse, acaba siendo peor el remedio que la enfermedad, ya que se monta un batiburrillo tal, que ni siquiera un especialista es capaz de reconocer algo medianamente ininteligible. En el caso que nos ocupa, se mezclaban dónuts glaseados con chispitas de colores, con el grupo de O’Nan, los parias, las curvas elípticas, la teoría de las locuras monstruosas, etc., y encima lo útil que resulta todo ello. Imaginen.
Empecemos por el principio. Como saben, las matemáticas han ido evolucionando a lo largo de la historia, yendo de lo particular (casos concretos) a lo más general. Los famosos teoremas, proposiciones, corolarios, lemas, etc., que conforman las diferentes disciplinas matemáticas (que sólo tienen validez y adquieren esas denominaciones después de una correcta y rigurosa demostración formal) son resultados lo más general y abstractos posibles, aplicables a multitud de situaciones que verifiquen las hipótesis correspondientes. En nuestra vida real también se hace algo parecido continuamente: un médico examina a un paciente para detectar unos determinados síntomas (es decir, comprueba las hipótesis que tiene) antes de aplicarle tal o cual tratamiento (el teorema correspondiente); un fontanero observa la avería (las hipótesis) antes de aplicar el remedio con las herramientas más apropiadas (los teoremas). El álgebra abstracta surge a principios del siglo XX estudiando lo que llamamos estructuras algebraicas, que no son más que conjuntos de objetos a los que se les aplica una o varias operaciones, y que verifican determinadas propiedades (axiomas). Una de esas estructuras son los grupos. Se llama así a todo conjunto que con dicha operación (suma, producto, derivar y dividir, la que sea, pudiendo ser también una manipulación geométrica, en definitiva, cualquier transformación a los elementos del conjunto) verifica tres propiedades básicas: asociativa, existencia de elemento neutro o identidad, y existencia de elemento opuesto. Además, debe cumplir que, al operar dos objetos cualesquiera del conjunto, no nos salimos de él, es decir, que el resultado vuelve a ser un elemento del conjunto (ley de composición interna, en nuestra jerga específica). Si además da igual el orden en el que operemos dos elementos cualesquiera (primero uno y luego el otro, o al revés), el grupo es además conmutativo o abeliano (en honor al matemático noruego Niels Henrik Abel). Vale, eso es un grupo, ¿y para qué lo definimos? Pues porque resulta que existen muchísimos conjuntos, en los más dispares contextos, que junto a la operación que les dota de esa estructura, se comportan todos del mismo modo. Por ejemplo, la estructura de grupo subyace en la comprensión de las simetrías (y éstas aparecen en los más variopintos lugares, desde composiciones artísticas, a la estructura interna de los átomos de los elementos químicos, por poner dos situaciones evidentes; o de nuevo en la seguridad de nuestras tarjetas de crédito, o en los métodos de resolución de juegos como el cubo de Rubik). Y los especialistas en teoría de grupos han descubierto y desarrollado muchos teoremas que pueden aplicar a cualquiera de estas estructuras para entender su comportamiento, o para resolver las situaciones en las que aparezcan.
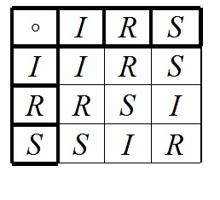
Vamos a ver un ejemplo concreto de grupo, muy sencillo, enmarcado precisamente en la simetría. Tomemos la conocida señal de tráfico de ceda el paso (un triángulo corriente con el vértice hacia abajo). Si giramos la señal 120º, 240º o 360º, a nuestros ojos la señal queda tal y como la vemos, como si no hubiéramos hecho nada sobre ella (tiene simetría rotacional), aunque la hemos aplicado tres operaciones diferentes, tres giros. Para verificar esos giros etiquetemos los vértices con letras, llamando a esas rotaciones I (giro de 360º; lo deja como está, es la identidad), R (giro de 120º), S (giro de 240º). ¿Qué sucede al combinar dos de esas operaciones? Por ejemplo, si hacemos un giro de 240º y luego uno de 120º (matemáticamente se denota por S ◦ R), evidentemente el resultado es el mismo que girar 360º, por lo que escribiríamos S ◦ R = I. De un modo similar podemos calcular todos los posibles pares de operaciones, y ordenarlos en una tabla, conocida como tabla de multiplicación, o tabla de Cayley (en honor al matemático Arthur Cayley).
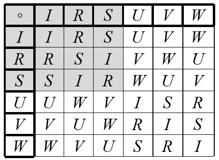
Pero la señal de tráfico tiene más simetrías. Las simetrías especulares, las que apreciamos si giramos la señal en torno a una recta (U, V, W son las tres posibles; por ejemplo, V sería dejar fijo el vértice inferior, y girar alrededor de la recta marcada, intercambiando los dos vértices superiores). Con esos seis elementos, la tabla de multiplicar que resume todas las posibles operaciones quedaría como muestra la siguiente imagen. El lector puede comprobar que vuelve a ser un grupo conmutativo, en este caso de orden 6. Y véase que contiene la tabla de multiplicar del grupo anterior, que se ha sombreado. Éste se denomina subgrupo, porque está contenido en el grupo de orden seis. A modo de curiosidad, obsérvese la similitud de este tipo de tablas con los sudokus: cada fila y columna tiene todos los elementos, sin repetir ninguno. Esto sugiere un par de cuestiones para que el lector se entretenga, si quiere: ¿Tiene cada sudoku la estructura de grupo, o sólo la tendrían unos pocos? De haberlos, ¿cuántos? Estos dos eran ejemplos de grupos finitos (el número de elementos que los generan es un número finito). Hay grupos que se generan a partir de otros, pero a los matemáticos nos interesan especialmente aquellos grupos que podríamos denominar “básicos” (algo parecido a los elementos químicos a partir de los que se generan los compuestos, o los números primos que generan cualquier número entero; los “ladrillos” con los que formar los demás, en definitiva), y hacer con ellos una clasificación. Matemáticamente se llaman grupos finitos simples. Un grupo simple es aquel que sólo contiene como subgrupos a la identidad y al grupo completo (éstos dos siempre son subgrupos de cualquier grupo), sin ningún otro entremedias; el de la señal de tráfico con los seis elementos no sería un grupo simple porque contiene un subgrupo propio (distinto de los dos mencionados) de orden tres. La definición rigurosa de grupo simple incluye otra condición (la de subgrupo normal) pero no entraremos en más detalles por no alargar ni complicar más la reseña. Pues bien, hacer esa clasificación de grupos finitos no ha resultado tan sencillo como podría suponerse a priori (en la próxima reseña les contaré curiosidades sobre esta clasificación que da origen al llamado teorema enorme que fue predicho en el cine antes de ser demostrado en la realidad). Casi todos estos grupos se adecuan en varias categorías, pero hay 26 grupos que no cuadran en ninguna de ellas. Se les llama por ello grupos esporádicos, y son de orden grande (el más pequeño es de orden 7920, conocido como M11; ese nombre se debe al matemático Emile Mathieu, que descubrió cinco de estos grupos entre 1860 y 1870). El más grande se conoce como el grupo monstruo de Fischer-Griess (o grupo monstruo, a secas), y se designa por M o por F1, y es de orden 808017424794512875886459904961710757005754368000000000 (un ocho seguido de 53 ceros aproximadamente; en efecto, es lo que piensan, es un grupo con todos esos elementos. ¿Se animan a construir su tabla de multiplicación?). Sus descubridores fueron el alemán Bernd Fischer (en cuyo haber tiene otros cuatro grupos esporádicos distintos) y el norteamericano Robert Griess. Lo descubrieron mientras se hallaban buscando otro grupo esporádico más pequeño, el ahora conocido como grupo Baby Monster (B o F2; tiene orden aproximado de un cuatro seguido de treinta y tres ceros). El grupo monstruo encierra muchas sorpresas. Entre ellas que 20 de esos 26 grupos esporádicos son subgrupos del grupo monstruo. Griess los bautizó como “la familia feliz”, mientras que los otros 6 al margen del grupo monstruo los llamó “los parias”, y así es como coloquialmente son referidos. El grupo de O’Nan es uno de esos parias, descrito por el matemático Michael Ernest O'Nan (falleció el pasado 31 de julio), aunque construido finalmente por el norteamericano Charles Sims. Teoría de las locuras monstruosas Finalmente, antes de pasar ya a explicar la noticia origen de esta reseña, expliquemos qué es la teoría de las locuras monstruosas (en inglés monstrous moonshine, o moonshine theory; no he visto traducción alguna de estos términos en español, así que me aventuro a dar ésta, explicando un poco el porqué). En 1978, el matemático John McKay estaba trabajando en funciones modulares (un campo que explicaremos en otra ocasión, pero que no tiene nada que ver con la teoría de grupos). Haciendo el desarrollo de Fourier (la expresión de una función periódica en suma de senos y cosenos) de una función modular denominada la función j de Klein, obtuvo esta expresión
McKay comentó entonces lo curioso que era que el coeficiente de q (o sea, 196884), es justamente una unidad más que el grado de la representación compleja más pequeña del grupo monstruo (que es 196883). A Conway no se le ocurrió otra cosa que responder que eso era moonshine, una expresión americana para indicar locura, idea absurda. La expresión les debió parecer ingeniosa, dando lugar a la moonshine theory, que se refiere a todo lo relativo a la inesperada relación que existe entre el grupo monstruo M y las funciones modulares, campo que ha resultado bastante fértil en cuanto a investigadores que se dedican a él y resultados obtenidos (hasta ha permitido conseguir una medalla Fields a algún matemático). Curvas elípticas ¿Y los donuts de la foto inicial? Los donuts se “asemejan” a la forma de las curvas elípticas, y en éstas interesa mucho conocer aquellos puntos de coordenadas racionales (recuérdese la reseña sobre la Conjetura de Birch y Swinnerton-Dyer) representados por esas virutas de colores. La noticia informa de que estos expertos en teoría de números han descubierto que el grupo esporádico de O’Nan almacena información relevante sobre los puntos racionales de las curvas elípticas, y puede proporcionar procedimientos para encontrarlos. Lo destacable del asunto desde el punto de vista matemático es que los grupos esporádicos hasta este momento eran entes absolutamente teóricos, sin aplicación práctica alguna conocida. Y, además, de una parcela de las matemáticas completamente diferente a la de las curvas elípticas. Volviendo a las analogías, en un donut real, se percibe perfectamente donde están los confites. Sin embargo, si estuviéramos a oscuras no lo sabríamos sin tocarlo. Eso es lo que pasa con las curvas elípticas, que no sabemos dónde están dispuestos esos dulces (los puntos racionales), pero probablemente gracias al grupo de O’Nan sea más fácil descubrirlos. Ken Ono trabaja en curvas elípticas, teoría de particiones, teoría algebraica de números, formas modulares y automórficas, y combinatoria. A modo de síntesis para no especialistas, digamos que son subramas de una de las partes más abstractas y teóricas de las matemáticas, la teoría de números. Desde los años setenta del siglo pasado aproximadamente a la actualidad han cobrado mucho interés por sus aplicaciones en criptografía (de plena actualidad en casi todas las menciones a las matemáticas de los medios de comunicación, dada su importancia en la seguridad de transmisión de mensajes y operaciones comerciales a través de internet, las comunicaciones, las tarjetas de crédito, etc.). Recientemente, Ken Ono ha estado involucrado en el asesoramiento y producción de la película El hombre que conocía el infinito (Matt Brown, EE. UU., 2015) que como recordarán recreaba la estancia en Cambridge del célebre matemático indio Srinivasa Ramanujan, otra gran figura en teoría de números. Alfonso J. Población Sáez es profesor de la Universidad de Valladolid y miembro de la Comisión de divulgación de la RSME. El ABCDARIO DE LAS MATEMÁTICAS es una sección que surge de la colaboración con la Comisión de Divulgación de la Real Sociedad Matemática Española (RSME) |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |