Las matemáticas escondidas detrás de las pinturas de Jackson Pollock
Las matemáticas escondidas detrás de las pinturas de Jackson Pollock |
 |
 |
 |
|
ABC, 18 de Diciembre de 2017 El trabajo del genial artista consistía en estructruas fractales, ciertos patrones que se repiten una y otra vez en varios niveles
Jackson Pollock, trabajando en su estudio - Archivo El nombre y, en parte, el concepto de fractal es quizás uno de los más conocidos de las matemáticas recientes por las personas ajenas a las matemáticas. Se utiliza en el análisis de situaciones muy diversas. Hoy aquí nos vamos a referir a su relación con el trabajo de uno de los pintores contemporáneos más reconocidos: Jackson Pollock. La palabra fractal aparece por primera vez en 1975, cuando B. Mandelbrot (1924-2010) publicó ‘Les objets fractales: Forme, hasard et dimension’, en cuya introducción decía: ‘El concepto que hace de hilo conductor será designado por uno de los dos neologismos sinónimos objeto fractal y fractal, términos que he inventado (…) a partir del adjetivo latino fractus,...’. Más tarde Mandelbrot propuso la siguiente definición: ‘Un fractal es un conjunto cuya dimensión de Hausdorff-Besicovitch es estrictamente mayor que su dimensión topológica’. Para situar esa definición, recordemos que los objetos geométricos ‘clásicos’, esos que se estudian en la escuela, tienen dimensiones enteras: 0 el punto, 1 la recta, 2 el plano, 3 el espacio. En los fractales se define su ‘dimensión fractal’ que es un número decimal, lo que nos conecta con el origen de la palabra. Al estar situada entre dos números enteros, no se pueden tratar como un volumen o un área normales. Si la dimensión fractal está entre 0 y 1, es un conjunto de puntos alineados que no llega a constituir una recta, a pesar de ser infinitos y estar infinitamente próximos entre sí, como pasa en el llamado ‘conjunto de Cantor’, que se puede construir haciendo los siguientes pasos: 1.- Se toma el intervalo [0, 1]. 2.- Se quita su tercio interior: el intervalo abierto (1/3; 2/3). 3.- Se quita a los dos segmentos restantes sus respectivos tercios interiores: los intervalos abiertos (1/9; 2/9) y (7/9; 8/9). Siguientes.- Se quita el tercio interior de todos los intervalos que quedan. El proceso no tiene fin.
Conjunto de Cantor-Wikipedia
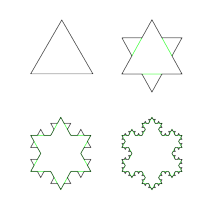
Un fractal con dimensión mayor que 1 y menor que 2 es una superficie no delimitada por una curva o un conjunto de rectas, pero que no llega a ser un plano (su perímetro es infinito y no tiene derivada en ningún punto). Un ejemplo es el fractal de Koch (también llamado ‘copo de nieve’ por su forma) que se obtiene de forma similar al anterior, pero partiendo de un triángulo equilátero y en el espacio vacío se dibuja un triángulo equilátero de ese lado, y se continúa el proceso de forma indefinida. Una de las características de los fractales es la autosimilitud, el hecho de que se tenga la misma figura, la misma representación, al aumentar o reducir la escala. Que si hacemos una foto (o una imagen en una impresora) la forma es siempre la misma si la hacemos de cerca o de lejos (o que aunque vayamos haciendo funcionar el zoom la imagen que vemos es siempre la misma). Un artista fractal Jackson Pollock (1912-1956) creador del expresionismo abstracto, es una de las grandes figuras internacionales del arte contemporáneo, desde cualquier punto de vista que se contemple. Y en uno de los más mediáticos, sus obras alcanzan cifras multimillonarias en las subastas (se dice que su cuadro "Nº 5", de 1948, fue vendido en 2006 por 140 millones de dólares).
Usaba grandes lienzos, en general colocados en el suelo, en los que aplicaba la técnica del 'drip and splash' (goteo y rociadura), una técnica poco ortodoxa pero que ha sido reconocida como un avance crucial en la evolución del arte moderno. En 1999 los científicos australianos Richard P. Taylor, Adam P. Micolich y David Jonas publicaron un artículo en la revista ‘Nature’ (‘Fractal analysis of Pollock's drip paintings’), donde mostraban que sus pinturas respetaban el principio de autosimilitud y que sus cuadros tenían estructuras fractales, generadas por cómo escurría la pintura y por la configuración geométrica que seguían los regueros que lanzaba el pintor en sus recorridos alrededor del cuadro. Calcularon la dimensión fractal de sus cuadros y vieron que desde poco mayores de 1 a mediados de los 40 fue aumentando de manera regular hasta llegar en 1952 a cerca de 1,7 en los patrones caóticos generados y de 1,9 para la dimensión de las configuraciones caóticas.
«Mural» (1943), de Pollock-Archivo El hecho de tener estructuras fractales y el crecimiento regular de su dimensión sirve para identificar e incluso para datar las obras de Pollock. En 2005 la Fundación Pollock-Krasner encargó un análisis fractal sobre unas pinturas encontradas en Nueva York que podían ser suyas. R. Taylor identificó "desviaciones significativas de las características de Pollock", aunque advirtió que los resultados deberían "combinarse con otra información importante como procedencia, conocimientos y análisis de materiales". Dos años más tarde, los científicos de materiales mostraron que los pigmentos utilizados en las pinturas eran posteriores a la muerte de Pollock. Y en 2015 el informático L. Shamir demostró que, cuando se combina con otros parámetros de patrones, el análisis fractal se puede utilizar para distinguir entre pollocks reales e imitaciones con el 93% de precisión. Si alguien quiere ver ‘en directo’ un cuadro de gran tamaño de Pollock puede acercarse al Museo Thyssen de Madrid, y en él encontrará ‘Marrón y plata I’ pintado hacia 1951 (o acceder al mismo en la web del museo). Como corresponde al hecho de ser una de las obras de la última etapa del artista, su dimensión fractal es grande, aproximadamente 1.70. Mandelbrot decía que "las nubes no son esferas, las montañas no son conos, las costas no son círculos, y las cortezas de los árboles no son lisas, ni los relámpagos viajan en una línea recta", mientras que Pollock confesaba que “los ritmos de la naturaleza son los que me importan”. No es extraño por tanto que, de una forma intuitiva y sin ser consciente de hacerlo, construyera estructuras fractales para representarlos: estamos ante un gran artista fractal. Fernando Corbalán. Universidad de Zaragoza. Miembro de la Comisión de divulgación de la Comisión de Divulgación de la Real Sociedad Matemática Española (RSME). El ABCDARIO DE LAS MATEMÁTICAS es una sección que surge de la colaboración con la Comisión de Divulgación de la Real Sociedad Matemática Española (RSME) |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |