La cicloide, la curva más rápida posible
La cicloide, la curva más rápida posible |
 |
 |
 |
|
ABC, 6 de Marzo de 2018 En «La vida es una curva (I)» el matemático Fernando Corbalán escribe sobre una curiosa línea que es braquistócrona, en la que el tiempo de descenso es mínimo, y tautócrona, en la que el tiempo de llegada no depende de la altura
Un cicloide en una pista para actividades deportivas - WIKIPEDIA Hace muchos años, una canción famosa afirmaba «La vida es una tómbola». Yo más bien creo que podemos utilizar la misma tonadilla para proclamar: «La vida es una curva». Y no solo por aquello de que la estructura de la vida está inscrita en la doble hélice del ADN, sino porque, por más que se empeñen las matemáticas y la civilización en encontrar rectas y ángulos rectos, lo que vemos a nuestro alrededor es más curvo que recto. Con el añadido de una tendencia personal hacia las curvas, que comparto con el gran arquitecto Oscar Niemeier («No es el ángulo recto lo que me atrae,/ni la línea recta,/dura, inflexible creada por el hombre./Lo que me atrae es la curva libre y sensual») y el poeta Jesús Lizano («Mi madre decía: a mí me gustan las personas rectas./A mí me gustan las personas curvas,/las ideas curvas,/los caminos curvos,/porque el mundo es curvo/y la Tierra es curva/ y el movimiento es curvo»). Por eso iniciamos con la cicloide una serie sobre algunas curvas especiales y sus peculiaridades. El movimiento de un punto en una rueda Vamos a pensar en una circunferencia que gira sin resbalar y un punto fijo de ella. Al dar una vuelta completa, ¿qué curva traza ese punto? A bote pronto parece que es fácil la respuesta: es también una circunferencia. Pero una vez más la evidencia nos juega malas pasadas. Así es que para visualizarla miramos la rueda de una bicicleta y nos fijamos en la trayectoria que recorre la válvula que se utiliza para hincharla. La curva que resulta, que no es una circunferencia, y que se ve en la figura, se llama cicloide.
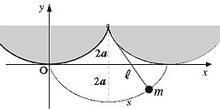
Trayectoria de un punto fijo en una circunferencia que gira sin resbalar Una curva de origen tan poco sofisticado parece que debería tener unas propiedades muy normales, y sin embargo no es así, sino que veremos que merece una etapa de «La vida es una curva». Si nos vamos a la historia y llegamos a Johann Bernoulli (1667-1748), miembro destacado de la familia con más matemáticos brillantes, que en 1696 propuso a la comunidad el reto de encontrar la curva del descenso rápido. Es decir: «Entre las infinitas curvas que unen los dos puntos dados o que pueden dibujarse del uno al otro, elegir una tal que si la curva se reemplaza por un tubo delgado o ranura en los que se coloca una pequeña esfera y se deja caer, entonces esta esfera pasaría de un punto al otro en el tiempo más breve posible». Destaquemos que no se trata de longitud mínima (en cuyo caso sería una recta), sino del tiempo mínimo en pasar de uno a otro, lo que le da un gran valor por la optimización de la movilidad. Varias mentes brillantes de la pequeña comunidad matemática propusieron cinco soluciones al reto que coincidían en dar la cicloide como respuesta. Además de las del propio autor del desafío, entre estas estaban las de su hermano mayor, Jacob Bernoulli (1655-1705), Leibnitz (1646-1716), L’Hôpital (1661-1704) y Newton (1643-1727). Con este problema, esta constelación de talentos hacían nacer el cálculo de las variaciones, una nueva rama de las matemáticas, en la que el objetivo de los problemas no era buscar puntos de una curva con una propiedad prefijada, sino encontrar curvas (o funciones) que satisficieran una determinada propiedad. Propiedades de la cicloide La primera de ellas es la de la exigencia de Bernoulli, lo que se llama la curva braquistócrona: la de descenso más rápido entre dos puntos. Como la rapidez es una de las características de nuestro tiempo, se puede utilizar este perfil para los toboganes de los parques de atracciones; y si no siempre se hace es por las dificultades de diseño. También podemos recuperarlo si queremos hacer algún tobogán familiar. De hecho, la cicloide es en general la curva del perfil de los toboganes de patinaje (cada vez más presentes en nuestras ciudades, y que se conocen como «half») para llegar abajo de la forma más rápida. Pero la cicloide tiene otra propiedad inesperada y sorprendente, la tautocronía, que significa que si un móvil se desplaza a lo largo de la curva, en caída libre, llegará al punto más bajo de la curva en un tiempo que no depende de la altura del punto de salida. Esto se puede visualizar colocando dos cicloides iguales enfrentados y dejando caer dos bolas, cada una desde un punto cualquiera de cada una de las cicloides y comprobando que llegan las dos a la vez al punto más bajo en que se juntan las cicloides. Esa propiedad fue utilizada por el astrónomo holandés Huygens (1629-95) en 1673, en su obra «Horologium Oscillatorum», para la construcción de péndulos, que permitían obtener relojes exactos (un problema hoy menor, puesto que hay relojes incorporados a la inmensa mayoría de aparatos que utilizamos, pero que ha supuesto un desafío importante para la humanidad a lo largo de la historia). El péndulo cicloidal de Huygens El péndulo cicloidal que propuso Huygens tiene el hilo suspendido el entre dos contornos sólidos con la forma de arcos de cicloide tangentes en su punto de unión. Al oscilar el péndulo, el hilo va de uno a otro de esos dos contornos, y la longitud del péndulo queda disminuida en una proporción que depende de la amplitud de las oscilaciones. Huygens mostró que si la circunferencia que genera los dos contornos cicloidales tiene un radio la cuarta parte de la longitud del hilo del péndulo entonces la masa del péndulo describe un arco de cicloide cuya circunferencia generatriz tiene el mismo radio. Y así se tiene un péndulo cuyas oscilaciones son exactamente iguales, es decir un péndulo isócrono, que permite construir relojes precisos.
De esta forma se pudo comenzar a resolver un problema muy importante para la navegación: la determinación precisa de la longitud del lugar en que se encontraban (la otra coordenada, la latitud podía conocerse con medidas astronómicas). Problema que fue objeto de ofertas de recompensas importantes por parte de las autoridades inglesas, y que no fue resuelto satisfactoriamente hasta un siglo después, por medio del cronómetro marino de John Harrison. Área y longitud También la longitud de la cicloide y el área que limita (en una vuelta de la circunferencia) tienen unos valores sorprendentes. La longitud L de la cicloide, contra lo que sería esperable, no depende de π y es igual a ocho veces el radio r de la circunferencia que la engendra:
En cuanto al área A que limita la cicloide con la recta de desplazamiento del círculo de radio r que la genera es el triple del área de ese círculo:
O sea que si ponemos dentro de la figura de la cicloide el círculo que lo genera, resulta que las tres partes que hemos marcado tienen la misma superficie.
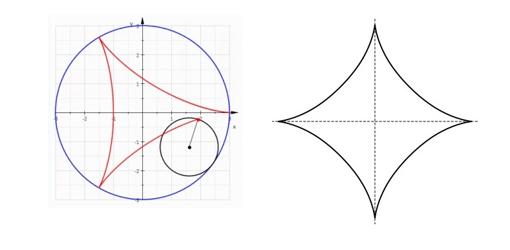
Las hipocicloides Anterior en el tiempo (puesto que ya Cardano las describió en su libro «De proportionibus» en 1570) y relacionadas con la cicloide son las hipocicloides. Una hipocicloide es la curva que describe la trayectoria de un punto situado en una circunferencia (llamada generatriz) de radio r que rueda sin deslizarse por el interior de otra circunferencia (llamada directriz) radio R (siendo r menor que R). Según la relación entre los radios de las dos circunferencias se tiene una familia de curvas. En los casos en que el cociente entre los radios n=R/r es entero, la hipocicloide obtenida se cierra al cabo de una vuelta, y tiene n cúspides o «vértices». Cuando n =3 se llama deltoide (porque es parecida a la letra delta, y se emplea en ingeniería mecánica) y si n = 4 la curva se llama astroide.
Un deltoide (izquierda) junto a un astroide (derecha)-WIKIPEDIA Y para terminar con esta primera entrega de «La vida es una curva» una reflexión sobre ambos temas de Javier Enríquez Serralde: «La vida es una curva larga que no avanza cuando la quieres acelerar, se precipita cuando la quieres frenar y termina sin que te des cuenta». Fernando Corbalán. Universidad de Zaragoza. Miembro de la Comisión de divulgación de la Real Sociedad Matemática Española (RSME). El ABCDARIO DE LAS MATEMÁTICAS es una sección que surge de la colaboración con la Comisión de Divulgación de la Real Sociedad Matemática Española (RSME) |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |