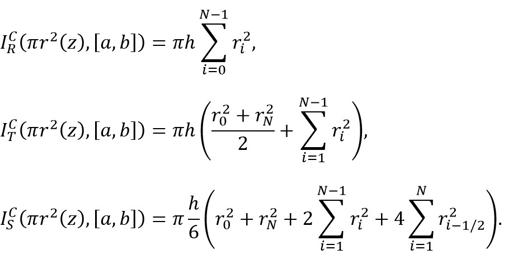Los secretos de la cultura vaccea, al descubierto gracias a las matemáticas
Los secretos de la cultura vaccea, al descubierto gracias a las matemáticas |
 |
 |
 |
|
ABC, 10 de Diciembre de 2018 Diferentes teoremas permiten reconstruir elementos tan importantes de esta sociedad prerromana como las vasijas y los recipientes rituales
Yacimiento vacceo de Pintia, en Valladolid - ICAL El estudio de volúmenes en piezas arqueológicas tiene interés para investigar la existencia de medidas de capacidad estandarizadas, así como para inferir datos de manejabilidad, frecuencia de utilización, tasa de reemplazo, funcionalidad, etc. La forma habitual de calcular el volumen de vasijas encontradas en yacimientos es rellenar el recipiente con agua o, si la pieza es porosa o frágil, con semillas, y después trasvasar el contenido a una probeta graduada. Sin embargo, calcular de esta manera la capacidad de los recipientes recuperados de las excavaciones tiene varias dificultades. Por ejemplo, no siempre es posible completar el puzle a partir de las piezas rescatadas; o las vasijas son demasiado grandes, o delicadas; o es complicado acceder a los materiales originales conservados en los museos (necesidad de permisos, almacenaje poco adecuado, etc.). Por eso, a veces la única información que se maneja es la que aparece en las publicaciones. Pero las matemáticas pueden proporcionar un método para estimar la capacidad de aquellas piezas para las que no es posible comprobar su volumen de forma material. Para ello se puede aprovechar el hecho de que, como parte del estudio de las piezas encontradas en las excavaciones, se hace de forma sistemática el dibujo de una sección del recipiente a escala. En el caso de las piezas torneadas (o en lenguaje matemático, figuras de revolución que se generan girando una curva plana alrededor de un eje), conocer la sección de la pieza es suficiente para calcular su volumen, o al menos aproximarlo con bastante precisión. El Teorema de Fubini La forma general de calcular el volumen de un conjunto acotado de tres dimensiones es calcular la integral triple sobre dicho conjunto de la función uno. Esta integral triple se reduce a una integral de una dimensión cuando se conoce el área de las secciones del conjunto sobre uno de los ejes, aplicando el Teorema de Fubini a este caso particular. En los cuerpos de revolución las secciones son círculos y, por tanto, tienen área conocida en función del radio (recordamos de la escuela: pi multiplicado por el cuadrado del radio), que, en el caso de vasijas, en general es variable con la altura (porque si fuera idéntico, tendríamos un tubo, un cilindro, y los pueblos antiguos tenían cierta estética artística). De este modo, el volumen de un cuerpo de revolución alrededor del eje z, con radio r(z) entre las alturas a y b viene dado por:
Conociendo entonces el radio en función de la altura, evaluaríamos la integral calculando una primitiva del radio al cuadrado y aplicando la regla de Barrow. El problema es que, a partir del dibujo de la sección de la pieza, no tenemos la expresión analítica de la función del radio y, por tanto, no podemos calcular la primitiva correspondiente. En este caso, podemos recurrir a una fórmula de cuadratura numérica utilizando una tabla de valores de la función que obtendremos midiendo los radios de la vasija a distintas alturas y calculando después una combinación lineal de estos valores. Por ejemplo, podemos usar la regla del rectángulo compuesta, la regla del trapecio compuesta y la regla de Simpson compuesta con espaciado fijo, cuya convergencia para funciones suficientemente regulares es lineal, cuadrática y cuártica respectivamente. Aunque esto parezca muy técnico, el procedimiento no es complicado: En primer lugar, dividimos la altura (que como se ha dicho, está representada en un intervalo [a, b]) en N partes iguales (5, 10, 200, las que queramos; en matemáticas utilizamos un valor general N, que luego sustituimos por un número concreto). La longitud de cada una de las partes en que queda dividida la altura (todas iguales porque las hemos tomado así) se llama equiespaciado, y lo representamos por la letra h. Su expresión no es difícil de entender: h = (b − a)/N. A los extremos de cada división se les denomina nodos, y tendrán la expresión zi = a + i h, con i variando desde 0 hasta N. El radio en cada uno de esos nodos es r(zi) = ri, y ri−1/2 representará el radio en los puntos medios de los subintervalos. Las reglas compuestas del rectángulo, trapecio y Simpson tienen respectivamente las siguientes expresiones:
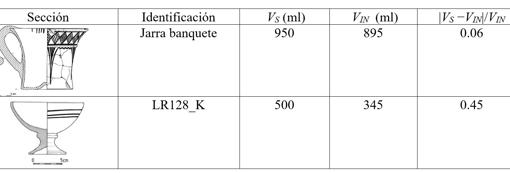
Cuando el tamaño h del espaciado con el que se miden los radios se hace muy pequeño (tiende hacia cero, en jerga matemática), los errores de cuadratura también tienden a cero, pero además cuanto mayor es el orden de convergencia más rápidamente convergen a cero los errores. Para validar el procedimiento proponemos comparar el volumen medido con el método físico de llenado con semillas y probeta graduada (VS), y el volumen calculado con los métodos de integración numérica (VIN) descritos previamente, utilizando la cerámica del yacimiento vacceo de las Quintanas, de Padilla de Duero, situado a cuatro kilómetros de Peñafiel, cuyo Centro de Estudios Vacceos Federico Watemberg (CEVFW) pertenece a la Universidad de Valladolid. En el estudio hemos utilizado, entre otros, algunos de los materiales encontrados en la campaña del año 2003 dentro de la llamada «estancia del banquete», de la casa 4 del nivel sertoriano que corresponde al primer tercio del siglo I a.C. Posibles errores en las mediciones De todas las fuentes de error que pueden aparecer al calcular el volumen de la forma propuesta, la principal es la que tiene que ver con posibles deformaciones de la pieza. La manipulación del alfarero o fallos en la cocción pueden hacer que no sea de revolución perfecta. Cuando el dibujante toma la pieza artesana y dibuja su sección, si la pieza no es muy irregular, el principal error será el que cometa con el conjunto discreto de medidas que tome, pero si además la pieza está bastante deformada, dependiendo del ángulo que considere para hacer la sección, puede haber bastante diferencia entre una sección y otra. En la Tabla 1 se muestran dos de las piezas consideradas, junto con su volumen VS , su volumen VIN y el error relativo |VS −VIN|/VIN para así poder comparar errores de distintos recipientes.
Volúmenes VS y VIN y error relativo |VS −VIN|/VIN para dos de las piezas Como se puede ver en la Tabla 1, en el caso de la jarra del banquete la aproximación obtenida tiene un error relativo del 6%, que podemos considerar aceptable. Sin embargo, para la pieza LR128_K se obtiene una aproximación con un error relativo del 45%, lo que nos hace desechar la aproximación. La razón de un resultado tan dispar para la copa LR128_K podemos encontrarla en una foto cenital de dicha pieza que presentamos en la Imagen 3, en la que se observa claramente la deformación de la copa, especialmente en el cuarto superior derecho. Probablemente la sección de esta pieza se ha hecho desde algún ángulo de esa zona con un radio menor, por lo cual el volumen calculado con la sección queda por debajo del volumen medido físicamente con semillas.
Vista cenital de la copa LR128_K Volviendo a la cuestión inicial de si podemos calcular el volumen de una pieza arqueológica cuya única información es la sección, acompañada de la escala, concluimos que depende de la regularidad de la pieza. Si el recipiente tiene una deformación, por ejemplo, debida a una cocción deficiente, las secciones dejan de ser círculos y serán otras figuras ovaladas, probablemente diferentes en cada altura, con lo que la fórmula utilizada para calcular el volumen ya no es válida y da lugar a un error considerable. Por tanto, es necesario conocer la regularidad de la pieza para asegurarse de que el error de la estimación propuesta sea aceptable. Más información acerca del procedimiento aquí. -Páginas 91−93 de Vaccea Anuario, nº11 (2017)- Ana María Portillo de la Fuente es miembro del IMUVA y profesora del Departamento de Matemática Aplicada de la Universidad de Valladolid. El ABCDARIO DE LAS MATEMÁTICAS es una sección que surge de la colaboración con la Comisión de Divulgación de la Real Sociedad Matemática Española (RSME) |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |