 El problema sin solución al que ha llevado la inteligencia artificial
El problema sin solución al que ha llevado la inteligencia artificial |
 |
 |
 |
|
ABC, 14 de Enero de 2019 ¿Qué relación existe entre Pigmalión, Alan Turing, Blade Runner y la hipótesis del continuo? Seguramente algún lector podrá establecer alguna entre algún par de ellos, pero, ¿entre todos? Confiemos en que tras leer esta no elemental reseña todos acaben descubriendo las claves del acertijo
Gödel está considerado el matematico más influyente del siglo XX, famoso por sus teoremas de incompletitud - Archivo / Vídeo: El 80% de las compañías utilizará inteligencia artificial en 2020 Las matemáticas y sus investigadores no paran. A la vuelta de las vacaciones navideñas encontramos en medios internacionales la noticia de que la capacidad de aprendizaje puede ser un problema indecidible. Dicho así seguramente nadie entenderá de qué va el asunto, salvo algunos matemáticos, y por supuesto los especialistas en lógica, de modo que tratemos de desgranar un poco dicha afirmación que además no asegura nada concreto (“puede ser”, pero quizá no; no se sabe). Si ustedes estudiaron la Enseñanza General Básica (EGB) recordarán que desde los seis años los libros de matemáticas que manejaban estaban repletos de unos entes llamados conjuntos, representados mediante una especie de contorno cerrado de variadas formas, que contenían, o no, todo tipo de figuras más pequeñas (geométricas de colores, o símbolos, u objetos reales) llamadas elementos. Alguno todavía soñará con uniones, intersecciones, complementarios, inclusiones, pertenencias y demás ideas que acabó manejando a duras penas pero que nunca entendió para qué servía nada de aquello. Fue la llamada matemática moderna, que se introdujo en nuestro sistema escolar siguiendo los pasos del grupo francés Bourbaki (en realidad tenía el nombre de una persona, Nicholas Bourbaki, sujeto que luego supimos que nunca existió, sino que era un conjunto, de nuevo la palabreja, de matemáticos que se propusieron la tarea de presentar todas las matemáticas conocidas de un modo ordenado y lógico). Los que continuamos estudiando carreras universitarias más teóricas, acabamos entendiendo un poco (nunca se puede estar seguro de todo al cien por cien) de qué iba todo aquello. Ya Euclides, sobre el 300 antes de Cristo, recopiló y ordenó toda la matemática conocida en aquel momento (Geometría en su mayor parte) en trece volúmenes conocidos como Los Elementos (el tratado más leído y traducido de la Historia después de La Biblia, lo cual tiene su mérito, no me lo negarán). Eligió como procedimiento disponerlo en una serie de secciones fijas: axiomas (cinco principios básicos incuestionables por su elementalidad, salvo uno más discutido, sobre los que se basa todo), definiciones, proposiciones y sus demostraciones (basadas en argumentos lógicos y/o en resultados demostrados previamente). Ninguno de estos últimos ha sido jamás rebatido desde que se comprobara que la demostración era correcta. Por eso la matemática es la herramienta más poderosa y exacta que ha concebido el ser humano, por el momento. Pero algunos asuntos no estaban tan claros como otros. Por ejemplo, las paradojas (enunciados que razonados de modos distintos nos llevan a conclusiones opuestas) o los inconmensurables (los números que hoy conocemos como irracionales, no porque no se sepan qué son, que se sabe perfectamente, sino porque no son racionales, es decir, no son cociente de dos números enteros). Ideas como éstas planteaban un agujero en la perfección del sistema matemático. Los siglos pasan, la matemática avanza, se descubren muchos más resultados (los más generales e importantes los llamamos teoremas), y estos asuntos polémicos se van soslayando de uno u otro modo, a la vez que aparecen nuevas controversias con otros conceptos. Entonces llega un momento en que los matemáticos se plantean resolver definitiva y correctamente todos estos asuntos (hubo muchos intentos, pero no llegaban a conclusiones satisfactorias para todos, siempre se encontraba algún fleco). Por ejemplo, se intentó basar todo en lo más elemental y básico de las matemáticas, los números, la Aritmética. Pero, el problema del infinito lo estropeaba todo (para los que creen que esto es algo artificial y que no existe, que los hay, inexplicablemente, que intenten pensar en el número más grande que puedan, ya verán como les encontramos uno mayor simplemente diciéndoles “más uno”; vamos, que los propios números naturales son infinitos). Y aparecen los lógicos. Entre ellos, George Cantor, que hacia 1872 define la teoría de conjuntos para intentar dar una base firme a todas las matemáticas. Se trataría de organizar toda la matemática en base a unos axiomas que ahora no serían geométricos como los de Euclides, sino definiendo unas operaciones sobre los conjuntos. Entre éstas, la intersección y la unión, cuyos “análogos” algebraicos serían la multiplicación y la suma, respectivamente, junto a la idea de complementario. Aparece así el álgebra de conjuntos. Y matemáticos como Augustus De Morgan deduce leyes que los relacionan, y John Venn en 1881 crea unos diagramas para manejar los conjuntos con sencillez. Veamos un ejemplo sencillo para refrescarnos estas ideas:
A∩B = {1, 2, 4} A∪B = {1, 2, 3, 4, 5, 6, 8} ¬A = {6, 7, 8, 9} ¬B = {3, 5, 7, 9} Seguro que el lector podrá asimismo comprobar, en este ejemplo, que se verifican las leyes de De Morgan: ¬ (A∪B) = (¬A) ∩ (¬B) ¬ (A∩B) = (¬A) ∪ (¬B) Respecto a los símbolos, cuando un elemento está en un conjunto, se dice que pertenece a ese conjunto y se denota mediante ∈; si no está, se utiliza ∉. Si un conjunto está dentro de otro, se dice que está incluido en él, y se utiliza el símbolo ⊆ y si no lo está, se usa ⊄. Así en el ejemplo anterior, tenemos que 2∈A∩B, 7∉A∪B y A∪B⊆E. Todo funciona perfectamente si los conjuntos son finitos, es decir, si tienen un número finito de elementos. Pero cuando tienen una cantidad infinita, la cosa vuelve a complicarse. A todo esto, los conjuntos, no sólo se describen dando sus elementos, como en el ejemplo anterior; también pueden expresarse indicando alguna (o algunas) propiedades que los definen. Por ejemplo, A = {x∈ℤ tales que x es un número par, y x > 150} Obviamente A es el conjunto de los infinitos enteros pares mayores que 150 (o sea, A = {152, 154, 156, …}). Para complicar aún más las cosas, al matemático y filósofo Bertrand Russell se le ocurrió definir conjuntos como aquel formado por todas las cosas que no se contengan a sí mismas. En símbolos, C = {x tales que x∉x}. Este conjunto nos lleva a una paradoja cuando nos preguntamos si C∈C. Tanto respondiendo “Si”, como respondiendo “No”, se llega a una contradicción. Como los matemáticos somos conscientes de que el ciudadano de a pie se puede perder en este lenguaje, nos hemos inventado historias, como la del barbero para que traten de entenderlo bien: Imaginemos un pueblo en el que sólo hay un barbero, y no da abasto para atender a toda la población. Ante sus quejas, el alcalde decide que sólo afeite a aquellas personas que no puedan afeitarse por sí mismas. Al día siguiente a publicarse el edicto, el barbero delante del espejo se encuentra ante un dilema sin solución: yo puedo afeitarme por mi mismo porque soy un ciudadano de este pueblo y no estoy impedido; pero como soy barbero, no puedo afeitar más que a aquellos que no lo puedan hacer por sí mismos. Entonces, ¿qué hago? Otra versión es la del índice de la biblioteca. Una biblioteca con muchos libros, miles, debe tener un índice donde aparezcan todos para poder localizarlos bien. Como hay muchos, ese índice es un libro voluminoso (no hay ordenadores en esta biblioteca, qué le vamos a hacer). Por tanto, como libro que es, debe aparecer en el índice, que es el propio libro. ¿Y cómo referenciamos este libro dentro de sí mismo? ¿Dónde colocamos el volumen físicamente? Un último ejemplo. En un papel pone “Esta frase es falsa”. Si la hacemos caso, es decir, asumimos que nos da una información cierta, tenemos que es falsa. Pero por ser falsa, no deberíamos hacerla caso. Entonces, ¿la hacemos caso o no? (Menos mal que ni las compañías de seguros ni los políticos no hacen mucho caso a las matemáticas; claro que tampoco les hace falta para tomarnos el pelo, aunque puedan hacerlo por sí mismos, ja ja ja). Como vemos hay afirmaciones, conjuntos, que son indecidibles, esto es, no podemos afirmar ni que sean ciertos, ni que sean falsos. Esto lo demostró el lógico austriaco Kurt Gödel en 1931, y echó por tierra la vieja esperanza de la comunidad matemática de poder establecer un conjunto de axiomas que rigieran de un modo exacto, perfecto, toda la matemática existente y por descubrir. Se acababan de enunciar los axiomas de Zermelo-Fraenkel para la teoría de conjuntos que también los llevaron a un segundo plano respecto a ese ambicioso proyecto. Pero los matemáticos (algunos), a la vez que trabajaban en estas cosas teóricas, andaban enfrascados en cosas prácticas que se necesitaban. Concretamente un señor llamado Alan Turing, pensaba también cómo construir una máquina que fuera capaz de descifrar los mensajes codificados que transmitía, cambiando las claves diariamente, un artefacto llamado Enigma (del que no me extiendo porque ya saben de qué va la historia; en su desarrollo andaba la idea de máquina de Turing). Y más aún, iba pensando en algún procedimiento para poder determinar si, al otro lado del teléfono, o del ordenador en la actualidad, me está contestando una persona real, u otra máquina (o sea, un replicante, en términos cinéfilo-literarios). Eso le llevó a conformar el llamado test de Turing. Y poniéndose al otro lado, se planteó cómo lograr que una máquina no sea descubierta que lo es. Esto le lleva a los inicios de la conocida como inteligencia artificial. Quizá algunos conozcan un sencillo juego que se proporcionaba al adquirir alguno de los primeros ordenadores personales (recuerden, ¡¡¡juegos que funcionaban en ordenadores de 16 o 48 Kb de memoria RAM!!! Y hoy necesitan tropecientas gigas sólo para cargar el Fortnite. Si Turing levantara la cabeza…) llamado “Animal, Vegetal, Mineral”. El usuario pensaba uno de ellos, y el ordenador te hacía unas preguntas de respuestas únicas “Sí”, o “No”. Tenía en memoria un montón de animales, vegetales y minerales con una característica de cada uno. Según las respuestas, hacía unas u otras preguntas (¿recuerdan el artículo sobre redes neuronales y conducción automática? Pues este juego se basa en un modelo más sencillo de red neuronal). Si lograba adivinar el objeto pensado en menos de 20 preguntas, ganaba él; si, por el contrario, no tenía en su base de datos el objeto y ganaba el jugador, perdía y te pedía el nombre y una característica de dicho objeto. Así iba “aprendiendo”. Este ejemplo sencillo entra dentro del llamado aprendizaje automático. Otro famoso ejemplo es el programa ELIZA, desarrollado en el MIT entre 1964 y 1966 por el informático Joseph Weizenbaum. Con él pretendía mantener una conversación de texto coherente con el usuario, sin que éste se supiera que era una máquina. El nombre es un homenaje al personaje principal de una conocida obra teatral de George Bernard Shaw (con varias versiones en el cine también, por si lo prefieren). Bien, y llegamos al final. Los matemáticos Shai Ben-David, Pavel Hrubeš, Shay Moran, Amir Shpilka y Amir Yehudayoff han publicado un artículo en el que muestran que la capacidad de aprendizaje de una máquina puede ser un problema indecidible. Esto pone límites no sólo a las máquinas sino al propio ser humano. Han llegado a esta conclusión investigando la conexión entre capacidad de aprendizaje y compresión, es decir, cómo resumir las características principales de un gran conjunto de datos en un conjunto más pequeño de ellos. La forma eficiente de hacerlo se reduce a una cuestión de la teoría de conjuntos. Y más cosas, como que el problema de la capacidad de aprendizaje es equivalente a la hipótesis del continuo, uno de los enigmas sin resolver más preciados de las matemáticas (telegráficamente, ¿existe un conjunto infinito cuyo cardinal se encuentre entre el de los números naturales y el de los reales?). Si alguno se anima a trabajar en este tipo de problemas lógicos (ganará mucho dinero si consigue algo destacable), un consejo: repasen primero cómo acabaron casi todos los especialistas aquí mencionados: Cantor, Gödel, Turing, …. Para contrarrestar, mírense también algo de Russell. Alfonso J. Población Sáez es profesor de la Universidad de Valladolid y miembro de la Comisión de divulgación de la RSME. El ABCDARIO DE LAS MATEMÁTICAS es una sección que surge de la colaboración con la Comisión de Divulgación de la Real Sociedad Matemática Española (RSME) |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |







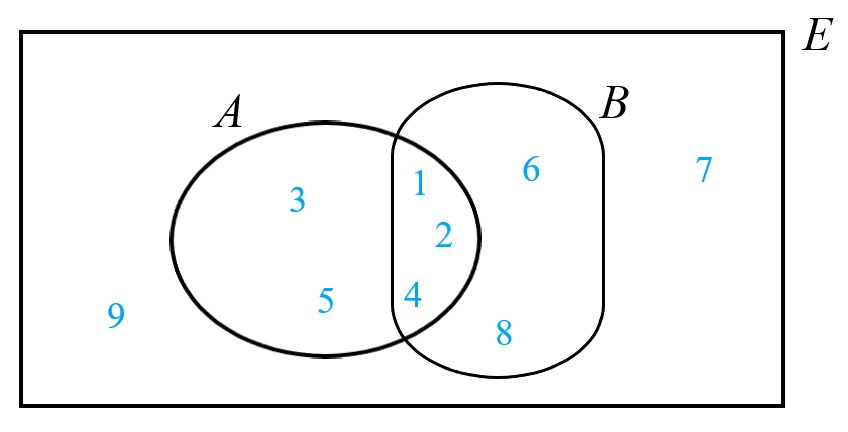 Sean los conjuntos A = {1, 2, 3, 4, 5}, B = {1, 2, 4, 6, 8} y E = {1, 2, 3, 4, 5, 6, 7, 8, 9}. La intersección (los elementos que están a la vez en A y en B) la denotamos mediante el símbolo ∩, la unión (elementos que están en A o en B) la denotamos mediante ∪ y el complementario (elementos que están fuera de un conjunto) mediante ¬. Entonces, ayudándonos del diagrama de Venn de la imagen, es sencillo comprobar que
Sean los conjuntos A = {1, 2, 3, 4, 5}, B = {1, 2, 4, 6, 8} y E = {1, 2, 3, 4, 5, 6, 7, 8, 9}. La intersección (los elementos que están a la vez en A y en B) la denotamos mediante el símbolo ∩, la unión (elementos que están en A o en B) la denotamos mediante ∪ y el complementario (elementos que están fuera de un conjunto) mediante ¬. Entonces, ayudándonos del diagrama de Venn de la imagen, es sencillo comprobar que