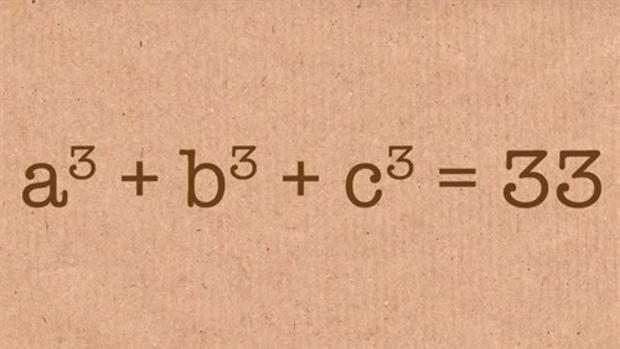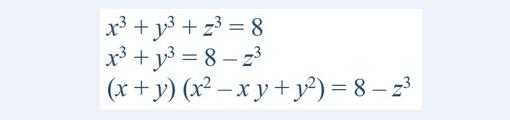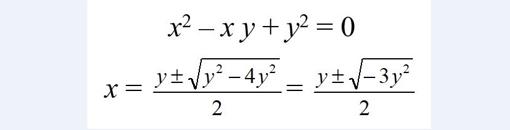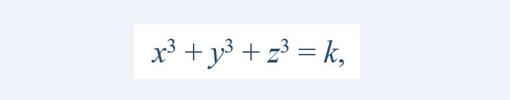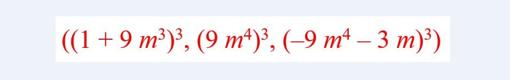Solucionan el diabólico acertijo matemático que no ha podido ser resuelto en 64 años
Solucionan el diabólico acertijo matemático que no ha podido ser resuelto en 64 años |
 |
 |
 |
|
ABC, 8 de Abril de 2019 El reto con el 33 ha sido descifrado por Andrew Bookerm, de la Universidad de Bristol
Problema matemático resuelto el pasado mes de marzo - YouTube Hace un par de semanas, nuestro compañero Pedro Alegría nos hablaba sobre la posibilidad de descomponer números enteros como suma de cuadrados, de cubos, etc., tirando del hilo del teorema de Pitágoras o del último teorema de Fermat (en ellos es únicamente con dos sumandos, pero nada nos impide hacerlo con más (problema de Waring). Hace unos días ha sido noticia un resultado relacionado, en el que un matemático británico (abstrayéndose del no menos difícil problema del « Brexit») daba a conocer que había encontrado una solución a un asunto planteado hace mucho tiempo (unos cuantos siglos nada más). Seguramente ustedes no se lo hayan planteado, pero no sé si sabrán que, si tienen un cubo (imagínense un terrón de azúcar, una caja de cartón de lados cuadrados, o un simple cubo de Rubik) pongamos que de 2 unidades de lado (o sea con un volumen de 8 unidades cúbicas), es imposible dividirlo en otros dos cubos más pequeños cuya suma de volúmenes sea la inicial, 8. En términos numéricos, si 8 = x³ + y³, no se pueden encontrar valores enteros para x, y que verifiquen la ecuación. Eso es lo que dice el último teorema de Fermat en el caso de exponente cúbico. Vale, está demostrado (Andrew Wiles lo hizo) que no se puede. Pero, ¿y si lo quiero poner como suma de tres cubos? Es decir, ¿existen valores enteros x, y, z tales que x³ + y³ + z³ = 8? Como 8 es un cubo (2³), aunque no es una solución muy elegante, seguramente alguno de ustedes diga: Fácil, 0³ + 0³ + 2³ = 8. Incluso, algunos otros vayan un poco más allá y se hayan percatado de que a³ + (–a)³ + 2³ = 8 también, sea quien sea el entero a. Para un matemático esto no es más que un ejemplo obtenido casualmente; necesita saber por qué, y si hay algún otro caso particular semejante. Esto no le resulta demasiado complicado:
Es decir que el factor (x + y) es un divisor del segundo miembro 8 – z³, y por tanto cuando es cero (es decir, cuando z = 2), la igualdad se cumple si x + y = 0, que es lo mismo que decir que y = –x. Por tanto, la tripleta (x, –x, 2) resuelve la cuestión que habíamos encontrado “a ojo”. El otro factor, x² – x y + y², no sirve porque sólo es nulo cuando una de las variables es un número complejo, y sólo nos interesan valores enteros. Para verificarlo no tienen más que intentar resolverlo con la conocida fórmula que nos enseñaron en la escuela de las ecuaciones de segundo grado (tomando x como incógnita, e y como constante):
Como y² es siempre un número positivo, –3 y² es negativo, y la raíz cuadrada de un número negativo se interna en el campo de los números complejos. Pero los matemáticos no perdemos el tiempo para resolver una sencilla ecuación como esa. Ya que nos molestamos, tratamos de resolver si existen valores enteros x, y, z que verifiquen la ecuación
Siendo k cualquier número entero. Cualquiera (y como saben existen infinitos). ADVERTENCIA MATEMÁTICA Para los que se pregunten que para qué sirve hacer eso, no se molesten en reiterarlo en los comentarios. Nadie pone reparos en decir que para qué sirve componer una oda al mar (cuando ya lo vemos con nuestros propios ojitos), o una estupenda canción, o escribir un maravilloso libro sobre cosas que no existen ni existirán (como gnomos, elfos, o cosas similares), o filosofar sobre lo humano y lo divino (lo humano existe, lo divino está por ver, pero en cuestiones de fe no nos metemos), etc., etc. Disfrutamos con ello, es parte de la cultura. Pues las matemáticas, la ciencia, también. Con la pequeña diferencia de que, a veces, resultados que se demostraron en el pasado, y que entonces sólo servían para poner a prueba el ingenio y la inteligencia de sus coetáneos, siglos después han tenido aplicaciones y usos fundamentales para nuestras vidas (¿hace falta que vuelva a recordarles que si duermen tranquilos cuando toda persona viviente es capaz de conocer los números de sus cuentas bancarias o de sus tarjetas de crédito es porque hay unos datos encriptados a los que no pueden acceder, y que esa encriptación se debe a resultados matemáticos de la teoría de números, la rama de las matemáticas de la que hablamos hoy?). Por tanto, los teoremas y resultados matemáticos que hoy demostramos, totalmente teóricos, quizá algún día (si no nos cargamos todo antes) puedan servirles a los ciudadanos del futuro. Se los legamos desinteresadamente. Lo primero que nos preguntamos los matemáticos para tratar de resolver esa ecuación, x³ + y³ + z³ = k, es cómo deben ser esos valores k. Dicho de otro modo, si sumamos tres enteros al cubo, ¿qué tipo de valores nos van a dar? ¿Nos pueden dar todos los enteros? ¿Sólo algunos? ¿Ninguno? O sea, vamos a intentar averiguar cómo es la suma de tres enteros al cubo. Empecemos por uno sólo. ¿Cómo resulta ser un número elevado al cubo? Luego ya veremos la suma de tres de ellos. Algunos conceptos sencillos En este momento es necesario recordar algunos conceptos sencillos de teoría de números, alguno de los cuales les puede ayudar a hacer cálculos mentales rápidamente. Uno de ellos es una herramienta para conocer el resto de la división por un número, ¡¡¡sin hacer la división!!! Bueno, eso quizá sea poner las expectativas muy altas. Digamos, saber el resto de la división por algunos números, ¡¡¡sin hacer la división!!! Por ejemplo, la división entre 9 nos proporciona mucha información para esto de la suma de cubos. El 9 posee propiedades interesantes, como el de la raíz digital de un número. Tenemos un número expresado en base decimal, por ejemplo, el 123456789 (pon poner un numerillo que no quepa en las calculadoras). Sumamos sus dígitos entre sí, es decir, 1+2+3+4+5+6+7+8+9. Nos da 45. Volvemos a hacer lo mismo, hasta que nos quede un solo dígito. En este caso, 4+5=9. Ese valor es la raíz digital del número. Bien, pues ese valor es el resto de la división de 123456789 entre 9. Como sale justamente 9, que es divisible por sí mismo, el resto en este caso es 0. Si no se lo creen, háganlo. La raíz digital de un número siempre nos da el resto de la división de ese número entre 9. La demostración matemática no es difícil, pero por no aburrir más de la cuenta, no la desarrollaremos. Existen muchos «trucos de adivinación» de magia (con números, con cartas, etc.) basados en las propiedades de la raíz digital de un número. Seguro que algunos de ustedes incluso recuerdan la célebre prueba del 9 que se enseñaba antes en las escuelas para comprobar si las multiplicaciones y divisiones estaban bien hechas (también se puede con sumas y restas). Seguro que se preguntan por qué ya no se enseña. Yo no lo sé a ciencia cierta, pero lo que sí sé es que no es una prueba infalible: si no se cumple, la cuenta está en efecto mal hecha, pero si da bien, puede que la cuenta esté mal hecha. En otra ocasión si quieren, hablamos de ello. Otro concepto imprescindible para trabajar en teoría de números son las congruencias (en este artículo de esta misma sección ya se habló de ellas mediante ejemplos). Ese concepto es precisamente el que nos facilita el resto de una división entre un número ¡¡¡sin hacer la división!!! Escribimos la definición: Un número a es congruente con otro b modulo n cuando a – b es un múltiplo de n. En lenguaje matemático,
Por ejemplo, 16 equivale a 7 (mod 9), porque 16 – 7 = 9, que es un múltiplo de 9. Esto nos dice que el resto de dividir 16 entre 9 es el mismo que el de dividir 7 entre 9 (que es 7 porque en este segundo caso, 7 < 9, y no hay tal división). Uniéndolo con lo de la raíz digital, es fácil deducir que el resto de 98765 entre 9 es 8, porque 9 + 8 + 7 + 6 + 5 = 35, y 3 + 5 = 8 (su raíz digital). Y 98765 equivale a 8 (mod 9) porque 98765 – 8 (= 98757) es un múltiplo de 9 (porque 9 + 8 + 7 + 5 + 7 = 36, y 3 + 6 = 9). Volviendo al tema de los números al cubo, resulta que sólo hay tres posibles restos al dividir el cubo de cualquier número entre 9. Veamos por qué:
Ya no hace falta continuar porque el siguiente, al ser el 9 y estar haciendo congruencias módulo 9, su resto va a coincidir con el del 3 (porque 9 = 3²), y a partir de ahí se repiten todos. En resumen, un número al cubo siempre va a tener un resto de 0, 1 u 8 al dividirlo por 9. Para ver si lo han entendido les propongo un sencillo ejercicio (tienen dos semanas para pensarlo, que descansamos con las vacaciones de Semana Santa):
Retomemos nuestra ecuación x³ + y³ + z³ = k. ¿Qué sucede al sumar tres números al cubo? Que sólo van a poder darse las combinaciones de los citados tres restos 0, 1, 8. ¿Puede la suma de tres números al cubo dar un número k que dé resto 1 al dividirlo entre 9? Sí, porque hay una suma de esos restos que da uno: 0 + 0 + 1 (también valdría 1 + 8 + 1, porque al estar con módulo 9, los múltiplos de 9 son como si fueran un 0). ¿Puede la suma de tres números al cubo dar un número k que dé resto 2 al dividirlo entre 9? Sí, porque hay una suma de esos restos que da dos: 0 + 1 + 1. ¿Y 3? También, 1 + 1 + 1. Pero 4 o 5, imposible. En cambio 6, 7, 8 o 9, sí. Para comprobar éstos, observemos que 8, es como tomar – 1 en módulo 9, porque 8 equivale a –1 (mod 9); del mismo modo 6 equivale a –3 (mod 9), 7 = –2 (mod 9) y 9 equivale a 0 (mod 9). Con esos valores, verán cómo las combinaciones de los restos 0, 1, –1 nos proporcionan esas terminaciones. Pero nunca vamos a poder tener números k cuyos restos módulo 9 sean 4 o 5. Expresado de otra forma, ningún número de la forma 9n + 4 o 9n + 5, para ningún n entero, puede ser suma de tres números al cubo. A pesar de deducir tan fácilmente este resultado, esto no nos da un procedimiento para encontrar los valores enteros de x, y, z que concretamente sumen los números k que queramos. Para algunos de ellos, muy pocos, se han podido deducir los infinitos valores que los cumplen. Por ejemplo, para la ecuación x³ + y³ + z³ = 1, se ha demostrado que los respectivos valores de (x, y, z) tienen la forma
Para cualquier valor entero de m. Pero, ¿qué sucede con otros valores de k? En principio se trató de buscar valores relativamente pequeños, pero enseguida se comprobó que este procedimiento no llevaba muy lejos. Era necesario trabajar con valores de muchas cifras. Entonces se percataron de que, en ese caso, unos valores de x, y, z deberían ser positivos, pero alguno debía ser negativo. A partir de 1950, con la aparición de los ordenadores, algunos investigadores se han centrado en idear algoritmos que, implementados en los ordenadores, nos den los valores necesarios de x, y, z para los de k concretos. Cronología sintética del problema
Aunque la resolución de ecuaciones diofánticas (se denominan así cuando sólo nos interesan las soluciones enteras) es incluso anterior a Diofanto de Alejandria (siglo III de nuestra era; fue el primero en tratar de resolver el problema de un modo sistemático, por eso se las puso su nombre, pero se han encontrado vestigios con estos planteamientos desde la época babilónica), lo cierto es que la primera referencia a esto de la suma de tres cubos aparece en The Ladies’ Diary, un almanaque editado en Gran Bretaña en el que se publicaban materiales relacionados con calendarios, con los horarios de salida y puesta del sol, las fases de la luna, así como fechas importantes (eclipses, días festivos, acontecimientos escolares, etc.) y una cronología de eventos notables. Además, incluía acertijos (los denominaba «enigmas»), jeroglíficos, charadas, preguntas científicas y preguntas matemáticas. Un volumen típico incluía las respuestas enviadas por los lectores a los problemas planteados el año anterior y una serie de problemas nuevos, casi todos propuestos por los lectores. Tanto el rompecabezas como la respuesta (revelados al año siguiente) estaban a menudo en verso. Cada portada mostraba la imagen de una destacada mujer inglesa. En el volumen 122 del año 1825 un autor llamado S. Ryley, da una solución racional general para todo valor de k (lo cual es destacable no sólo por el contexto en el que se publica, sino por su complejidad). En 1908, A.S. Werebrusov publicó una solución paramétrica general para k = 2. En 1936, el matemático alemán Kurt Mahler (posteriormente nacionalizado británico) descubre la descrita antes para k = 1. El matemático británico Louis Joel Mordell (luego nacionalizado norteamericano) demostró en 1942 que para otros valores de k, una solución paramétrica racional debería ser de grado al menos cinco. En 1954, los matemáticos británicos Jeffrey Charles Percy Miller y M. F. C. Woollett, pioneros en computación, encontraron soluciones para 69 valores de k, entre los cien primeros. Desde entonces, otros matemáticos y programadores han hallado más soluciones para valores de k, y lo que empieza a valorarse es la potencia de los algoritmos de búsqueda, siendo esenciales el de Roger Heath-Brown y el de Noam D. Elkies, aunque hay muchos más. A inicios de 2019, habiendo probado ya valores de x, y, z hasta 10 elevado a 15, no se habían encontrado soluciones aún para k < 1000, para trece valores: 33, 42, 114, 165, 390, 579, 627, 633, 732, 795, 906, 921, 975. Y por fin, la noticia El pasado 18 de marzo, el matemático británico Andrew R Booker, especialista en teoría de números y combinatoria, ha enviado un avance al portal de prepublicaciones ArXiv. En ese borrador, aporta una solución que ha encontrado para uno de esos valores desconocidos hasta ahora, k = 33: 33 = 8.866.128.975.287.528³ + (–8.778.405.442.862.239)³ + (–2.736.111.468.807.040)³ El único valor menor que 100 que queda por encontrar soluciones es k = 42. A ver si a la vuelta de las vacaciones alguno de nuestros lectores nos anuncia la grata sorpresa de haber descubierto tan ansiada solución. Alfonso J. Población Sáez es profesor de la Universidad de Valladolid y miembro de la Comisión de divulgación de la RSME. El ABCDARIO DE LAS MATEMÁTICAS es una sección que surge de la colaboración con la Comisión de Divulgación de la Real Sociedad Matemática Española (RSME) |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |