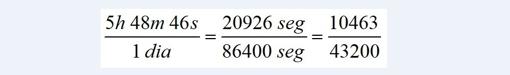Omar Khayyam, el matemático persa al que le debemos que la incógnita sea una X
Omar Khayyam, el matemático persa al que le debemos que la incógnita sea una X |
 |
 |
 |
|
ABC, 20 de Mayo de 2019 También le debemos la descripción más temprana de la potencia de un binomio con exponente natural y en establecer la idea de que las fracciones podrían constituir un conjunto numérico con propiedades más amplias que el de los números naturales, únicos conocidos entonces en su época
Representación de Omar khayyam - Adelaide Hanscom En el curso 2009 – 2010 se puso en marcha en nuestro país el Máster en formación del profesorado de educación secundaria obligatoria, bachillerato, formación profesional y enseñanza de idiomas, abreviadamente conocido como Máster de Secundaria, que sustituía al Curso de Adaptación Pedagógica (popularmente denominado CAP). Esa sustitución vino determinada por la entrada en vigor del Espacio Europeo de Educación Superior (EEES), descrito de forma sintética como Plan Bolonia. Tanto el máster como aquel curso resultan requisitos indispensables en España para que licenciados, ingenieros, arquitectos, graduados o titulaciones equivalentes puedan ejercer la enseñanza en centros de educación secundaria de acuerdo con las diferentes leyes que han ido apareciendo desde los años setenta (que han sido unas cuantas, por cierto; ya saben lo que se dice: da la impresión que cada gobierno de este país, cada nuevo ministro, desean pasar a la posteridad con la correspondiente reforma educativa y su consiguiente plan. Lo malo es que lejos de solucionar aspectos, estropean otros. Pero esa es otra historia en la que hoy no nos meteremos). Desde ese curso he impartido dos asignaturas en ese máster, en el módulo específico de matemáticas. Una de ellas, optativa, se denomina Ideas y Conceptos Matemáticos a través de la Historia, y consta de 3 créditos (30 horas de clase presenciales). Es obvio que, con ese número de horas, no es posible hacer un recorrido mínimamente digno por la Historia de las Matemáticas, de modo que los tres profesores que nos encargamos de impartirla (somos tres por aquello de que, cuando se planificó, se repartió entre diferentes especialidades), decidimos programarla de acuerdo al desarrollo histórico de, como su nombre describe, distintos hitos relevantes (ideas y conceptos), y cómo ha sido su evolución en el tiempo. En mi caso concreto, tengo a mi cargo 12 horas que reparto en cuatro temas que he considerado de interés: Ecuaciones, Geometrías no euclideas, Problemas matemáticos (aún) sin resolver y Las matemáticas en España. Pero no se equivoquen. La asignatura no consiste en una mera sucesión de datos, nombres de personas, descubrimientos y fechas. Eso aparece, pero también el desarrollo pormenorizado de diferentes técnicas que cada momento histórico tuvo. O sea, hay matemáticas explícitas, y no pocas. Considero de gran importancia que los matemáticos (científicos, en general) y más aún, los futuros profesores de matemáticas, tengan alguna idea de cómo se han desarrollado los resultados que explicamos en nuestras aulas. Muchos alumnos acaban sus estudios sin haberse parado a reflexionar cómo las matemáticas (la ciencia en general) se han fraguado. Quizá piensen que un buen día una persona muy inteligente o que no tenía nada mejor que hacer, se puso a resolver entelequias que se le iban ocurriendo, en épocas en las que no había demasiados asuntos con los que entretenerse. Cuando uno estudia historia, literatura, filosofía, etc., se topa con muchos personajes y acontecimientos que existieron, que tenían nombre y apellidos, y lo entiende. Sin embargo, con los resultados y procedimientos científicos, parece que han surgido por generación espontánea. Por supuesto, nada más lejos de la realidad. Todo tiene un proceso, a veces de siglos de diseño y perfeccionamiento. Ya lo reconoció Newton en su célebre frase: Si he visto más lejos es porque estoy sentado sobre los hombros de gigantes (y no hay duda de que Newton en persona la empleó, porque la escribió en una carta a Robert Hooke fechada el 15 de febrero de 1676; algunos estudiosos de la obra newtoniana han razonado otro tipo de interpretación más mordaz, incluso se conocen sentencias parecidas medievales, pero con el mismo sentido, el reconocimiento a los trabajos de quienes nos precedieron). En definitiva, considero (y creo que no soy el único que piensa así) que conocer mínimamente la historia de la ciencia contribuye a humanizarla (que no hace falta, porque evidentemente ¿a quién si no se le debe?). Pero más importante aún: conocer cómo se generan los problemas y cómo se dieron solución en el pasado, puede ayudarnos a resolver otros del presente, a los que nunca aplicaremos técnicas diferentes a las que nos enseñan. ¿Recuerdan uno de los momentos clave de la película «Figuras Ocultas» (2016) cuando la protagonista recurre a un procedimiento numérico para adaptar una órbita elíptica a una parabólica? Uno de sus compañeros la reprocha que use «un método obsoleto» como el de Euler para encontrar la aproximación. Pero en matemáticas no existen métodos ni resultados obsoletos. Tras este preámbulo, hoy quiero traer a escena a un matemático no demasiado conocido, pero al que se atribuyen algunos resultados bastante relevantes: Omar Khayyam (hacia 1050 – 1123). Hedonismo, poesía, amor y astronomía Seguramente las personas a los que sí le suene este nombre sea por las célebres Rubaiyat, composiciones de versos agrupados en cuartetas (su producción ronda el millar de cuartetas), que ensalzan la buena vida, el disfrute en compañía de una buena amante, un buen vino, etc., como compensación a la dureza de la vida, transmitiendo además parte de su filosofía, cargada de pesimismo, pragmatismo y escepticismo. Si además leyeron, como es mi caso, esa deliciosa novela titulada Samarcanda, del libanés Amin Maalouf, recordarán cómo una valiosísima copia manuscrita de las Rubaiyat se perdió en el hundimiento del Titanic, y cómo Omar Khayyam entra en contacto con el líder de la secta de los asesinos, oculta entre los muros de la inexpugnable fortaleza de Alamut (que es el título de otra destacable novela de Vladimir Bartol, e inspiradora de la saga de videojuegos serie de videojuegos Assassin's Creed). Pero nuestro personaje es tanto o más relevante por sus trabajos en matemáticas y sobre todo, astronomía. Hacia 1092, a su regreso de la obligada peregrinación a la Meca de los musulmanes, desempeña trabajos en múltiples disciplinas entre las que destacan la historia, la enseñanza de las matemáticas, la astronomía, la medicina o la filosofía. Escribió muchos tratados de carácter científico (varios hoy perdidos) y fue capaz de determinar con mucha precisión el error del calendario persa de 365 días. La propuesta de calendario de Khayyam yerra un día en 3770 años, menos que el del calendario gregoriano (un día en 3330 años), que se empezó a usar en Europa a finales del siglo XVI (recordemos que Khayyam es del siglo XI). De hecho, sigue siendo el calendario vigente aún hoy en Irán y Afganistán. Aunque el tema del calendario merece por sí mismo una entrada propia, describiré a grandes rasgos la proeza de Khayyam para que se hagan una idea. Nuestro calendario se basa en el concepto de año trópico (o año tropical) porque es el que regula las estaciones. Un año trópico es el tiempo que transcurre entre dos pasos consecutivos del Sol por el equinoccio de primavera (el primer día de la primavera). Se elige ese día porque es uno de los momentos del año en los que el Sol está situado exactamente en el plano del ecuador celeste. Ese día, para un observador situado en el ecuador terrestre, el Sol alcanza el cenit, es decir, el punto más alto en el cielo. En ese momento la declinación del Sol y el ecuador celeste coinciden. Pues bien, ese valor es exactamente 365 días 5 horas 48 minutos 45.10 segundos, que pasado a cifra decimal es 365.242189 días. Esa parte decimal, 0.242189, es la causa de que debamos añadir un día cada cuatro años para ajustarnos al recorrido del Sol. Si transformamos esa parte decimal en forma racional, es decir en una fracción, obtenemos:
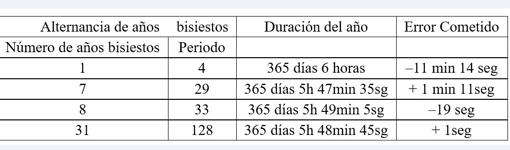
Si utilizamos una fracción continua, el año se expresa así: 1 año = 365 días 5 horas 48 minutos 46 segundos = [365; 4, 7, 1, 3, 5, 64] Mediante la aplicación de ecuaciones diofánticas a esa fracción continua, podemos conformar una tabla con las siguientes aproximaciones (no sé si todos los lectores estarán familiarizados con las fracciones continuas y las ecuaciones diofánticas; para lo que pretendo hoy mostrar no hace falta saber nada de ellas, pero en próximas reseñas explicaré su fundamento con más detalle porque tiene aplicaciones curiosas en nuestra vida cotidiana):
Si nos fijamos en las dos últimas filas de la tabla, cada columna muestra una aproximación racional cada vez mayor a la fracción final 10463/43200 que es el desfase decimal que se produce cada año, es decir, ese 0.242189. Tomar los valores de la segunda columna, es decir, ¼, es aproximar el valor por 0.25, que corresponde a la corrección del Año Juliano (la corrección ideada por Julio César: añadir un año bisiesto cada cuatro años). La tercera columna es más precisa, ya que tomar la fracción 7/29 es tomar 0.241379. La cuarta columna es la corrección propuesta por Omar Khayyam, es decir, 8/33, que es aproximadamente 0.2424242424. Os muestro una tabla con los desfases de cada sistema, para que os hagáis una idea:
Desafortunadamente, Omar Khayyam no pudo concluir las tablas astronómicas que empezó a confeccionar completamente a causa de las muertes de sus principales valedores (Malik Shah, fundamentalmente, nieto del fundador de la dinastía selyúcida) junto al desmantelamiento del observatorio astronómico de Isfahán, que dirigió durante dieciocho años. En reconocimiento a su trabajo en relación a la Astronomía, en 1970 se bautizó un cráter en la Luna con su nombre (ya saben que a la mayor parte de los accidentes geográficos lunares se les ha dado el nombre de algún científico), y al asteroide 3095 descubierto en 1980 también se le denominó Omar Khayyam. Pionero en matemáticas Para presentar el tema Ecuaciones en la asignatura del máster que comenté al inicio, primero muestro a los alumnos algunas escenas de películas en las que aparecen directa o implícitamente menciones a ecuaciones de segundo y tercer grado. Una de ellas corresponde a «El pequeño Tate» (1991) sobre un niño prodigio de las matemáticas en una familia monoparental de pocos recursos. Descubierto por una profesora, lo inscribe en un concurso (que existe en la realidad) norteamericano conocido como Odisea de la Mente. Una de las cuestiones que debe resolver mentalmente es «¿Qué número tiene la siguiente peculiaridad: si añadimos su cubo a cinco veces su cuadrado y del resultado restamos 42 veces el número y luego 40, el resto es cero?». Su respuesta es prácticamente inmediata, 5. Con la excusa de resolver la ecuación cúbica resultante
Realizo un recorrido por el modo que diferentes matemáticos han dado a lo largo de la Historia: Omar Khayyam (siglos XI – XII), Leonardo de Pisa, “Fibonacci” (s. XIII), “Tartaglia” y Cardano (s. XVI), François Viète (s. XVI), Transformaciones de Tschirnhaus (s. XVII), Resolventes de Lagrange (s. XVIII) y Radicales de Chebyshev (s. XIX). También realizamos un repaso por diferentes métodos de localización de las raíces, como los polinomios de Sturm y la regla de los siglos de Descartes, y los métodos numéricos de Bisección, Regula Falsi, Secante, Newton y otros métodos de punto fijo. Las tres horas que utilizamos nos quedan bastante justas ciertamente. Aunque se cree que los egipcios ya debieron toparse con ecuaciones cúbicas en su intento de duplicar el cubo con regla y compás, no se han encontrado evidencias de ello hasta los griegos hacia el siglo V a. C. Khayyam piensa que las ecuaciones de grado mayor o igual al tercero no pueden resolverse con regla y compás (lo cual fue demostrado 750 años después), por lo que su tratamiento a la hora de resolver cúbicas es geométrico. De acuerdo a Carl B. Boyer en su Historia de las Matemáticas, retoma las ideas de Menecmo, Arquímedes y Alhazen en busca de las posibles raíces reales de las cúbicas, mediante la intersección de diferentes secciones cónicas, que manejaba con soltura. Elige una parábola del tipo x2 = 2py, siendo p cualquier valor racional, y la sustituye en la ecuación cúbica que quiere resolver. Si tomamos por ejemplo la parábola:
Y la sustituimos en la cúbica:
Obtenemos la hipérbola:
(Supongo que el lector obtendrá esa ecuación con facilidad: no tiene más que poner x^3 como x^2 por x, y sustituir el valor de x^2 por 20y)
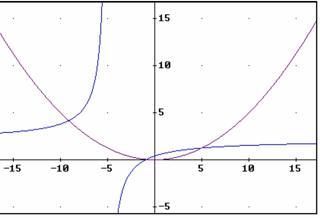
En la imagen adjunta se han representado las dos cónicas (la de color morado es la parábola, y la azul la hipérbola). Las abscisas de los puntos de corte de ambas, son las soluciones de la cúbica original. Como hay tres, la cúbica tiene sus tres raíces reales. Obsérvese que, mediante este procedimiento, Khayyam reduce la ecuación de tercer grado a un sistema de dos ecuaciones, ambas de segundo grado. Es decir, reduce un grado a costa de introducir una ecuación nueva, pero las dos que le resultan las maneja con soltura al ser cónicas con las que está familiarizado. Si resolvemos algebraicamente ese sistema de dos ecuaciones, se obtienen sin dificultad las tres raíces reales:
A Omar Khayyam también le debemos la descripción más temprana de la potencia de un binomio con exponente natural y en establecer la idea de que las fracciones podrían constituir un conjunto numérico con propiedades más amplias que el de los números naturales, únicos conocidos entonces. Estas ideas teóricas se contaron entre las matemáticas punteras durante el Renacimiento europeo. En 1070 escribió Tratado sobre demostraciones de problemas de álgebra, que contiene una completa clasificación de ecuaciones cúbicas resueltas geométricamente, mediante la intersección de secciones cónicas, como hemos tratado de mostrar en el ejemplo anterior. También parece confirmado que a Khayyam le debemos el que la incógnita de las ecuaciones se llame x. Él la llamó shay (que significa “cosa", en árabe), que se europeizó como xay, (la x tenía el sonido sh), y de ahí derivó a la inicial x. Existen al menos dos películas en las que aparece nuestro personaje, ninguna estrenada en España en salas comerciales: Omar Khayyam (The Live, Love and Adventures of Omar Khayyam, William Dieterle, EE. UU., 1957) que puede adquirirse en DVD y que no es más que una película de aventuras al estilo de Las mil y una noches, y la más reciente y mucho más interesante «The Keeper: The Legend of Omar Khayyam» (2005). En este enlace puede verse una completa descripción de la misma y de las matemáticas que contiene . Alfonso J. Población Sáez es profesor de la Universidad de Valladolid y miembro de la Comisión de divulgación de la RSME. El ABCDARIO DE LAS MATEMÁTICAS es una sección que surge de la colaboración con la Comisión de Divulgación de la Real Sociedad Matemática Española (RSME) |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |