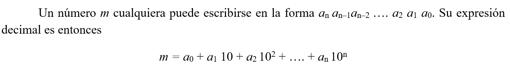La «regla del siete» que sí funciona y no te explicaron en la escuela
La «regla del siete» que sí funciona y no te explicaron en la escuela |
 |
 |
 |
|
ABC, 7 de Octubre de 2019 Dos criterios de divisibilidad que probablemente no conocías y no son magia
Adobe Stock
Cuando estudiamos en la escuela las reglas de divisibilidad, aprendemos unos criterios para averiguar de un modo sencillo (sin dividir por el número en cuestión) si un número es divisible por 2, 3, 5, 6, 8, 9 y 10, esto es, si el resto es cero. En planes de estudio más antiguos, también se enseñaba cuando un número era divisible por 11, e incluso por 13. Pero en prácticamente ningún caso, se nos enseñaba una regla para la división entre 7. Los alumnos encantados, cuanta menos materia se nos diera, mejor. Pero, quien más, quien menos se preguntaba, aunque no lo manifestara, ¿por qué? ¿Será que el criterio es muy complicado? O a lo mejor ni existe tal criterio. Hoy trataremos de arrojar alguna luz (confío) sobre el asunto. De paso, satisfacemos a un lector que en una ocasión nos sugirió en un comentario a una entrada anterior que para cuando la regla del 7 (bien es cierto que lo expresó de modo sarcástico ante lo que consideraba una reseña demasiado elemental, pero es una buena excusa para repasar y quizá aprender algo nuevo). Para empezar, digamos que los criterios de divisibilidad no son únicos. Hemos aprendido los más simples, sencillos y prácticos, pero hay muchos. En el caso del 7, echemos un vistazo a un par de ellos, y cada cual que se quede con el que más le guste, o considere más sencillo de recordar y aplicar. Primer intentoCojamos los dígitos del número en orden inverso, es decir, empezando desde las unidades, multiplicándolos sucesivamente por 1, 3, 2, 6, 4, 5, repitiendo esta sucesión de multiplicadores si es necesario. Después sumamos todos esos productos. Esta suma tiene el mismo resto que el número inicial si lo dividimos por 7 (matemáticamente esto se expresa como que ambos son congruentes módulo 7). Comprobémoslo mediante un ejemplo. Ejemplos: ¿Es 2359 divisible por 7? 9 x 1 + 5 x 3 + 3 x 2 + 2 x 6 = 42 Como 42 es divisible por 7, también lo es 2359. Observamos que este método se basa en encontrar un número más bajo que tenga las mismas características ante el 7 que el que buscamos, y es el que nos “aclara” lo que sucede. El inconveniente de este procedimiento es que, si el número original es muy alto, puede resultar más sencillo dividir directamente por 7 (con lo cual, el método no sería práctico). Por ejemplo, queremos saber si 9999999 es divisible por 7. Deberíamos efectuar entonces esta operación: 9 x 1 + 9 x 3 + 9 x 2 + 9 x 6 + 9 x 4 + 9 x 5 + 9 x 1= 198 ¿Y ahora qué hacemos con 198? ¿Lo dividimos por 7? Para eso, habíamos dividido el primero y ya habríamos terminado. Aunque siempre podemos volver a repetir el algoritmo: 8 x 1 + 9 x 3 + 1 x 2 = 37 Concluimos por tanto que el original no es divisible por 7. Pero, ¿por qué funciona el procedimiento? O, dicho de otro modo: hagamos una demostración, porque parece un poco “raro” tomar precisamente esos valores (1, 3, 2, 6, 4, 5). ¿De dónde salen? Mucha gente piensa a veces que las matemáticas son como algo mágico, en donde las cosas funcionan, pero no se sabe muy bien porqué, y nada más lejos de la realidad (a diferencia de tantas patrañas como nos cuentan diariamente por ahí). Si nos perdemos alguna cosa es, sencillamente, porque o no nos dicen la prueba, o no nos molestamos en pensarla. Para poder hacer la demostración necesitamos algunas herramientas (como en cualquier otro oficio; aquí no son destornilladores, ni martillos, sino definiciones, propiedades, teoremas). Recordemos que alguna vez ya hemos hablado de las congruencias , concepto esencial para demostrar muchas propiedades de los números ahorrándonos tediosas operaciones. Brevemente, un número a es congruente con otro b modulo n cuando a – b es un múltiplo de n (es decir, a – b es divisible por n). En lenguaje matemático,
Las congruencias verifican algunas propiedades respecto a la suma y al producto (las describo porque necesito utilizarlas, no para llenar espacio). Por ejemplo, si en una congruencia sumamos la misma cantidad en ambos miembros, el resultado mantiene la congruencia (es decir, da el mismo resto, en la división). También si multiplicamos los miembros por el mismo número entero. De nuevo, en lenguaje matemático, es visualmente más fácil de recordar:
La demostración de estas propiedades es muy sencilla (los matemáticos decimos “inmediata”, y en ese caso, ni nos molestamos en detallarla, porque basta con ponernos a escribirla para dar con ella; pero aquí la vamos a relata, para que vean que, en efecto, es sencilla). Fíjense que para probar la congruencia i) hay que ver (de acuerdo con la definición previa) que existe un número entero k tal que (b + s) – (a + s) = k n Efectuando la resta nos queda b – a = k n, y esa condición es de la que partimos como cierta (a es congruente con b (mod n)), por lo tanto la afirmación está probada. Del mismo modo, para ii), habría que demostrar que bs – as es un múltiplo de n, y como b – a = k n, y bs – as = s (b – a), entonces bs – as = sk n, y habríamos encontrado un múltiplo entero de n (el entero sk). Volvamos al primer método de divisibilidad por 7. Las potencias de 10 tienen los siguientes restos al ser divididos por 7:
Obsérvense que los restos que salen son (¡¡oh, magia!!) justamente los números por los que multiplicábamos los dígitos del número que queríamos ver si era o no divisible por 7. A partir del séptimo (la potencia 10 6 ; ¡¡más magia!!), se empiezan a repetir.
Utilizando la propiedad ii) citada anteriormente (la de que, al multiplicar una congruencia por un número entero, la congruencia, o sea el resto de la división, se mantiene), el cuadro de arriba se convierte en
Y finalmente, una última propiedad de las congruencias:
Así que
Es decir, m en expresión decimal tiene el mismo resto al ser dividido por 7 que
En particular, si el segundo tiene resto cero (es divisible por 7), el primero también. Por eso funciona el procedimiento. Pero ya hemos visto que tiene un inconveniente: a veces hay que hacer más operaciones con el método que dividiendo directamente entre 7 (lo que coloquialmente decimos “matar moscas a cañonazos”). Así que vamos a ver si encontramos una herramienta mejor. Segundo métodoA partir del número del que deseamos saber si es divisible por 7, multiplicamos por dos su cifra de las unidades, y restamos la cantidad resultante del número que queda al eliminar del original la mencionada cifra de las unidades. Repetimos este proceso con el número obtenido hasta que nos quede un solo dígito. Si éste es 0 o 7, entonces el número original es divisible por 7. Ejemplo: Volvamos a probar con el 2359. La cifra de las unidades es un 9, que doblamos, resultándonos 18. Entonces restamos 235 – 18 = 217. Repetimos el algoritmo con éste número, esto es, 21 – 14 = 7. Como el resultado ha sido 7, el número inicial es divisible por 7. Para el segundo número, 9999999, procederíamos así:
Pues bien, el primer miembro, 10 A + B, es cualquier número de dos cifras (B son las unidades, y A las decenas). En el segundo miembro, A – 2B es coger las decenas y restarle el doble de las unidades (lo que haría el método si el número fuera sólo de dos cifras). Y ambas expresiones se comportan igual al ser divididas por 7. Si funciona para números de dos cifras, es sencillo generalizarlo a números de más dígitos (seguro que el lector es capaz de terminar la prueba por si solo). El 7 aparece en muchos “trucos”, juegos, ejercicios y cuestiones numéricas, en nuestra cultura, en la vida cotidiana (ojo, como cualquier otro número; no se crean nada de las tonterías numerológicas de que es un número sagrado, mágico y demás paparruchas. Cada número tiene sus particularidades y punto). Por ejemplo, seguro que conocen el famoso “truco” de adivinación que tiene como base el número 142857, el número cíclico más pequeño (se llama así porque ese número multiplicado por cualquier digito del 1 al 6, nos da como resultado un número en el que aparecen los mismos dígitos en otro orden). Pues bien, calculen 1/7 a ver qué les sale (miren los seis primeros decimales, y luego los seis siguientes, y los seis siguientes, etc.). Y como fin de fiesta les propongo una cuestión con la que alguno seguirá pensando que el 7 es, cuanto menos, extraordinario (conste que ésta me la he inventado yo). Tenemos un montón de sillas apiladas unas sobre otras, y tenemos que colocarlas para ver una actuación. Queremos colocarlas de modo que formen un rectángulo perfecto, es decir, que no quede ninguna fila o columna más larga que otra. No tenemos tiempo para contarlas, son muchas, y el show comienza en breve, así que hay que ponerse manos a la obra. ¡Qué mala suerte! No damos con la configuración adecuada. Hemos intentado colocarlas en 2, 3, 4, 5, 6, 8, 9 y 10 filas. ¡¡Y siempre sobra una!! Hasta que llego yo (para eso me lo invento, ¿no?), y pregunto “inocentemente”: ¿Y por qué os habéis saltado el 7? La respuesta que recibo es la habitual en los anuméricos: ¿Estás tonto? El 7 es impar, primo y no cuadra con nada. ¡¡No tenemos tiempo que perder!! Lo que vamos a hacer es quitar una silla y ya está. Mi respuesta es obvia: Anuméricos y tramposos. El reflejo evidente de lo que nos rodea. Probad con el 7, haced el favor. El amable y aplicado lector deducirá cómo acaba la historia. En efecto, un rectángulo perfecto gracias al “mágico” 7. Ahora os toca a vosotros decirnos cuántas sillas había en total, sabiendo que no llegaban al millar, pero pasaban de las quinientas. Que ustedes lo disfruten . Alfonso J. Población Sáez es profesor de la Universidad de Valladolid y miembro de la Comisión de divulgación de la RSME. El ABCDARIO DE LAS MATEMÁTICAS es una sección que surge de la colaboración con la Comisión de Divulgación de la Real Sociedad Matemática Española (RSME) |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |