Para qué sirven los logaritmos: dos retos sin usar la calculadora
Para qué sirven los logaritmos: dos retos sin usar la calculadora |
 |
 |
 |
|
ABC, 25 de Noviembre de 2019 Aparecen en muchas de las cosas que tenemos a nuestro alrededor y utilizamos habitualmente, desde las canciones a los contactos en una red social
Adobe Stock
Antes de nada, me gustaría expresar mi agradecimiento a todos los lectores que se acercan semanalmente a esta sección tratando de buscar alguna explicación, alguna noción o aplicación, por simple curiosidad o el motivo que sea, a las matemáticas. Y sobre todo a aquellos que enriquecen, opinan, critican y sugieren en el apartado de comentarios. Por supuesto por su maravillosa educación y respeto al hacer dichos comentarios. Me gustaría responderlos todos y expresarles este agradecimiento, pero me es difícil (me llevaría mucho tiempo). En cualquier caso, no duden que los leo todos, al menos un par de veces, en distintos días y momentos (por aquello de que no influya mi estado de ánimo en su interpretación). En este tema de los logaritmos, he detectado dos grupos claramente diferenciados: los que lo conocen y dominan (a los que volveré a mencionar al final) y los que manifiestan su sentimiento de no acabar de entender algunas cosas (que consideran excesivamente técnicas; en ellos incluyo los que dicen no comprender nada). Estas reseñas tratan de ser entendibles por todo el mundo (no siempre se consigue; disculpas), sin que reproduzcan lo que aparece en los libros de texto (que están en general bien escritos, pero esto no trata de retornar a una clase tradicional), alternando a veces con reflexiones cotidianas (para que sean más llevaderas) y describiendo aplicaciones, en la medida de lo posible, que nos convenzan de la necesidad y potencia de las matemáticas. Los que trabajamos con las matemáticas de uno u otro modo, nos quejamos con frecuencia de la deficiente cultura matemática de la sociedad. Eso incluye entender y no espantarse por fórmulas, símbolos, ni expresiones numéricas. Es más complicado manejar un móvil o un mando a distancia (que también se fundamentan en itinerarios lógico-matemáticos, por cierto). Sólo debería requerir un pequeño esfuerzo. Si aun así no entendemos la mayor parte (todo no porque, en efecto, alguna cosilla se intenta que sea de mayor nivel, para abarcar también a personas con más nivel), es que nuestra base matemática es baja.
También queremos transmitir que no debemos establecer una competición en “nivel de importancia” con las humanidades. Ninguna disciplina es más importante que las demás (y eso incluye aquellas que muchas veces consideramos “menores”, y no lo son, como la música, la educación física, etc.). Todas son necesarias y útiles. Y se complementan perfectamente, porque forman parte de la vida total de una persona. De modo que, por favor, olviden expresiones como “yo soy de letras”, “la belleza está en la poesía”, y frases similares tan desafortunadas como huecas y falsas. De hecho, seguramente la disciplina más cercana a las matemáticas sea la filosofía (y podemos demostrarlo sin demasiada dificultad). Una de mis aficiones preferidas es el cine (aprovecho para recomendarles la sección Cine y Matemáticas que escribo desde hace dieciocho años en DivulgaMAT). Pues bien, en muchas más ocasiones me han llamado friki en conversaciones cotidianas por hablar de cine que por hablar de matemáticas. Y la frecuencia con que trato ambas es similar. Finalmente, indicar que la reseña de los logaritmos era una pequeña introducción histórica de por qué surgieron. En efecto, son mucho más interesantes hoy en día sus aplicaciones que la multiplicación o división de números grandes. Pero quería que hiciéramos un viaje al siglo XVI y nos encarnáramos en personas de aquella época, para valorar sus pensamientos y trabajos. Con ello seguimos hoy…. Los retos propuestosComenzaremos resolviendo las cuestiones planteadas en el artículo anterior. Seguramente recordaremos en nuestros años escolares al profesor proponiendo ejercicios que posteriormente nunca corregía. Esa práctica (habitual cuando se va con el tiempo justo para terminar un temario o cuando el docente no percibe demasiado interés por parte de los alumnos hacia la asignatura) personalmente me enervaba bastante, sobre todo si había intentado resolver las cuestiones. ¡¡No sabías si lo habías hecho o planteado bien!! No digamos si no tenías ni idea de cómo resolverlo (y seamos sinceros: nunca se iba a preguntar al profesor a la sala de profesores o se pedía una tutoría, al menos en los años que yo cursé la enseñanza secundaria). De modo que no voy a hacer lo mismo, y voy a resolver lo que les planteé en los retos propuestos. Reto 1: En primer lugar, habíamos tratado de encontrar mediante logaritmos (es decir, haciendo sumas en lugar de multiplicaciones) el producto de 2828 por 5257. Para ello teníamos como única ayuda una sola hoja de las tablas de logaritmos decimales (en base diez) con valores entre 10 y 54 y cuatro cifras significativas. Obteníamos como solución solamente las cuatro primeras cifras del resultado, 1486, y les planteaba si, con la única ayuda de esa hoja y sus conocimientos matemáticos, se podría encontrar la solución exacta y completa, que es 14866796. En sus respuestas no he visto ninguna que haya abordado estas cuestiones, de modo que les indico la que he pensado yo, pero por supuesto, habrá otras, seguramente mejores. Estarán de acuerdo en que podemos expresar 2828 como 2800 + 28, y 5257 como 5200 + 57. Entonces, 2828 • 5257 = (2800 + 28) • (5200 + 57) = (2800 • 5200) + (5200 • 28) + (2800 • 57) + (28 • 57) Evidentemente no podemos romper la norma que nos hemos impuesto de no hacer multiplicaciones (por comodidad, vagancia, por ser tedioso, o porque no sabemos, por la razón que sea), pero si usaremos algo para lo que no hace falta esfuerzo alguno: que para multiplicar algo por una potencia de 10, basta con añadir tantos ceros como indique el exponente de esa potencia. Si nos fijamos en los cuatro paréntesis que nos han salido, tenemos que encontrar el valor de dos productos: 28 • 52 y 28 • 57. Para ello, tenemos que apañarnos SOLO con la hoja del artículo anterior. La primera multiplicación es sencilla utilizando el procedimiento descrito el otro día: log10(28) + log10(52) = 1,4472 + 1,7160 = 3,1632 Al aparecer en la parte entera un 3, sabemos que el número correspondiente tiene que estar entre 1000 y 9999. Recordemos la razón: log10(103) = 3 log10(10) = 3 A continuación, buscamos en la tabla el valor 1632. El más cercano, sin sobrepasarlo, es 1614, que corresponde a la fila del número 14, columna 5. De modo que nuestro número empieza por 145. Para encontrar la cifra de las unidades, calculamos la diferencia entre el valor que buscamos, 1632, y el que aparece en la tabla, 1614, que es 1632 – 1614 = 18. En la tabla, en el apartado Partes Proporcionales, localizamos el número más próximo a 18. Resulta que 18 está exactamente en la columna del 6. Por tanto, el número que buscamos es 1456. Y en efecto, 28 • 52, es exactamente ese valor. El primer paréntesis que teníamos era 2800 • 5200, que es lo mismo que 28 • 10^2 • 52 • 10^2, es decir, 28 • 52 • 10^4 (recuerden que para multiplicar potencias de la misma base se suman los exponentes), es decir, 1456 • 10^4, que es 14560000. En el segundo paréntesis tenemos 5200 • 28, que es 28 • 52 • 10^2, y por tanto el resultado es 145600. Para los dos paréntesis siguientes necesitamos conocer el producto de 28 • 57. Obviamente tenemos que hacer lo mismo que antes, calcular con ayuda de la tabla log10(28) + log10(57) Y encontramos un problema: lamentablemente 57 no está en nuestra hoja. Pero, ¡¡sabemos las propiedades de los logaritmos!! (que pusimos también en el artículo anterior). Probemos a poner el 57 como producto, cociente o potencia de otros números que sí aparezcan en la tabla. El primero que se me ocurre: 57 = 28.5 • 2. Entonces, por la propiedad del producto log10(57) = log10(28,5 • 2) = log10(28,5) + log10(2) Nuevo contratiempo. Con la hoja podemos hallar el logaritmo de 28.5, pero, ¿qué hacemos con el 2? Seguramente hayan oído aquello de quien hace un cesto, hace ciento, así que simplemente tenemos que expresar el número 2 como producto, cociente o potencia de valores que se encuentren en nuestra hoja, es decir, entre 10 y 54. A mí se me ocurre así:
Por tanto, log10(2) = log10(50/25) = log10(50) - log10(25) Recapitulando, log10(28) + log10(57) = log10(28) + log10(28,5) + log10(50) - log10(25) En la hoja de marras, encontramos entonces que log10(28) + log10(57) = 1,4472 + 1,4548 + 1,6990 - 1,3979 = 3,2031 Y al buscar el valor 2031, llegamos al número de cuatro cifras 1596 (que es exactamente el valor de 28 • 57). Entonces, el tercer y cuarto paréntesis resultan ser 159600 y 1596. Por tanto, 2828 • 5257 = 14560000 + 145600 + 159600 + 1596 = 14866796 Recordemos que estamos realizando operaciones matemáticas como las hacían en los siglos XVI, XVII, XVIII, XIX, y parte del XX. Tenían dos opciones: o multiplicar números enormes (de 25 cifras por 40 cifras, no este ejemplillo que hemos utilizado) o utilizar las tablas de logaritmos. Estarán conmigo que mejor la segunda opción; aunque parezca larga, con práctica, es mucho más rápida y segura (sin cometer errores) que la primera. Y por supuesto, ¡¡¡benditas calculadoras y ordenadores!!! Sería absurdo negar la evidencia. Reto 2: ¿Hay alguna operación que no podamos hacer SOLO con la hoja que hemos venido empleando? Porque da la impresión de que podríamos hacer cualquiera. Y si fuera así, ¿para qué se necesitaba el famoso libro de tablas que generaciones anteriores tenían que comprar complementariamente al libro de texto? Sinceramente. no me he puesto a pensar una multiplicación o división concreta que no pueda hacerse con esa hoja. Supongo que algo del tipo 9769 • 8645, es decir, valores claramente fuera del intervalo entre 10 y 54. Pero da igual. Mi intención era mostrar que, con conocimientos no muy extensos, se puede sacar mucho partido a una simple hoja. Seguramente por ello se dejó de exigir comprar esas tablas, y los libros de texto añadieron en las hojas finales, media docena de tablas (las logarítmicas y las trigonométricas) con las que hacer cualquier cálculo que fuera necesario (por supuesto con fines exclusivamente didácticos, como he pretendido hacer aquí; en mi época de BUP ya había calculadoras, aunque desgraciadamente, estaban prohibidas en clase y en los exámenes. ¡¡Gran error!! Lo que hay que hacer es ENSEÑAR A USARLAS BIEN, no prohibirlas, y debo decir, bien alto que, A DIA DE HOY SIGUEN SIN HACERLO. ¡¡Aburrimos a nuestros alumnos!! La tecnología está para ser usada, señores. No quiero salirme del asunto, y por supuesto, veo que cada día los alumnos operan peor, no tienen soltura con las operaciones, DEBEN ejercitarse, pero eso no significa que no aprendan a manejarse con las herramientas adecuadas, que para eso están. Lo que les he contado está muy bien como repaso histórico, para comprender que la ciencia no se ha sabido desde siempre, para VALORAR lo que tenemos hoy, pero nada más. El alumno de hoy debe resolver y entender otro tipo de situaciones, porque las matemáticas permiten hacerlo, y no las estamos sacando ni la décima parte del potencial que tienen). La respuesta a por qué tantas tablas, es evidente: por comodidad, para no tener que dar las vueltas que hemos dado hoy con este ejemplo. Igual que hoy compramos un ordenador o un móvil mucho más potente que el que necesitamos (aunque más de uno sea para jugar a marcianitos con gráficos mejores; porque no se engañen: nos venden el mismo juego mil veces y lo pagamos como tontos. El juego es el mismo de toda la vida, lo único que cambia son los gráficos, el sonido y cuatro tonterías. Pero nos encanta la superficialidad de estar a la última. Me alegro, esencialmente, por mis alumnos del grado de informática. Tienen el futuro asegurado sólo con retocar un poco el programa básico de siempre). Bases distintasVolviendo a los logaritmos, cualquiera que esté siguiendo esta columna pensará en este punto que, si todo se puede hacer con los logaritmos en base diez (logaritmos decimales), ¿para qué en base 2, base 3, los neperianos (base el número e)? La respuesta es que cada base es conveniente para según qué problema abordemos. Por ejemplo, la base 10 es útil para saber el orden de magnitud de una cantidad, sin tener que conocerla exactamente. En el ejercicio que hemos hecho hemos visto que log10(1596) = 3,021
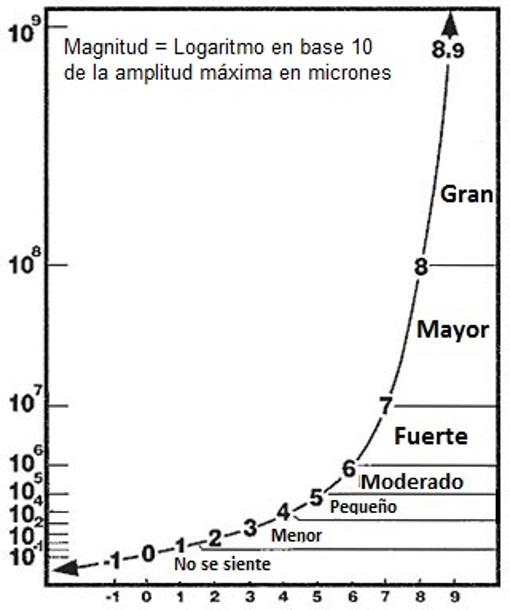
Si la parte entera de un logaritmo decimal es 3, ese número es de cuatro cifras (una unidad más que esa parte entera). Pensemos en la escala Ritcher que mide la intensidad de un seísmo (creada en 1935 por el sismólogo estadounidense Charles Francis Richter, es el baremo más preciso de que disponemos para cuantificar la magnitud de un seísmo). Un terremoto de magnitud 3 vendría a decirnos que es diez veces más fuerte que uno de magnitud 2. Está diseñada a escala logarítmica decimal, como vemos en la imagen. Confío en que al menos una cosa les quede clara: siempre que estemos manejando un asunto en el que los valores son muy grandes, se utiliza la escala logarítmica. Imaginen los datos de población de un año en una ciudad de más de un millón de habitantes. No podemos hacer una gráfica que nos dé una idea de la evolución de la población con la misma escala en el OX que en el eje OY, sencillamente ¡¡¡porque no nos cabe!!! El rango de variación es demasiado grande. Entonces, como en el gráfico anterior de la escala Richter, el eje OX toma valores en unidades, mientras que el OY lo toma en potencias de 10. Alguno estará pensando que, en esa imagen, la gráfica es la de una función exponencial, no la de una logarítmica. Y tiene razón. Pero muchas veces, para que se comprenda mejor un concepto, se cambia lo que aparece en el eje de las X (el horizontal) con el de las Y (el vertical). Es lo que pasa en la gráfica anterior, para que se aprecie mejor la apreciación de “Moderado”, “Fuerte”, etc. Si describiéramos la gráfica como debe ser desde el punto de vista matemático, deberíamos colocar esos nombres en vertical, y se lee mucho peor. Por eso se opta por intercambiar los ejes, por claridad. Lo que tenemos que tener claro es que un fenómeno exponencial y uno logarítmico expresan des caras de la misma moneda, como quedó claro el otro día, espero, cuando dibujamos ambas, para mostrar que una función es inversa de la otra.
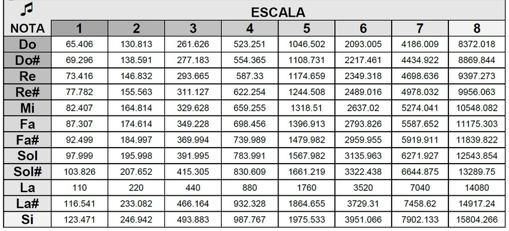
Otra base muy frecuente es la base 2. Con ella se da la idea de cuántas veces se duplica algo. Por ejemplo, en la escala musical. Observen en la siguiente tabla las frecuencias en hertzios de las notas musicales entre distintas octavas (estos valores se utilizan, por ejemplo, para afinar instrumentos musicales). ¿No notan nada extraño en esos valores? Cojan cualquiera de ellos, los de la nota La, por ejemplo, por aquello de que todos los valores son enteros, sin decimales. Al cambiar de octava, los valores van multiplicados por potencias de 2 (2, 2^2, 2^3, 2^4, …). Con los logaritmos en base 2 se puede, por ejemplo, contar cuántas octavas separan un par de notas. La base e, la de los logaritmos neperianos, la utilizamos los matemáticos en estudios teóricos porque ese número irracional, el e, aparece constantemente a nuestro alrededor (aunque no es el mejor ejemplo, porque es de creación humana, el cálculo del interés compuesto determina nuestras ganancias, perdidas, anualidades, hipotecas, etc. utiliza el número e y los logaritmos neperianos, por tanto). AplicacionesLos lectores han dado muchas aplicaciones en los comentarios de la reseña anterior. Cada una de ellas merecería una explicación detallada que ahora, visto el tamaño que ha alcanzado ésta, no debo desarrollar. Simplemente enumero algunas, y con ello, a ver si convenzo a aquella persona afirmaba que en su vida diaria nunca ha necesitado de los logaritmos, excepción hecha de tener que aprobar un examen de matemáticas del curso correspondiente. Aparecen en muchas de las cosas que tiene a su alrededor y que usa habitualmente (seguro que alguna vez ha escuchado alguna canción; ya he puesto el ejemplo de las escalas musicales), pero no lo sabe. Hablemos, por ejemplo, de la ley de Fechner, en psicología, que establece que la intensidad de nuestras percepciones varía según el logaritmo natural (el neperiano) de la intensidad de un estímulo. Hablamos de determinar el crecimiento o decrecimiento de una planta, la evolución de una sustancia radiactiva o de un virus (biológico o informático), de cómo se disuelve una determinada sustancia en una disolución, hablamos de las conexiones entre los contactos de una red social, hablamos de determinar la acidez de una sustancia (cálculo del pH), hablamos de acústica en la determinación de los decibelios (nivel de intensidad) de los sonidos. Podemos llenar varias páginas, pero resumiendo tal y como lo ha expresado un lector en su comentario, que lo ha hecho magistralmente: en cualquier fenómeno de tipo exponencial para el que queramos encontrar relaciones entre su comportamiento y sus causas, en los que pequeños cambios provocan grandes variaciones (pero determinados y conocidos, a diferencia de los que estudia la teoría del caos), el manejo de los logaritmos es, nos guste o no, IMPRESCINDIBLE. A modo de cierreEn el año 1914, historiadores de la Ciencia, matemáticos, profesores, conmemoraron por todo lo alto la aparición de las primeras tablas de logaritmos en 1614, la creación del barón escocés, matemático aficionado y fanático religioso John Napier. Le llevó 20 largos años confeccionarlas. El mundo estaba agradecido por tan útil regalo. Cien años después, en 2014, todos llevamos en el bolsillo mucho más que unas tablas, que ya no son necesarias, ni nadie enseña cómo se utilizan, porque es bastante tedioso, como hemos visto. Nadie recordó que durante tres siglos eran imprescindibles, pero, sobre todo, nadie se acordó de la genial idea de poder calcular multiplicaciones mediante sumas y divisiones mediante restas. Y lamentamos tener que leer algo que no vamos a emplear nunca más de ese modo. Pero me ha parecido que es instructivo recordar alguna vez que hubo un tiempo en el que el hombre no disponía de casi nada, y se tuvo que apañar, con un ingenio que, a lo mejor por culpa de la comodidad de las máquinas, hoy brilla por su ausencia (en todos los órdenes). Alfonso J. Población Sáez es profesor de la Universidad de Valladolid y miembro de la Comisión de divulgación de la RSME. El ABCDARIO DE LAS MATEMÁTICAS es una sección que surge de la colaboración con la Comisión de Divulgación de la Real Sociedad Matemática Española (RSME) |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |