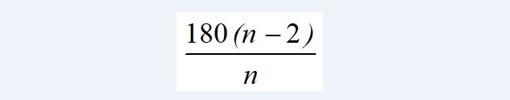Los secretos matemáticos del embaldosado
Los secretos matemáticos del embaldosado |
 |
 |
 |
|
ABC, 27 de Enero de 2020 Desde la Antigüedad, el ser humano ha utilizado diferentes motivos para adornar el pavimento. Y ha ideado diferentes modos de hacerlo
Embaldosado - Pixabay
Después de echar un vistazo a los cielos la semana pasada, volvamos al suelo que pisamos, porque las matemáticas también pueden decirnos algunas cosas. Nuestra ajetreada vida cotidiana no nos permite disfrutar de todo lo que nos rodea, o al menos pararnos a pensar en algún momento cómo son las cosas con las que convivimos. Con este artículo voy a comenzar una serie sobre cómo organizamos y configuramos algo de lo que no podemos prescindir (al menos por ahora): el suelo. Desde la antigüedad, el ser humano ha utilizado diferentes motivos para adornar el pavimento de calles y viviendas, para decorar paredes, techos y objetos como cajas, muebles, etc. Y ha ideado diferentes modos de hacerlo. Eso es de lo que vamos a hablar: cómo recubrir el plano, dicho en términos matemáticos. Por si el lenguaje puede resultar un inconveniente (muchas veces es lo que pasa en matemáticas; decimos que no entendemos por la jerga utilizada, pero en muchas ocasiones simplemente las ramas no nos dejan ver el bosque, y las cosas son más simples de lo que parecen; otras no, por supuesto). Utilizamos la expresión “el plano” para designar una superficie con dos dimensiones, largo y ancho. Esa palabra trata de responder al concepto intuitivo de todo aquello que es así, plano, que no tiene altura, o es irrelevante para lo que estamos haciendo. Son planas las paredes, los techos (aunque estén inclinados; eso no nos incumbe para lo que queremos tratar que es el recubrimiento de los mismos), una hoja de papel, y por supuesto, el suelo. Llamaremos mosaico o teselado del plano a un conjunto de piezas (baldosas o teselas) con las que trataremos de recubrir totalmente el plano, sin dejar ningún hueco, y sin montar o solapar unas piezas con otras. El que haya intentado embaldosar un cuarto de baño, una habitación irregular, etc., sabe por experiencia que la tarea no es trivial. No es trivial si se quiere hacer bien, claro. Si lo que queremos es acabar rápido, hacemos cachitos y vamos rellenando de cualquier manera. Pero ya sabéis que los matemáticos lo queremos perfecto, simétrico, que den ganas de mirarlo, no que nos espante la vista. Polígonos regularesHoy vamos a empezar por lo más sencillo: utilizando exclusivamente polígonos regulares (ya saben, triángulos, cuadrados, pentágonos, hexágonos, etc.). Ya lo iremos sofisticando más adelante. Ya saben que en matemáticas las cosas no se hacen al tun-tun (ensayo-error; a veces para intentar entender una situación, sí se puede probar, pero en asuntos tan sencillos como éste, pues no es necesario), así que vamos a echar una pequeña cuenta. Nos vamos a fijar en un hipotético vértice del embaldosado, es decir, en un punto en el que se juntan varias losetas de las que vamos a utilizar. Si desde ese punto trazamos una circunferencia con el compás, nos percataremos inmediatamente de que el plano se recorre completamente con esa circunferencia, puesto que encierra todos puntos alrededor de ese vértice. Es decir, que el plano se completa con 360º, que es la amplitud total de una circunferencia. A continuación, necesitamos saber los grados de cada uno de los ángulos de los polígonos regulares. Al ser regulares (es decir, todos los lados tienen la misma longitud), los ángulos son también iguales para cada polígono. En el colegio nos enseñaron en su momento que la suma de todos los ángulos de un polígono regular de n lados viene dada por la expresión: 180 (n-2) Así, para el triángulo (n = 3), la suma de todos los ángulos es 180º; para un cuadrado (n = 4), dicha suma es 360º; para un pentágono (n = 5), es 540º, y así sucesivamente. Si queremos saber la amplitud de cada ángulo, basta con dividir la expresión anterior entre n (el número de lados):
Dando valores, se obtiene que:
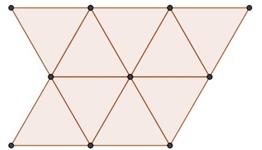
Como debemos repartir esos valores de los ángulos en 360º, sólo nos sirven aquellos que dividan a ese valor. Así, por ejemplo, para n = 3 (triángulos), podemos rellenar el suelo con seis losetas, porque 360 es divisible entre 60, y el cociente es 6. Así lo vemos en la siguiente imagen: en cada vértice (sólo aparecen todos en el central) se disponen seis triángulos.
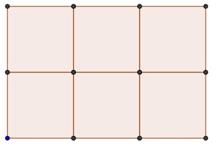
El siguiente valor que divide a 360º sería el de n = 4 (cuadrados), es decir, también rellenamos de forma regular el plano con cuatro cuadrados, porque 90 x 4 = 360.
Aquí encontraremos en nuestras calles variaciones, porque un suelo así sería monótono y aburrido (aunque los hay). Si desplazamos las filas un poco, eliminamos ligeramente esa sensación. En la siguiente imagen, que he tomado en una calle cercana a mi casa, observamos tanto en el suelo como en la pared, teselados con cuadrados (o rectángulos; da igual porque los ángulos siguen siendo de 90º). Sin embargo, en el suelo la disposición es diferente a la de la pared, en la que se contrapean tanto las hileras de ladrillo como las de color blanco. En el caso de la pared, esta acción da más solidez al conjunto (los que hemos jugado de pequeños a construir con el Exin Castillos o el Tente lo sabemos muy bien).
Otra variación del mismo teselado es jugar con las dos direcciones, horizontal y vertical, buscar simetrías, jugar con diferentes colores, etc., como vemos en las siguientes fotografías.
Volviendo a la tabla, solamente queda una posibilidad de embaldosar el plano con polígonos regulares e iguales: con hexágonos (n = 6), porque 120 x 3 = 360 (pueden comprobar que no hay más).
La segunda de las imágenes está tomada de un portal de una céntrica calle de Valladolid. Al teselado hexagonal se le han añadido dibujos y colores, pero observen que los mosaicos base son todos hexágonos. Por cierto, cuando van al fútbol o ven alguna imagen de un partido por televisión, ¿se han fijado en las redes de las porterías? ¿Obedecen a alguna de las disposiciones anteriores? ¿Dónde encontramos más teselados triangulares, cuadrados o hexagonales? Lo que saben las abejasLa verdad es que en este punto le dan a uno ganas de contarles cómo las abejas (como otros animales) saben más matemáticas de lo que imaginamos. Si no, ¿cómo se explican que hayan llegado a la conclusión de que el modo de almacenar más miel, sin desaprovechar el más pequeño espacio, y utilizando la menor cantidad posible de cera (que lo suyo les cuesta fabricarla) para construir el borde, es con panales hexagonales? Podrían haberlos hecho cuadrados, o triangulares, o con otra configuración, pero no, han utilizado la óptima. En fin, seguro que esto ya lo sabían.
Muchos profesores de matemáticas de todo el mundo (también en España) han venido utilizando desde hace ya tiempo como recurso didáctico para enseñar la materia y favorecer además la transversalidad con otras asignaturas (arte, historia, etc.) las denominadas rutas matemáticas por nuestros pueblos y ciudades. Mirar a nuestro alrededor con ojos matemáticos puede ayudar, suele ayudar, a comprender mejor las cosas, y a valorar la capacidad indudable de nuestros antepasados. Recientemente ha salido publicado un magnífico libro con ilustraciones y explicaciones a todo color (merece la pena; la primera edición se agotó en pocos días) titulado «Periplo por la geometría de Valladolid» (Inmaculada Fernández y Encarnación Reyes, Ayuntamiento de Valladolid) en el que a través de cinco capítulos, cada uno dedicado a un concepto matemático distinto, se van recorriendo calles y monumentos de la ciudad. Aunque pudiera pensarse que el interés es únicamente para los ciudadanos o visitantes de la ciudad, nada más lejos de la realidad, ya que incluye explicaciones y da pautas (muestra muchas de las cosas a localizar) para poder realizar trabajos similares por cualquier otro pueblo o ciudad. Continuará… Resolviendo cuestiones pasadasHace dos semanas dejaba propuestas dos cuestiones para los lectores. Una de ellas muy bien resuelta por uno de ellos (por tanto, a su explicación nos remitimos), y la otra, quizá más complicada y técnica, de la que nadie hizo mención. Resolvamos esa, recordando qué decía: 1.- Se eligen tres puntos cualesquiera A, B, C, sobre una circunferencia de radio unidad. Sea R el lugar geométrico definido por el ortocentro del triángulo ABC (es decir, la región del plano que forman todos los posibles ortocentros de todos los posibles triángulos ABC). Determinar el área de esa región R. Los ejercicios de lugares geométricos suelen atacarse mediante geometría analítica, es decir, meter coordenadas a los puntos y hala, a echar cuentas. Como pista, para que no lo intentaran de ese modo, les comenté que se puede resolver de un modo más rápido, gracias a la recta de Euler. En efecto, en vez de pensar en el ortocentro (llamémosle H) del triángulo, pongamos nuestra atención en los otros dos puntos que están sobre la recta de Euler, el baricentro (G) y el circuncentro (O). El circuncentro es, en la situación descrita, el centro del círculo, y el baricentro va a estar en cualquier lugar del círculo, pero en su interior. En el artículo se indicaba (sin demostrarlo) que siempre se cumple que HG = 2 GO, de modo que el ortocentro H va a tomar como máximo el valor 3 (vean el dibujo de la recta de Euler del anterior artículo). Por tanto, R va a ser el círculo de radio 3, y por consiguiente su área será 9π. Alfonso J. Población Sáez es profesor de la Universidad de Valladolid y miembro de la Comisión de divulgación de la RSME. El ABCDARIO DE LAS MATEMÁTICAS es una sección que surge de la colaboración con la Comisión de Divulgación de la Real Sociedad Matemática Española (RSME) |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |