¿Cuántas personas te pueden besar a la vez?
¿Cuántas personas te pueden besar a la vez? |
 |
 |
 |
|
ABC, 1 de Junio de 2020 La explicación detrás del término matemático «kissing number»
Fotolia
Esta maldita pandemia que nos ha asolado (no ha sido única a lo largo de la Historia como bien sabemos, pero, ¡qué demonios!, es la que nos ha tocado) nos ha traído muchas calamidades y contratiempos. Por supuesto, la salud de la población es lo primordial (cierto es que la economía, tanto la general como la particular va a sufrir un varapalo considerable, pero, qué quieren que les diga, sin personas, ninguna otra cosa es posible), pero también ha trastocado algunas de nuestras costumbres más connaturales, entre ellas abrazarnos y besarnos. En matemáticas existe un término que, en otras circunstancias, hubiéramos mirado con indiferencia y hasta reído de él, el kissing number (número de besos, traducido literalmente), ya que los besos entre personas nada tienen que ver con los que suceden entre objetos. Pero ahora que no “debemos”, al menos no indiscriminadamente, las cosas “pintan” de otro modo. Veamos cómo se besan, en concreto, las esferas.
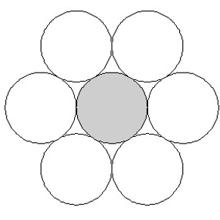
La cosa no es demasiado complicada: en el espacio de n dimensiones, el kissing number K(n) es el número máximo de esferas unidad (o sea de radio 1) disjuntas (es decir, esferas que no se cortan, que no tengan partes comunes) que pueden tocar a otra esfera dada. Veamos un ejemplo, para entenderlo mejor. Una esfera en el plano, es decir, en dos dimensiones, es una circunferencia. Fijémonos en una concreta, la que aparece en la imagen sombreada, de radio uno (las unidades, las que se quieran, centímetros, pulgadas, metros, da igual). El número máximo de otras circunferencias del mismo tamaño que la “besan” es claramente 6 en la disposición mostrada. Diríamos entonces que K(2) = 6. Claro que, para concluirlo, deberíamos probarlo para todas las configuraciones que pudiéramos realizar, no vale con afirmarlo para la primera que hemos imaginado. Pero vamos poco a poco, que esto sólo era un ejemplo para entender a que nos referimos con ese kissing number.
Por cierto, y antes de que los puristas se metan conmigo, digamos que en español tenemos un nombre para definir ese número, y desgraciadamente no es tan evocador. Aquí se denomina número de osculación. Sí, lo sé, he roto toda la magia de los besos, pero es lo que hay. En dimensión 1, o sea, en la recta real (todo el universo se reduce a una única recta), las esferas son puntos, y como sólo hay una dirección (pero dos sentidos; a la izquierda del punto, y a su derecha; en efecto, por si a alguien se le ocurre: tan simple, elemental y aburrido como nuestro arco parlamentario, y ya ven cómo andan, pegándose un día sí y otro también, cada uno en su posición sin moverse del sitio un ápice):
En el dibujo, la esfera es el punto de color rojo, y los azules, las otras dos que la “besan”, una a cada lado. Claramente tenemos que K(1) = 2.
Hasta aquí todo parece más o menos sencillo, pero, ¿qué pasa al ir a dimensión 3, a nuestro espacio tridimensional? ¿Cuántas esferas besan a la azul de la imagen? Parece que 12, pero el caso es que, queda bastante hueco vacio en esa configuración, y quizá se puedan poner de otro modo donde quepan más. Ese razonamiento fue en el que se apoyaba David Gregory (1659 – 1708) para afirmar que seguramente puedan ponerse de algún modo 13 esferas que besen a la azul. Pero un contemporáneo suyo, de nombre Isaac Newton (1642 – 1727), decía que para nada, que eran 12 el número máximo, y dio pie a una famosa discusión entre ellos el 4 de mayo de 1694. El argumento de
Newton era que, si nos fijamos en lo que pasa en dimensión dos (giramos un poco la configuración que pusimos arriba), por encima del diámetro de la circunferencia sombreada, tenemos tres circunferencias, y otras tres por debajo. Razonando por analogía, en el caso de la esfera tridimensional, podemos colocar seis esferas por encima de su ecuador, y sólo otras seis por debajo. Y esa estructura es tan clara y rígida que no cabe otra. Pero ya sabéis que, en matemáticas, si no hay una demostración formal, rigurosa y bien hecha, los argumentos no valen de nada, lo diga quien lo diga (y no hablamos precisamente de un mindundi). Los milagros en matemáticas (y diria que en nada, pero no quiero aguar la fiesta a nadie; Dios me libre) no existen, y el asunto llevó mucho tiempo y muchos intentos hasta que se resolvió. Incluso se bautizó el dilema: el problema de las trece esferas. El matemático alemán Reinhold Hoppe (1816 – 1900) pensó en 1874 que había resuelto el problema, pero se encontró un error en su razonamiento. Hubo que esperar al año 1953 para que el alemán, Kurt Schütte (1909 – 1998) y el holandés Bartel Leendert Van der Waerden (1903 – 1996) hicieran una demostración válida de que efectivamente K(3) = 12. Posteriomente, otros autores han simplificado y hecho más entendible su demostración. De hecho, hasta cinco demostraciones distintas han sido construidas desde entonces, enriqueciendo no sólo el tópico, sino aportando en ellas nuevos enfoques y resultados, aprovechables en otros temas y problemas. Es un ejemplo de cómo las matemáticas pueden expandir su conocimiento aún a partir de resultados conocidos, pero con técnicas diferentes. Una de ellas es la publicada por el norteamericano Oleg R. Musin mediante cálculo elemental y geometría esférica. Planteemos la situación desde una perspectiva diferente: si N esferas unitarias “besan” a una esfera unitaria en R^n, el conjunto de los puntos donde lo hacen es una disposición en torno a esa esfera central de modo que la distancia euclidea entre cualquier par de esos puntos de tangencia sea al menos 1. Con esa idea podemos entonces enunciar el asunto en términos de ángulos: ¿cuántos puntos pueden colocarse sobre la superficie de una esfera de modo que la separación angular entre dos cualesquiera de esos puntos sea al menos de 60º? (¿Sabrían deducir porque 60º? No es difícil). Curiosamente, hacia 1930, en un contexto diferente, se plantea otro asunto que se denominó el problema de los dictadores enemigos: ¿Dónde deberían N dictadores de un determinado planeta construir sus palacios para estar lo más lejos posible el uno del otro? Este problema de matemática discreta surge del botánico danés R. M. L. Tammes (en realidad, de acuerdo a su profesión, el asunto le vino a la mente en términos de cómo se distribuyen las aberturas de los granos de polen en diferentes tipos de flores). El problema se conoce también alternativamente como el problema de Tammes en su honor. El geómetra húngaro László Fejes Tóth (1915 – 2005) lo resolvió hacia 1943 para los valores de N = 3, 4, 6, 12; los citados K. Schütte y Van der Waerden para N = 5, 7, 8, 9; el alemán Ludwig Danzer (1927 – 2011) para N = 10 y 11; y el norteamericano Raphael Mitchel Robinson (1911 – 1945) para N = 24 en 1961 (este matemático estuvo casado con la célebre matemática Julia Robinson, de ahí su apellido, de quien hablaremos en otra ocasión). El primer valor para el que no está resuelto, N = 13, tiene relación estrecha con el problema de las trece esferas y la célebre conjetura de Kepler (hoy ya resuelta) de empaquetamiento de esferas. Hay un asunto, denominado el problema duro de las trece esferas, que, tal y como pretende transmitir el adjetivo añadido, complica un poco más el estudio: encontrar una disposición de trece esferas tridimensionales iguales que no se solapen (sólo se “besen”) determinando su radio (o sea, permitimos que el radio de ellas sea menor que el de la esfera a la que besan que mantendremos de radio unidad). Obviamente, como K(3) = 12, la solución de este nuevo problema implica que los puntos de tangencia estén a menos de 60º.
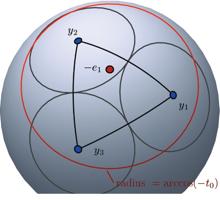
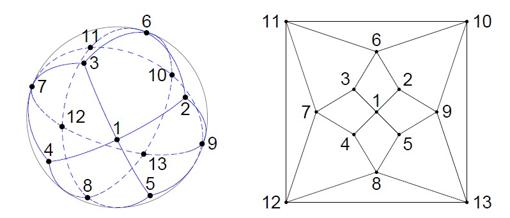
Los húngaros Károly Böröczky y L. Szabó demostraron hace no mucho, en 2003, que esa distancia debía ser estrictamente menor que 58.7º. Más recientemente aún, en 2008, la matemática francesa Christine Bachoc y el alemán Frank Vallentin, (obtuvieron por este trabajo en 2011 el prestigioso premio SIAG/Optimization) demostraron que incluso debía ser menor que 58.5º. Ya ven, ¡¡tuvieron que pasar cinco años para que la cota se mejorara en dos décimas!! Y nos podemos sentir afortunados: les recuerdo que pasaron 300 años para que se resolviera la discusión entre Newton y Gregory. En Ciencia el panorama es así, de modo que tengan paciencia con la vacuna del COVID – 19 que las perspectivas no parecen ser tan lejanas (esto a los politiquillos de tres al cuarto, la mayoría del mundo mundial, es una de las razones por las que seguramente no quieran invertir en investigación en ciencia; consideran que la inversión no compensa ante el hipotético éxito, pero, ¿tenemos una alternativa mejor?). Más cerca aún en el tiempo, en 2018, nuevamente el norteamericano Oleg Musin y el soviético Alexey S. Tarasov (¿ven como las matemáticas hacen conciliar hasta las más enfrentadas potencias?), han probado que la distancia entre dos puntos cualesquiera debe ser como mínimo de 57.1367º, y su demostración utiliza grafos irreducibles. En la imagen se muestra la disposición encontrada para la citada cota inferior y su grafo asociado.
Por cierto, y esto es de cosecha propia, ese grafo asociado, ¿no les recuerda nada? Seguramente no tenga nada que ver, pero a mí me recuerda a la planta de las naves de nuestras magníficas iglesias y catedrales. A lo mejor se podría hacer un estudio de dichas plantas mediante este tipo de grafos y se pudieran sacar algunas conclusiones, pero ya digo que, a lo mejor no tenga ningún sentido; es una idea que me viene alilo de la redacción de este artículo. La demostración del resultado anterior descansa completamente en el análisis de grafos del tipo del representado: estudio de su planaridad, del orden de sus vértices, de las propiedades combinatorias y geométricas de los vértices y las caras, y algo de trigonometría, aspectos técnicos que, por supuesto, quedan fuera del ámbito de este contexto. Acabaremos diciendo que el asunto de la búsqueda de los números de osculación en dimensiones mayores no está ni mucho menos cerrado, y es un problema pendiente de resolver. En dimensión 4, durante un tiempo se ignoró si la solución era 24 o 25, hasta que también Oleg Musin probó en 2003, que la solución correcta era K(4) = 24. Para valores n > 4, el problema sólo está resuelto en los casos K(8) = 240 y K(24) = 196560 gracias a los célebres Andrew Michael Odlyzko y Neil James Alexander Sloane en 1979. Para el resto de dimensiones hasta n = 24, sólo se tiene cotas inferiores y superiores. Por ejemplo, se sabe que 40 < K(5) < 45, 72 < K(5) < 78, etc. Bien, aquí tiene un nuevo reto con el que entretenerse cuando no sepan qué hacer (ganarán bastante dinero y fama, si lo resuelven). Ah, y por cierto, Newton y Gregory tuvieron a lo largo de su vida otras “enganchadas” (también los científicos se dicen de todo), pero eso lo dejaremos para otra ocasión . Alfonso J. Población Sáez es profesor de la Universidad de Valladolid y miembro de la Comisión de divulgación de la RSME. El ABCDARIO DE LAS MATEMÁTICAS es una sección que surge de la colaboración con la Comisión de Divulgación de la Real Sociedad Matemática Española (RSME) |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |