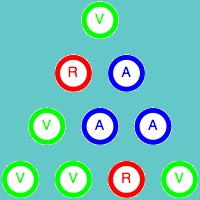
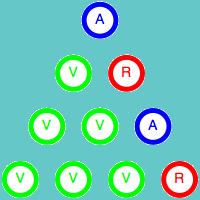
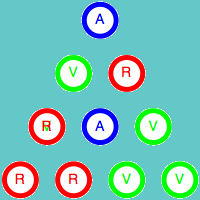
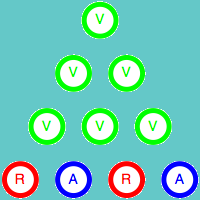
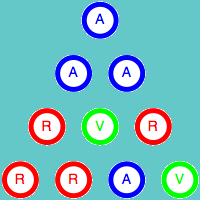
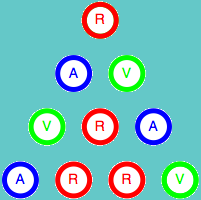
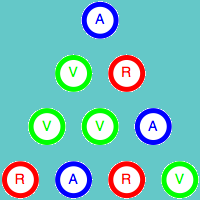
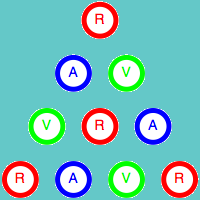
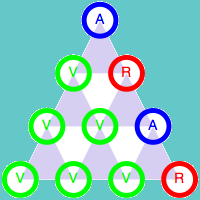
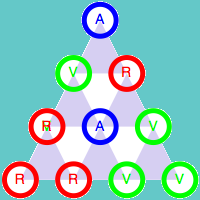
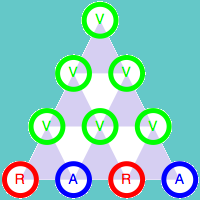
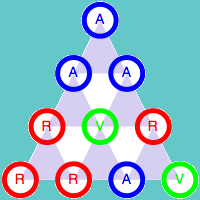
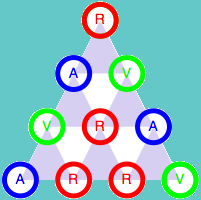
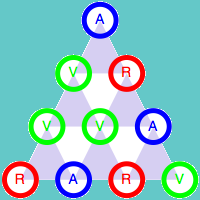
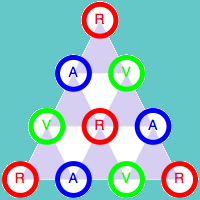
Como ya hemos indicado, el color de la esquina superior depende únicamente de los colores de las otras dos esquinas del triángulo. Esta propiedad es válida para cualquier triángulo de tamaño 3ⁿ+1.

Veamos la demostración para el caso n = 1, es decir para el triángulo de cuatro filas. Para ellos vamos a estudiar todas las combinaciones posibles de los colores de los cuatro elementos iniciales.

• Caso 1: los cuatro elementos del mismo color.

  
  Primera fila del mismo color

• Caso 2: tres elementos del mismo color.
  En este caso, sólo hay dos posibilidades (pues las demás se reducen a estas). Los resultados se ilustran en las siguientes figuras:

  Mismo color en las esquinas	Diferente color en las esquinas

• Caso 3: dos elementos del mismo color y sólo dos colores en la primera fila.
  En esta ocasión, todas las situaciones posibles se reducen a estas tres:

  Colores juntos dos a dos	Colores alternados	Mismo color en las esquinas

• Caso 4: dos elementos del mismo color y los tres colores en la primera fila.
  Ahora hay cuatro posibilidades, según la disposición relativa de los dos elementos del mismo color:

  Mismo color en una esquina	Mismo color en el centro	Un color intercalado	Mismo color en las esquinas

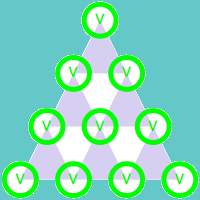
El siguiente caso donde los dos colores de la esquina inferior dan la información suficiente es el de 10 elementos en la primera fila. Para entender el resultado, basta imaginar el triángulo como superposición de seis triángulos con cuatro elementos en la fila inferior, los que ocupan las posiciones 1, 4, 7 y 10, que serán los cuatro elementos clave. De este modo, los casos anteriores completan la información.

• Caso 1: los cuatro elementos clave son del mismo color.

  
  Primera fila del mismo color

• Caso 2: tres elementos clave son del mismo color.

  Mismo color en las esquinas	Diferente color en las esquinas

• Caso 3: dos elementos clave son del mismo color y entre los cuatro sólo hay dos colores.

  Colores juntos dos a dos	Colores alternados	Mismo color en las esquinas

• Caso 4: dos elementos son del mismo color y están los tres colores entre los cuatro.

  Mismo color en una esquina	Mismo color en el centro	Un color intercalado	Mismo color en las esquinas

Mediante la superposición de triángulos de menor tamaño que cumplen la propiedad anterior se puede demostrar análogamente que la propiedad es válida para cualquier disposición inicial formada por 3ⁿ + 1 elementos.