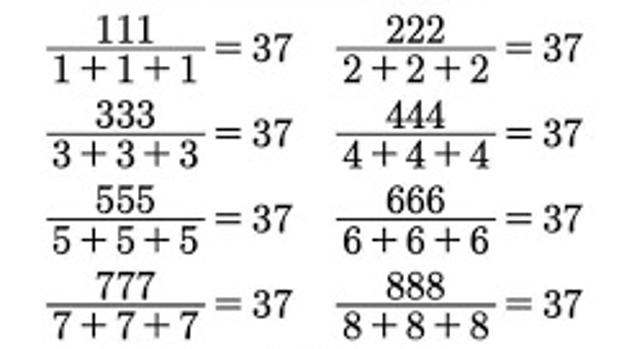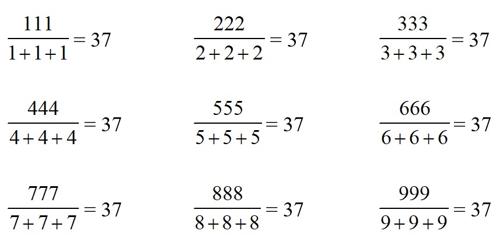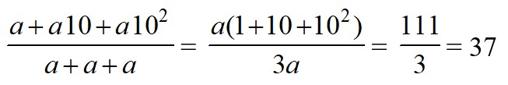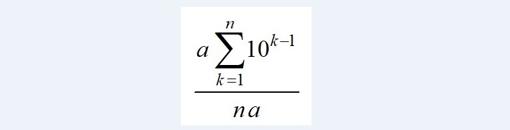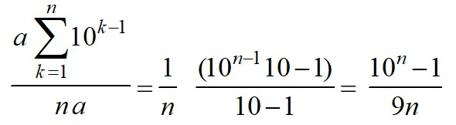El truco detrás del «misterioso» número 37 y otras fórmulas matemáticas virales
El truco detrás del «misterioso» número 37 y otras fórmulas matemáticas virales |
 |
 |
 |
|
ABC, 28 de Septiembre de 2020 Aunque muchos lo achaquen a razones que van desde la magia a la belleza, lo cierto es que la explicación no puede ser más racional
Las matemáticas son una materia compleja y a determinados niveles complicada. La complejidad radica en que tiene varias y muy diferentes vertientes. Por una parte está su carácter técnico (los algoritmos y resultados que nos permiten resolver ejercicios o problemas que se presentan con frecuencia en nuestra vida; lo único de lo que hemos tenido noticia en la etapa escolar y de un modo muy limitado), y por otra su propia concepción y construcción, mucho más próxima a la filosofía que a una ciencia experimental. Aunque predomine una de esas dos facetas, no dejaremos de incluir aquello que nos parezca asequible de ambas, en un intento de que el lector conozca un poco mejor esta disciplina, y descubra que no consiste sólo en “echar cuentas” sin mayor alcance. Es habitual escuchar la excusa de no entender las matemáticas. Como con todo en esta vida, la dificultad de los niveles es variable, depende de cada persona y de muchos factores, como el interés que uno tenga, cómo y quién nos enseñe, etc.; el menos determinante, aunque no se lo crean, es la capacidad intelectual. Soy de los que piensan que cualquier persona con una inteligencia media normal puede aprender cualquier cosa: unos lo harán en tres segundos, otros en cinco horas y otros en una semana, pero con tesón e interés, se logra. Lo que suele fallarnos es precisamente el interés. Por tanto, ante cualquier texto (de cualquier materia) coexistirán diferentes niveles de lectura y profundización. Cada cual debe quedarse en el que le interese.
Por poner un ejemplo concreto, es habitual encontrar en redes sociales expresiones como la de la imagen, seguidas de alguna expresión de asombro tipo “Magia”, “La belleza de las matemáticas”, u otras similares para calificarlas.
No sé lo que hacen otros compañeros ante imágenes así (que abundan). Sospecho que pasar de ellas esbozando media sonrisa. En mi caso, como mi cabeza cada vez tiene menos hueco libre para aventuras calculistas, eché mano de un papel y un bolígrafo, y garabateé unas cuentas:
En definitiva, para cualquier dígito a no nulo (si no, no hubiéramos podido simplificar la segunda fracción), el valor siempre es el mismo, no existe magia alguna (como en ninguna otra parte). Respecto a lo de la belleza, es obviamente una apreciación totalmente subjetiva. Más interesante puede ser la cuestión derivada de esta particularidad de los números de tres cifras: ¿existirán igualdades similares para números con otro número de cifras? Uno puede ponerse a comprobar casos concretos, como hemos hecho en este caso, pero una de las peculiaridades de las matemáticas (y de los matemáticos, por tanto) es que nos gusta saber que pasa siempre, en general, sea cuál sea el número de cifras (por eso demostramos proposiciones, lemas, teoremas, etc.). ¿Se les ocurre cómo podríamos hacerlo en este caso? Es evidente que en el numerador de esas fracciones tenemos un número de n cifras iguales. Esos números podemos representarlos en general con una suma del tipo
y los denominadores serían de la forma a∙n. Observen que n representa el número de cifras. En el caso anterior, n es igual a 3, ya que eran números de tres cifras. Una forma general de describir ese caso particular sería mediante la expresión
¿Por qué ese exponente k – 1? No es demasiado complicado ver que un número de una sola cifra no necesita ninguna potencia de diez, que uno de dos cifras necesita exponente uno para las potencias de diez (a + 10 b), y así sucesivamente. Es decir que los exponentes del diez son una unidad menores que el número de cifras del número. Este es un asunto vital para estudiar matemáticas: por muy fácil que aparente algo, si no lo entiendo, no sigo adelante, porque en caso contrario, la bola de la permisividad va creciendo, creciendo, …, hasta que me explota en las narices (o séase, no me entero de nada). Esto no es como algunas novelas o películas en las que desconecto cinco páginas (o media hora de metraje) y no importa porque luego me lo vuelven a recordar o a resumir. No. Aquí como te despistes en una coma, las consecuencias se pagan. Como acabamos de decir, muchos textos matemáticos, científicos, etc., tienen diferentes niveles de profundidad. Puedo no estar interesado más que en la conclusión, o puede que me pierda y no entienda nada a partir de cierto momento. En un texto técnico, eso no tiene remedio; en uno de divulgación, uno puede decidir hasta qué punto profundizar y qué cosas saltarse. No va a importar porque en algún momento el autor me va a hacer lo que esos libros o películas mencionados: me lo va a resumir en ideas generales de un modo más asequible. Aquí empieza esa parte más técnica de esta reseña (que es de 2º de ESO, no crean que va mucho más allá): deberíamos recordar una fórmula que nos dice cómo sumar la expresión del numerador anterior (es la suma de los primeros sumandos de una progresión geométrica, por si alguien quiere buscarlo en el libro de sus hijos). La aplicamos:
Necesitamos finalmente que esas fracciones correspondan a un número natural (para que quede “bonito”, para que “haya magia”). No es difícil razonar cuándo sucede eso (con las reglas de divisibilidad prácticamente se determina), pero como veo ya a alguno que se empieza a cansar, cojamos el ordenador (un gran aliado para los matemáticos en los tiempos actuales), y demos algunos valores a n, por ejemplo, desde 1 hasta 10:
Nos aparece el caso de una cifra (trivial), el de tres (el comentado anteriormente), pero, ¡¡ojo!! Con nueve dígitos, ¡¡también obtenemos un número natural!! ¿No les suena? Seguro que los amantes de esas fórmulas “curiosas” y “bellas” lo han identificado ipso facto. Responde a aquella otra imagen “mágica” de los números tantas veces reproducida:
Observen que el número que se repite es el múltiplo de 9 que ponemos en el primer miembro de la multiplicación. ¡¡Ah!! ¡¡La magia, de nuevo!! Pues ya ven por donde que no, que no es magia. Es el mismo truco que nos le endosan dos veces como si fueran dos cosas distintas. A todo esto, confío en que no se nos enfaden dos de nuestros colaboradores habituales, fantásticos matemagos, con tanto sarcasmo sobre la magia. La “magia” es genial como motivación, no como creencia o engañabobos. Esto enlaza con otra característica de las matemáticas: si no hay demostración (y bien hecha, sin pufos), sencillamente no perdemos el tiempo. En nuestra sobre-informada e informatizada sociedad campan a sus anchas (y cada vez con mayor “éxito”) todo tipo de pseudociencias, afirmaciones gratuitas y majaderías varias. Las matemáticas y los matemáticos nos ayudan a conformar nuestros modos de pensamiento de un modo lógico y racional, y cuando se tercie así lo pondremos de manifiesto. Cualquier creencia es respetable (siempre que no atente contra la dignidad y libertad humana), pero puede y debe ser analizada, y luego cada cual que piense lo que quiera, pero no es aceptable permitir que algún desaprensivo se aproveche de nadie. El matemático es no sólo escéptico con los escépticos, sino con los propios compañeros de profesión, cuanto más con los caraduras. Es uno más de los aspectos formativos de esta disciplina. Nuevo curso, nueva ilusiónComo en cursos anteriores (parece mentira, pero llevamos ya la friolera de 130 entradas y 4 videos), además de hablar sobre aplicaciones prácticas de las matemáticas y los conceptos en los que se basan, seguiremos con la historia y biografía de algunos de sus investigadores (humanizar la ciencia es fundamental: son personas como nosotros las que desarrollan el conocimiento. Los resultados no aparecen porque sí, por generación espontánea, ni han sido revelados por quien sabe quién; surgen del trabajo y el análisis de los problemas a resolver), tratando de desmenuzar los problemas que permanecen abiertos sin solución, algunos desde hace siglos; y los asuntos de actualidad en los que las matemáticas tengan algo (o mucho) que aportar. No olvidaremos tampoco los eventos matemáticos que se celebren en todo el planeta que puedan aportarnos algo interesante. Cada año hay cientos de ellos, la mayoría son muy técnicos y especializados, pero algunos, por ejemplo, los relacionados con la educación y la divulgación, pueden tener cabida.
El pasado 14 de marzo, cuando comenzó el confinamiento, no pudimos celebrar el Día Internacional de las Matemáticas como nos hubiera gustado (recordarán por qué ese día: acuérdense de los primeros dígitos del número pi). Pero no sabe el dichoso virus con quien está tratando: este año próximo 2021 todo el mes de marzo (y algunos días puntuales previos para ir creando ambiente), tendremos un montón de sorpresas matemáticas para todos. Todo ello escrito del modo más asequible que podamos, con algunas dosis de humor, y en algún caso, también algo de mala uva. Pero siempre desde el respeto, el mismo que los lectores nos vienen mostrando con sus aportaciones en los comentarios, lo que agradecemos enormemente en estos tiempos de verborrea irracional, vacía y mediocre. En matemáticas tales comportamientos no caben. Tradicionalmente, las matemáticas no es que hayan sido de un agrado universal precisamente, en particular en nuestro país. Hace no mucho, mirábamos de reojo con cierta sana envidia, la magnífica divulgación matemática de prácticamente todos los países desarrollados. A día de hoy esto ha cambiado afortunadamente mucho, tanto que hay decenas de sitios y recursos, la mayoría además muy bien planteados y desarrollados, con los que disfrutar de las matemáticas. Fenomenal, aunque conlleva algunos inconvenientes: la mayor parte de los temas atractivos y asequibles han sido tratados con profusión. Por eso muchas veces encontrarán en todos estos lugares (aquí también) asuntos y argumentos ya descritos. Intentaremos dar nuestro toquecito original, pero entiendan que no es fácil. En cualquier caso, ninguno está de más. Y para acabar, agradecer a la Real Sociedad Matemática Española el apoyo y la labor constante de difusión de esta disciplina desde 1911, y al diario ABC por acoger un año más esta sección, y a sus redactores por la infinita paciencia con nuestras “pequeñas manías” con la precisión y la corrección. Os esperamos cada lunes (o martes en alguna ocasión), y ojalá acertemos con las propuestas que vayamos haciendo. Sean todos bienvenidos. Posdata. Aquí tienen una “nueva” ristra de “magia” que seguro que no han visto por ninguna parte (la subiré a redes sociales, y ya verán cuánto tarda en multiplicarse sin mención a este artículo). Pero si han entendido bien esta reseña, descubrirán que es más de lo mismo, e incluso ustedes pueden encontrar más (y aún de más cifras; aquí son 27, para que no pierdan el tiempo en contarlas).
Alfonso J. Población Sáez es profesor de la Universidad de Valladolid y miembro de la Comisión de divulgación de la RSME. El ABCDARIO DE LAS MATEMÁTICAS es una sección que surge de la colaboración con la Comisión de Divulgación de la Real Sociedad Matemática Española (RSME) |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |