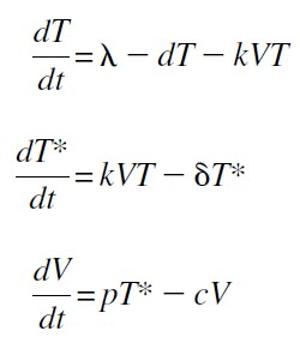Y esto, ¿para qué sirve?
Y esto, ¿para qué sirve? |
 |
 |
 |
|
ABC, 22 de Febrero de 2021 El autor explica cómo detrás de una ecuación puede estar la clave para conocer la evolución de un tumor o administrar una nueva vacuna, aunque el matemático que la resuelva ni siquiera lo sepa
AdobeStock
Cuando asistimos a alguna conferencia o una clase de matemáticas, es bastante común preguntarnos para qué servirá todo eso que, normalmente con cierta pasión, relata el profesor de turno. En estos pequeños relatos que vamos escribiendo cada semana, también aparecen con cierta frecuencia comentarios similares. Se sigue pensando en el matemático como alguien que vive en su mundo haciendo cosas inútiles (en el científico en general, aunque con esto de la pandemia, algunos han descubierto un poco algún sentido a tanto esfuerzo aparentemente tan poco rentable; rentable a corto plazo, debemos recalcar, porque lo desconocido no se desvela en un 'aquí te pillo, aquí te mato', en que la sociedad actual quiere convertirlo todo). Desde luego no se puede negar que una gran parte de que se tenga esa equivocada percepción es nuestra, bien sea por no valorar el esfuerzo que implica transmitir nuestros trabajos al resto de los mortales de un modo entendible, bien por la soberbia de 'esforzaos y aprended que lo suyo me costó a mí' (argumento casi residual en la actualidad afortunadamente, por la cuenta que nos trae), u otras espúreas razones. El caso es que lo que percibe el personal es en muchos casos una pizarra en la que el ponente escribe algo así
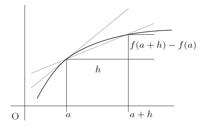
y prosigue describiendo cómo ha intentado resolver esa ecuación, para seguramente acabar al cabo de una hora larga diciendo que todos esos intentos no han llegado a ninguna parte y que tratará de aplicarle un método numérico cuyos avances nos contará dentro de, ¿seis meses? ¿tres años? Tiempo que dedicará, día tras día, a rellenar folios, implementar simulaciones en el ordenador, etc., etc., aparentemente ajeno al mundo. Lo que no se cuenta, es que, quizá detrás de la resolución de esa ecuación diferencial esté la clave para conocer la evolución de un tumor cancerígeno, o cómo administrar eficazmente y sin riesgos para los enfermos una nueva vacuna, o prever la propagación de un incendio en un bosque de difícil acceso. Más aún, seguramente el matemático que está tratando de resolver esa ecuación tampoco lo sepa. Porque no es su cometido. El conocimiento científico está en la actualidad tan segmentado, tan diversificado, que es materialmente imposible que todos conozcan lo que hace el resto de la cadena investigadora, simplemente por cuestión de tiempo: si tratar de buscar un procedimiento que resuelva la igualdad puede llevar años (o incluso no poder resolverla nunca, como sucede con un montón de enigmas planteados desde hace siglos; eso si son enigmas, y no las tonterías que se escuchan por ahí, que seguramente no pasen de meras anécdotas, casualidades o invenciones de gentes sin nada mejor que hacer y que pretenden dejar su nombre para la posteridad en base a nada. El 'aquí te pillo, aquí te mato' de antes nuevamente omnipresente, y en época de redes sociales, más). Entonces, ¿cómo voy a perder un tiempo que no tengo en ponerme al día de tal fenómeno físico, médico o de la disciplina que sea? E igual el resto respecto a las matemáticas, por supuesto. Afortunadamente, cada vez más y mejor, aparecen personas, publicaciones, medios de comunicación que tratan de poner un poco de claridad en el funcionamiento de estas cosas. Pero también hay que pedir al lector un poco de colaboración y confianza en el sentido de asumir la pertinencia y utilidad de todos esos trabajos e investigaciones, aunque no acabe de entender muchas de las cosas que nos cuentan. Sirva esta pequeña y probablemente imperfecta introducción para describir en qué consisten y que llevan detrás igualdades como la descrita arriba (y de paso satisfacer un poco al lector que hace unas semanas nos indicaba, con razón, que hay más en las matemáticas que la teoría de números, la geometría o los conceptos más elementales). EcuacionesTodos conocemos del colegio lo que es una ecuación. Se trata de una igualdad en la que hay un valor desconocido que queremos averiguar, y lo conseguimos en base a unas operaciones algebraicas perfectamente determinadas que son las que aprendemos y con las que nos tiramos toda nuestra etapa escolar muchas veces sin encontrarle mayor utilidad que averiguar el número de conejos, gallinas y demás habitantes de una idílica granja. Recordamos además que, según el exponente de la incógnita, o del número de igualdades que tengamos, las ecuaciones se clasifican en distintos tipos, cada cual con un procedimiento diferente de resolución. Si avanzamos lo suficiente en nuestra trayectoria escolar, también nos encontramos en algún momento con algo denominado derivada. Si nos lo explicaron como debe ser y/o lo entendimos bien (atención al y/o porque según cada cual puede ser una cosa, la otra, ambas, o ninguna; en matemáticas es muy importante el lenguaje, y saber interpretarlo), el concepto de derivada resuelve dos de los problemas más importantes planteados allá por el siglo XVII: el cálculo de la velocidad instantánea en Física, y el de la pendiente de la recta tangente a una función en un punto en Matemáticas. Dos asuntos aparentemente sin conexión que se resolvieron con el mismo concepto. En la gráfica, vemos una función f (en negrita), y queremos calcular la pendiente de la recta tangente en el punto a. Si trazamos la recta secante que pasa por los puntos (a, f(a)) y (a + h, f(a + h)), su pendiente viene dado por el cociente
que es la razón entre las imágenes de f (que para el que ya sepa algo de ecuaciones diferenciales responde a la variable dependiente), y sus abscisas (los valores correspondientes en el eje OX, a + h – a = h; la variable independiente). Si hacemos esa h cada vez más pequeña (obsérvese el dibujo), a + h se va aproximando al punto a. Cuando coincidan, es decir cuando h tienda a cero, en vez de una secante, tendremos la recta tangente a f en el punto a. Por esa razón, la pendiente de la recta tangente se va a definir como
y a ese valor le llamamos derivada de f en el punto a. Se denota por f ′(a). Obsérvese que esta idea tan aparentemente sencilla no ha podido ser rigurosamente descrita hasta la correcta definición del concepto de límite, lo cual no sucedió hasta el siglo XVIII. Newton, Leibniz y sus contemporáneos del XVII montaban unas expresiones muy complicadas para expresar esta idea, porque no tenían ese concepto, el de límite, del que nosotros hoy nos valemos, y mucho, para simplificar muchos cálculos. Si se han fijado, para describir esto de la derivada, hemos utilizado una idea dinámica, con movimiento: hemos dicho que «desplazábamos» las secantes hasta que «llegaran» a la recta tangente. Además, hemos dicho que para los físicos la derivada fue la solución al cálculo de la velocidad instantánea. Es decir, la derivada va asociada a todo proceso dinámico, en evolución, en movimiento. Y a nuestro alrededor estamos rodeados de circunstancias en movimiento. Nuestra propia vida es movimiento: pasado, presente y futuro. Una ecuación diferencial, como las ecuaciones que conocemos, es una igualdad en la que queremos averiguar algo desconocido. Eso por lo que corresponde al nombre «ecuación». Lo que atañe al apellido «diferencial», involucra a las derivadas. Es decir, una ecuación diferencial ordinaria (abreviadamente EDO), es una ecuación en la que aparecen derivadas de funciones y las variables sobre las que actúan esas funciones. Las primeras son las variables dependientes de la ecuación (porque “dependen” de otras), y las segundas las variables independientes (las situadas en el eje OX, ¿recuerdan?). Resolver una ecuación diferencial es encontrar la expresión de la función que cumple la igualdad. Por ejemplo,
es una EDO, en la que la variable dependiente es la y (porque depende de x), y la variable independiente es la x. Resolver la EDO es encontrar la expresión concreta de la función y. En este caso, la solución será cualquier función de la forma
porque si calculamos su derivada, obtenemos lo que aparecía en el segundo miembro de la EDO, es decir, 2x + 1. Obsérvese que hay infinitas funciones que cumplen la EDO, tantas como constantes Cte, que es cualquier número real que pongamos (vale cualquier constante porque la derivada de una constante es siempre cero). Igual que hay ecuaciones de primer, segundo, tercer grado, etcétera, las EDOs son del grado que indique la derivada. En el caso anterior era una EDO de primer orden, porque aparece una derivada primera. Si hubiera habido una derivada segunda, sería de segundo orden, y así sucesivamente. Por otro lado, a los matemáticos nos gusta no emborronar las expresiones demasiado, que sean lo más concisas posibles (aun así, seguimos espantando, pero bueno, que sepan que se intenta), por lo que la EDO anterior no se hubiera escrito como ven, sino así: y ′ = 2x + 1 Sabemos que la que lleve la derivada (el apóstrofo, la comita elevada) es la variable dependiente, y la que no tenga la derivada, la independiente, o sea, la x. Por eso, ¿para qué el paréntesis y la x del primer miembro? Hay muchas expresiones equivalentes para describir la derivada. Por eso tampoco es raro (de hecho, es muy común, sobre todo en Física, en Química y en disciplinas relacionadas con la salud) que la EDO anterior aparezca así:
Se lee “derivada de y respecto a x”. Queda aún más claro cuál es la variable dependiente y cuál la independiente. Y como las EDOs aparecen muchísimas veces en un contexto físico, la variable independiente, en vez de x, suele ser el tiempo, por lo que, en esos casos, se representa como t:
Esta EDO describe entonces la velocidad que lleva un móvil (no de los telefónicos, sino de los que se mueven, un coche, un niño que corre, la mano que te va a dar un sopapo, etc.). De la ecuación se deduce que describe un movimiento uniformemente acelerado (porque la aceleración es constante, es 2, que es la derivada de la velocidad respecto al tiempo, y correspondería a la derivada segunda
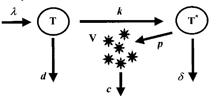
Volvamos al principio. Observen la primera EDO que escribí. Les voy a explicar qué es, como idea final. Vean esta imagen:
Representa el modelo básico para analizar la disminución de la carga viral del VIH (virus de la inmunodeficiencia humana; en efecto, el que desemboca en el SIDA) bajo tratamiento. Comenzamos considerando un modelo del ciclo de vida del virus. Aunque el VIH infecta diferentes tipos de células, con tasas de replicación variables, existe un consenso en que la mayor parte de la producción de VIH ocurre en las células T CD4 + activadas (son un tipo de células T que juegan un papel muy importante en el sistema inmunitario, en particular en el sistema inmunitario adaptativo). Por tanto, un modelo básico de infección por VIH solo incluye células activadas (T), células infectadas productivamente (T*) y libres de virus (V). Se supone que las células se activan a una tasa constante λ (lambda), y mueren con una tasa d por celda. En los individuos no infectados, durante la mayor parte del tiempo, hay un nivel constante de estas células, que viene dado por λ/d. Sin embargo, en pacientes infectados, estas células son susceptibles a la infección por VIH en una tasa proporcional al número disponible de células no infectadas y libres de virus, con una tasa constante k. De este modo, las células se infectan a una velocidad kVT, que corresponde a un comportamiento en masa (cuando una gran cantidad de individuos, células en este caso, se comportan todas a la vez como si lo hicieran de forma individual y sin coordinación), común en cinética química. Las células infectadas se crean a este mismo ritmo y mueren a un ritmo δ(delta) por célula, que puede ser diferente de la tasa de mortalidad de las células no infectadas (d), posiblemente mayor. Finalmente, el virus se produce de las células infectadas a una tasa p, y se eliminan de la circulación a una velocidad c. Eso es lo que representa el esquema de la imagen anterior. Pues bien, las ecuaciones correspondientes son:
A los matemáticos, aparte de interpretar el comportamiento anterior llegando a esta modelización en ecuaciones, lo que nos atañe es tratar de resolverlo (no lo he dicho, pero hay muchas, pero muchas EDOs que a día de hoy no se saben resolver de forma exacta), y una vez hecho, transmitir a los expertos el significado de esa solución. En efecto, sólo nos ven haciendo cálculos, pruebas con el ordenador, llenando folios. Pero detrás de eso, puede estar lo que acabo de contar (es un ejemplo de tantos). Esto lo he sacado de un artículo real, no es un ejemplo 'bonito' con los que nos recreamos y lucimos en clase (véase la bibliografía). Con estos análisis, fue posible cuantificar la rapidez de infección y replicación del VIH, la tasa de eliminación del virión (se llama así a la partícula vírica morfológicamente completa e infecciosa), la vida útil de las células infectadas de forma productiva, y predecir el impacto del tratamiento y la aparición de mutaciones resistentes a los fármacos. Además, esos modelos ayudaron a aclarar cuestiones controvertidas relacionadas con el mecanismo de agotamiento de células T en la infección por VIH y motivó nuevos estudios experimentales y clínicos. Así que, por favor, cuando vean a los matemáticos (a los científicos en general) en su mundo, ensimismados con cientos de folios rellenos de ecuaciones, sepan que andan detrás de cosas como éstas (y si son estudios teóricos, buscando soluciones a problemas que no se conocen y que, sin aplicación inmediata a corto plazo, puede que la tengan en un futuro, como ha sucedió muchas veces a lo largo de la historia), y hagan el favor de ahorrarse el cansino «y esto, ¿para qué sirve?». Bibliografía: Ribeiro, R. M.; Perelson, A. S. The Analysis of HIV Dynamics Using Mathematical Models, capítulo del volumen AIDS and Other Manifestations of HIV Infection, Elsevier (EE. UU), 2004. Alfonso J. Población Sáez es profesor de la Universidad de Valladolid y miembro de la Comisión de divulgación de la RSME. El ABCDARIO DE LAS MATEMÁTICAS es una sección que surge de la colaboración con la Comisión de Divulgación de la Real Sociedad Matemática Española (RSME) |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |