¿Pueden las matemáticas resolver un crimen?
¿Pueden las matemáticas resolver un crimen? |
 |
 |
 |
|
ABC, 17 de Enero de 2022
En esta nueva entrada del ABCdario de las Matemáticas se reta al lector a resolver un crimen al más puro estilo Sherlock Holmes
Aprovechando el tiempo extra que permiten las vacaciones de navidad decidí leer un precioso libro que hacía tiempo que tenía esperándome: 'Matemáticas y literatura' de la genial matemática y divulgadora Marta Macho Stadler. Este libro, el cual recomiendo encarecidamente, ahonda en las relaciones que existen entre estas dos disciplinas, normalmente consideradas como muy alejadas tanto en contenidos como en sus técnicas de trabajo. Sin embargo, tal y como se puede apreciar a lo largo de la lectura del mismo, no son pocas las ocasiones en las que la literatura bebe de contenidos propios de las matemáticas; tanto para sus tramas, generalmente en novelas de misterio o policíacas, como en el uso de estructuras numéricas que deben cumplir ciertas rimas, como, por ejemplo, las sextinas.
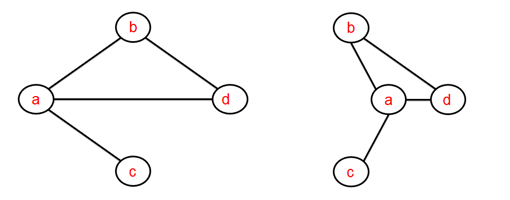
Por otra parte, en cuanto a la metodología de trabajo, matemáticas y literatura tienden a verse como actividades intelectuales con características tremendamente diferentes. Sin embargo, tal y como expresa la propia autora, y un servidor comparte, no distan tanto como solemos creer: «La percepción mayoritaria es que las matemáticas son frías, se deducen a partir de reglas establecidas y dejan poco espacio para la imaginación. También se piensa que la literatura surge exclusivamente de la creatividad, de la inspiración, de la emoción. Sin embargo, […] las matemáticas requieren de grandes dosis de ingenio y de intuición. […] Y en literatura, las letras no surgen únicamente por impulsos creativos; es necesario planificar y estructurar para que una buena historia se traduzca en un buen texto». (Macho Stadler, 2021, p.9). A pesar de lo que pueda parecer, la entrada de esta semana del ABCdario de las matemáticas no va a versar sobre la relación entre matemáticas y literatura, sino sobre un ejemplo concreto encontrado en el libro de Macho Stadler que relaciona ambas disciplinas: la novela policíaca 'Qui a tué le duc de Densmore?' (¿Quién mato al duque de Densmore?) del escritor y matemático Claude Berge. En dicha novela se relata un crimen que es resuelto por un matemático sin más que utilizar una rama concreta de las matemáticas, la teoría de grafos. Hablemos un poco sobre teoría de grafosLa teoría de grafos es una rama de las matemáticas que se dedica al estudio de las propiedades y resultados relacionados con unos objetos conocidos como grafos. Pero, ¿qué es un grafo? Un grafo G es un conjunto formado por dos tipos de objetos: vértices V y aristas E, donde estos últimos son en verdad pares de vértices. Así, un grafo G = (V, E) se puede describir a través de los vértices y aristas que lo forman. Por ejemplo un grafo G 1 = (V, E) puede expresarse determinando sus vértices V = {a, b, c, d} y sus aristas E = {(a,b), (a,c), (a,d), (b,d)}. Del mismo modo este grafo se puede representar de forma gráfica dibujando cada vértice como un punto y cada arista como un segmento que une dos vértices; de este modo dos representaciones gráficas de G 1 serían:
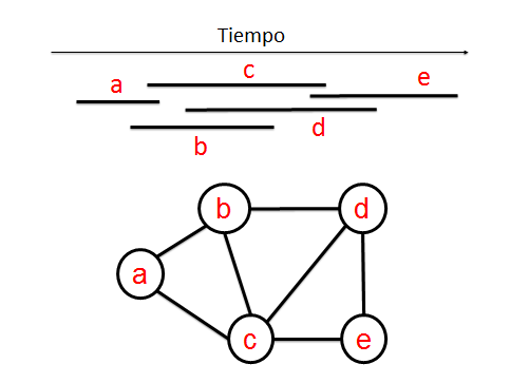
Figura 2. Distintas representaciones del grafo G 1 Cabe destacar que cualquier deformación continua aplicada a la representación del grafo es también una representación del mismo grafo, siempre y cuando las conexiones entre los vértices se mantengan. La teoría de grafos es de esas ramas de las matemáticas cuya importancia sobrepasa las matemáticas ya que sus objetos de estudio -los grafos- sirven para modelizar situaciones de diferentes disciplinas como química, transporte, biología, redes sociales, información y comunicación, circuitos y redes de ordenadores entre otros. Pero, ¿puede el estudio de los grafos ayudarnos a resolver un crimen? Un crimen resuelto usando teoría de grafosTal y como se describe en la novela de Claude Berge, dos policías de Scotland Yard intentan resolver un crimen acontecido en la isla de White. En dicha isla han aparecido dos muertos: Jeremy Morse –duque de Densmore- y su mayordomo Stewart. Desde un primer momento se sospecha del mayordomo -un clásico donde los haya-, pero de todos modos los policías investigan a todas las personas que han pasado por la isla en el último año sin llegar a conseguir determinar la culpabilidad de ninguna de ellas. Más adelante uno de los policías se encuentra con un colega matemático. Tras describirle este suceso y las declaraciones de los sospechosos, el matemático dibuja un grafo en el que cada persona es representada por un vértice y cada arista dibujada representa el hecho de que las dos personas unidas por dicha arista han coincidido en la isla. Este grafo dibujado por el matemático es lo que se conoce como grafo de intervalos y utilizando algunas propiedades de los mismos es capaz de averiguar que una de las sospechosas debería haber coincidido con más personas en la isla, hecho que denota que en verdad ha pasado algunos periodos escondida en la isla, momentos que en verdad ha utilizado para preparar su macabro asesinato. Grafo de intervalosSi representamos varios intervalos en una recta real, por ejemplo, podemos pensar en los periodos de tiempo que unas ciertas personas han pasado en una isla (ver figura 3). El grafo de dichos intervalos es aquel que se obtiene dibujando un vértice por cada intervalo o persona, y dos vértices se unirán con una arista si las personas que representan han coincidido en la isla o lo que es lo mismo si los correspondientes intervalos se intersecan (ver figura 3).
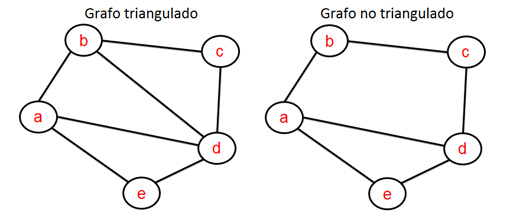
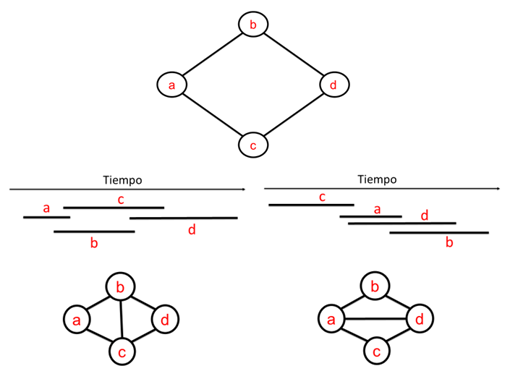
Figura 3. Intervalos y su correspondiente grafo de intervalos Los grafos de intervalos tienen propiedades interesantes, algunas de las cuales aparecen en la novela de Berge y permiten al matemático de la obra resolver el crimen. Hoy nos centraremos en la siguiente: Un grafo de intervalos siempre está triangulado. Un grafo se dice que está triangulado si para todo camino cerrado (conjunto de aristas consecutivas que comienza y acaba en un mismo vértice) formado por al menos cuatro aristas, existe al menos una que une vértices no consecutivos (ver figura 4).
Figura 4: Grafo triangulado, grafo no triangulado La demostración de esta propiedad no se presentará aquí, pero se puede encontrar en manuales sobre teoría de grafos. Sin embargo, una justificación informal de la misma es fácil de presentar. Si suponemos que existe un grafo de intervalos con un camino cerrado de longitud cuatro y que no está triangulado, al tratar de construir los correspondientes intervalos que dan lugar a dicho grafo vemos que un tal grafo no puede existir (ver figura 5).
Figura 5. Grafo de intervalos no realizable Conocidas estas pinceladas de teoría de grafos se reta al lector intrépido a convertirse en inspector matemático para resolver el siguiente crimen. Un nuevo crimen por resolverAcababa de llegar la primavera y la veterana inspectora Alicia Pelegrina de la Policía Nacional se encontraba ante un paisaje plagado de nieve. A su lado, su joven ayudante, el agente Jorge Martín. A pesar de sus años de experiencia, la inspectora Pelegrina jamás había visto un caso parecido. Una mujer, Araceli, había sido hallada muerta en la casa que habitaba en un abandonado pueblo del Pirineo aragonés del que era la única habitante. Las investigaciones permiten concluir a los agentes Pelegrina y Martín que el crimen se ha producido debido a un escape de gas venenoso accionado con un temporizador. El dispositivo, que había sido minuciosamente instalado, se encontraba escondido en las inmediaciones de la casa y a través de un tubo dirigía el gas letal hasta la misma. Las primeras pesquisas permiten a los agentes deducir que el crimen ha sido llevado a cabo por una única persona, pero, ¿quién? A lo largo del invierno varias personas habían visitado a la fallecida, concretamente 8. Estas son consideradas desde un primer momento sospechosas. Debido a la intensa nieve todos los visitantes habían accedido al pueblo desde el único acceso posible, la estación de tren de Canfranc. El guardia de seguridad de la estación recuerda haber visto a los 8 sospechosos exactamente en dos ocasiones, una cuando venían y otra cuando se iban, lo que confirma que cada sospechoso visitó a la víctima una única vez. Sin embargo, el guardia no recuerda las fechas exactas de paso de cada uno de ellos. La lista de los sospechosos es la siguiente: Laura Díaz (escritora de libros infantiles), Inés Mármol (cantante de un grupo punk), Javier Fernández (cómico/guionista), Ramón Nogueras (activista climático), Daniel Pellicer (jugador profesional de golf), Pablo Tristán (cocinero de renombre), Alejandro Sánchez (violinista) y Maja Wrzeistein (profesora de literatura hispánica). En los interrogatorios, los sospechosos no saben precisar las fechas exactas en las que estuvieron en la casa de la fallecida, pero sí son capaces de describir claramente a los agentes con quienes coincidieron: - Laura dice haber coincidido con Javier y con Maja. - Inés aseguró haber visto a Ramón, Pablo y Daniel. - Javier recuerda haber visto a Laura, Alejandro, Daniel y Ramón. - Ramón comenta haber visto a Inés y a Javier. - Daniel recuerda haber visto a mucha gente, concretamente a Javier, Alejandro, Pablo e Inés. - Alejandro aseguró haber coincidido con Javier, Daniel, Pablo y Maja. - Pablo dice haber visto sólo a Inés, Alejandro y Daniel. - Maja comenta haber visto sólo a Laura y a Alejandro. Los inspectores observan que las versiones de los sospechosos no presentan contradicciones y en principio no parece que nadie esté mintiendo, ¿o quizá sí? En esta nueva entrada del ABCdario de las matemáticas se reta al lector intrépido a resolver este crimen utilizando teoría de grafos. ¿Sabría determinar quién es el culpable de este crimen? NOTA: la próxima semana aparecerá explicada con detalle la solución al enigma de la profecía de la Alhambra, y la presente, a la siguiente. De este modo, el lector tiene quince días para meditar tranquilamente sus respuestas. Víctor M. Manero (@pitimanero) es profesor de la Universidad de Zaragoza y miembro de la comisión de divulgación de la Real Sociedad Matemática Española. El ABCDARIO DE LAS MATEMÁTICAS es una sección que surge de la colaboración con la Comisión de Divulgación de la Real Sociedad Matemática Española (RSME) |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |