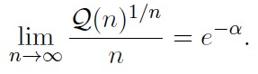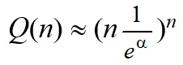¿Ha resuelto un profesor de Harvard el antiguo problema de las damas del ajedrez?
¿Ha resuelto un profesor de Harvard el antiguo problema de las damas del ajedrez? |
 |
 |
 |
|
ABC, 7 de Febrero de 2022
La noticia de la resolución de un enigma de hace 150 años ha corrido como la pólvora, pero las cosas no son tan sencillas
Una de las soluciones al problema de las ocho damas - Archivo
Hace unos días se difundió en las agencias de noticias y, posteriormente, en algunos medios de comunicación, la noticia de que un matemático de Harvard había resuelto un problema propuesto hace 150 años. Como todo, hay que hacer algunas matizaciones. En 1848, el ajedrecista Max F. W. Bezzel (1824 – 1871) propuso la cuestión de cómo disponer ocho damas en un tablero estándar de ocho por ocho escaques de manera que ninguna amenazara al resto (la dama se puede desplazar a todas las de su fila, columna o diagonales). Aunque los matemáticos y profesores de matemáticas llevemos la fama de proponer problemas y ejercicios de nuestra asignatura constantemente (tanto que gran parte del tiempo de las clases nos la pasamos resolviéndolos y explicando sus soluciones), hay muchas otras disciplinas en las que se plantean montones de ejercicios. Los juegos son una parcela importante en estos menesteres, en particular el ajedrez. Y miren ustedes por donde, hay una conexión muy estrecha entre ellos y las matemáticas, habida cuenta de que éstas son capaces de modelizar de modo abstracto prácticamente cualquier actividad humana.
Matemáticos y ajedrecistas célebres pensaron en el problema de las ocho damas, y encontraron varias soluciones. Entonces se planteó la cuestión de cuántas maneras diferentes es posible hacerlo. La primera solución completa la describió sólo dos años después, en 1850, el matemático Franz Nauck. Y a su vez planteó el problema general de las n damas: dado un tablero cualquiera de n x n escaques, ¿de cuántas maneras diferentes se pueden disponer n damas, sin que ninguna amenace al resto? Por cierto, una cuestión previa, mucho más sencilla de resolver: ¿podrían situarse más de n damas verificando esa condición? La respuesta es obviamente negativa, como máximo pueden ser n damas, porque no puede haber más de una por fila y/o columna. Ahora bien, ¿se pueden controlar todas las casillas del tablero con menos de n damas para un tablero n x n? ¿Cuál sería el número mínimo, y donde deberían colocarse? ¿Y cuántas configuraciones diferentes habría? Para nuestro problema inicial, en un tablero 8 x 8, hay 92 soluciones (en la imagen anterior vemos una posible), aunque sólo 12 de ellas son esencialmente distintas, ya que las restantes se deducen de esa docena por giros y simetrías. Pero antes de abordar esta situación, examinemos casos con menos casillas, para comprender mejor el problema. Tablero 4 x 4Analicemos el problema en sus primeros casos. Si el tablero fuera de una sola casilla (1 x 1), es evidente que hay una sola manera de colocar una dama. En los tableros 2 x 2 y 3 x 3 no es posible situar respectivamente 2 y 3 damas sin que se amenacen mutuamente. Veamos en el caso 4 x 4.
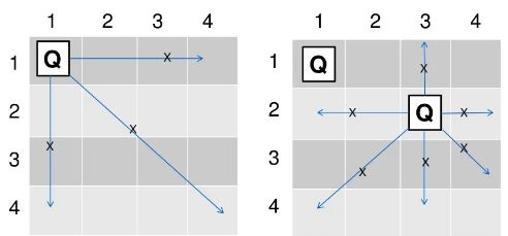
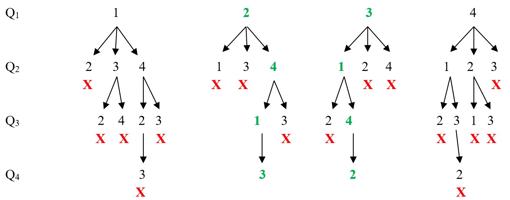
Si colocamos una dama en la primera casilla del tablero 4 x 4 (véase la imagen), teniendo en cuenta las casillas que amenaza (las flechas dibujadas), entonces queda claro que la segunda dama tiene que colocarse en cualquiera de las casillas que no sean esas. Por ejemplo, la podemos colocar en la posición (2, 3) que vemos en el dibujo contiguo. Dibujando de nuevo flechas para ver qué casillas controla, vemos que sólo quedaría la casilla (4, 2) para colocar una tercera dama. Y ya no podríamos poner ninguna más. Por tanto, no existe solución cuando colocamos una dama en la primera casilla del tablero. Para controlar todas las posibilidades ordenadamente podemos establecer un esquema. Utilizaremos un algoritmo conocido como backtracking (vuelta atrás), que suele ser útil cuando tenemos condiciones o restricciones que cumplir, como es el caso. Fue descrito por primera vez por el matemático norteamericano D. H. Lehmer en la década de 1950. Funciona del siguiente modo: comenzamos la búsqueda y en el momento en que llegamos a una contradicción o un valor incorrecto, retrocedemos (de ahí el nombre de 'vuelta atrás') a la elección anterior, y proseguimos desde ahí. En nuestro caso, sabemos que no podemos tener más de una dama por fila. Enumeramos a las cuatro damas que hay que colocar como Q_1, Q_2, Q_3, Q_4, entendiendo que la primera se va a colocar en la primera fila, la segunda en la segunda, y así sucesivamente. Comenzamos viendo las posibilidades que hay en la primera fila, en la que colocamos la primera dama (Q_1) en la primera casilla de la primera fila (posición (1, 1)). Como esa dama controla las casillas de la primera fila y la primera columna, como vemos en la imagen anterior, en ellas no podemos colocar la dama Q_2 que debe ir en la segunda fila. Sólo podemos colocarla en las columnas 2, 3 o 4. Por eso en el gráfico en árbol que vemos a continuación, salen flechas sólo para la segunda fila a las columnas 2, 3 y 4. Ahora bien, como la dama también controla la diagonal, la segunda dama no se puede poner tampoco en la casilla (2, 2). Por eso, bajo el número 2 se ha colocado una cruz de color rojo, porque esa posibilidad no se puede dar. Volvemos entonces atrás, a la columna 3 de la segunda fila, y allí colocamos la segunda dama, Q_2. Como antes, esa dama controla su fila y su columna, por lo que bajo el 3 no puede haber otro 3. Nos quedan entonces como posibilidades solamente las columnas 2 y 4 (recordemos que la 1 quedaba descartada por haber colocado allí la primera dama, Q_1). ¿Podríamos colocar la tercera dama Q_3 en las columnas 2 o 4? Viendo las casillas en diagonal que controla Q_2, vemos que ninguno de los dos casos es posible. Por eso, bajo el 2 y el 4 de la tercera fila aparecen las consiguientes cruces rojas, porque por ahí no se puede continuar. Volvemos entonces atrás, y consideramos la posibilidad de colocar Q_2 en la columna 4 en lugar de en la 3. Y vamos razonando del mismo modo en cada caso. Comprobamos así que no es posible colocar las cuatro damas en el tablero 4 x 4 cuando ponemos la primera en la posición (1, 1). La siguiente posibilidad sería colocar la primera dama Q_1 en la posición (1, 2), es decir, primera fila, segunda columna. Como antes, bajo el 2 del esquema sólo podremos situar la segunda dama en las columnas 1, 3 y 4 (a las que vemos que van las flechas). Sin embargo, ni en la columna 1 ni en la 3 de la segunda fila podríamos colocar la segunda dama, porque esas diagonales las controla Q_1. Por eso, bajo los números 1 y 3 aparecen sendas cruces rojas. No quedaría más remedio que colocarla entonces en la columna 4. Y así vamos razonando con cada caso. El esquema muestra todas las posibilidades, habiéndose marcado en color verde, las únicas dos posibilidades de solución del problema.
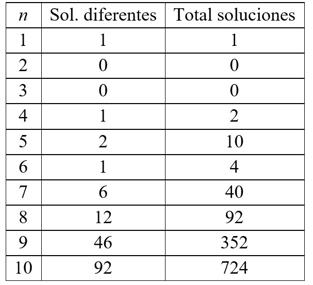
Esas dos soluciones podemos describirlas en una sola línea como 2413 y 3142. Serían las que aparecen en los siguientes cuadros, respectivamente. Tras confirmar que, en efecto, son las posiciones de 4 damas en un tablero 4 x 4 sin que ninguna amenace a las demás, observamos que tienen algo en común: son simétricas respecto a un imaginario eje vertical central (también respecto a uno horizontal). Por eso, para los matemáticos, en realidad es una única solución, porque una se puede deducir de la otra por simetría. En este tipo de ejercicios suele decirse 'tantas soluciones', añadiendo la coletilla 'salvo giros o simetrías'. Obsérvese que la simetría puede detectarse también en la forma descrita numéricamente: 3142 es 2413 escrito del final al principio. Si tienen ánimo pueden tratar de deducir con razonamientos análogos al de 4 x 4, cómo serían las soluciones de los casos 5 x 5, 6 x 6, etc. En el siguiente cuadro se recogen las posibilidades que existen hasta orden 10:
Tablero 8 x 8Como indicamos anteriormente, el problema original de las 8 damas fue resuelto a los dos años de su planteamiento. En el libro 'Ajedrez y Matemáticas' (Ed. Martínez Roca, 1974) aparecen descritas las 12 soluciones diferentes al mismo. Con la notación expuesta anteriormente serían 1) 15863724 2) 16837425 3) 24683175 4) 25713864 5) 25741863 6) 26174835 7) 26831475 8) 27368514 9) 27581463 10) 35281746 11) 35841726 12) 36258174 Todas ellas tienen 7 simetrías diferentes (aparte de la descrita), salvo la décima que sólo tiene 4 (la dada y las de giros de 90º, 180º y 270º del tablero). Una sencilla cuenta nos da por tanto todas las soluciones posibles: 11 x 8 + 4 = 92. Un número pequeño si tenemos en cuenta que ocho damas pueden colocarse en 61 escaques, ¿de cuántas formas? (Repasen la Combinatoria: serían combinaciones de 64 elementos tomados de 8 en 8, es decir, 4.426.165.368 solamente). En la primera imagen de este artículo aparece la solución 47382516. Es una situación simétrica de las 12 dadas anteriormente. ¿Saben de cuál de ellas? Tablero n x nConforme aumenta el número de filas y columnas del tablero, el número de soluciones crece considerablemente. En el caso de un tablero 20 x 20, por ejemplo, el número de soluciones diferentes es de 4.878.666.808 y el total, contando todas sus simetrías y giros de 39.029.188.884. Todas ellas se han calculado con algoritmos y ordenadores. Pero no existe una expresión general que nos diga ésta o aquella es esa cantidad.
El becario postdoctoral Michael Simkin, del Centro de Ciencias y Aplicaciones Matemáticas de la Universidad de Harvard (Cambridge, Massachusetts, EE. UU.) y Zur Luria, graduado de la Universidad hebrea de Jerusalén y experto ajedrecista, han estado cinco años trabajando en el problema, con varios artículos publicados. Hace unas semanas Simkin ha publicado un nuevo artículo en solitario en el que recapitula todas sus investigaciones y explica con cierto detalle los algoritmos desarrollados en sus trabajos. Los medios de comunicación se han hecho eco de la noticia recalcando, como siempre, lo espectacular: que si es un problema planteado hace 150 años, que si ha logrado dar una cota inferior al valor exacto, es decir, una aproximación al número mínimo de configuraciones posibles, y es la cifra más cercana que se puede obtener en este momento todas estas configuraciones distintas para un tablero n x n:
Y más. Si el lector calcula los valores que esa expresión desde n igual a 1 en adelante, y los compara con los valores exactos que hemos descrito en la tabla descrita más arriba, realmente no parecen aproximaciones demasiado 'buenas': [0.143, 0.0817, 0.0789, 0.10704, 0.1868, 0.3989, 1.007, 2.9336, 9.68739, 35.7569] y probablemente exclame: «¡¡Cinco años para esto!!». Cuando un matemático lee ese tipo de noticias, con valores numéricos como ese 0.143, lo primero que hace es preguntarse «¿de dónde sale?». Y acaba yendo a la fuente original, al artículo. Y descubre que las cosas no son tan simples como han difundido los medios de comunicación. Para empezar, con un vistazo rápido, el artículo (de 51 páginas) contiene un montón de resultados, proposiciones y demostraciones nada triviales, y además ese 0.143 no aparece por ninguna parte. Bueno, aparece, pero no así. El objeto del artículo es demostrar que, si Q(n) son el total de posibles configuraciones en que una dama puede colocarse en un damero n x n sin que ninguna esté amenazando a ninguna de las demás, entonces existe una constante α que se encuentra en el intervalo (1.94, 1.9449) tal que:
Es decir que, asintóticamente (a grandes rasgos, que los valores son más precisos cuanto más grande es n; por eso los valores de n pequeños resultan muy malos), el número de configuraciones se 'acerca' a esa cota inferior. Por cierto:
de ahí el 0.143 de la fórmula. Del límite anterior, para n lo suficientemente grande (detalle que se obvia y es muy importante para entender lo que se ha obtenido):
lo cual 'acerca' el resultado del paper con lo publicado en los medios de comunicación. En dicho artículo Simkin ha utilizado algoritmos de tipo probabilístico y combinatorio: esencialmente algoritmos voraces aleatorios y de absorción. Su mecanismo no es difícil de comprender; en posteriores entregas podemos explicar brevemente en qué consisten a grandes rasgos, con ejemplos entendibles. Mediante otros algoritmos (concretamente uno de tipo entropía), el autor ha determinado también un límite superior al número de posibles configuraciones, es decir, el mayor número posible de ellas, de modo que tenemos acotado el valor exacto entre dos aproximaciones, que no distan mucho entre sí, para cualquier valor de n, por grande que sea. Pero de nuevo, con el matiz que hemos comentado para interpretar esas cotas.
Alfonso J. Población Sáez es profesor de la Universidad de Valladolid y miembro de la Comisión de divulgación de la RSME. El ABCDARIO DE LAS MATEMÁTICAS es una sección que surge de la colaboración con la Comisión de Divulgación de la Real Sociedad Matemática Española (RSME) |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |