¿Qué son los métodos Montecarlo y qué tienen que ver con la bomba atómica?
¿Qué son los métodos Montecarlo y qué tienen que ver con la bomba atómica? |
 |
 |
 |
|
ABC, 9 de Mayo de 2022
La idea, relacionada con la generación de números aleatorios, surgió cuando el matemático polaco Stanislaw Ulam resolvió un complicado solitario
El próximo viernes 13 de mayo se cumplen treinta y tantos años del fallecimiento del matemático polaco Stanislaw Ulam (1909 – 1984), uno de los integrantes del proyecto Manhattan, que como sabrán, se encargó entre otras cosas de conformar la primera bomba de hidrógeno de la Historia. Desgraciadamente nos hallamos en un periodo en el que vuelven a aparecer nítidamente los dilemas morales sobre la utilización de la energía nuclear con fines no precisamente pacíficos. Ulam fue uno de los más reticentes y atormentados con el desarrollo final de la bomba atómica. Dejando a un lado esa controversia, claramente no superada, se encuentra la cuestión de qué papel pudo desempeñar un inofensivo matemático (a priori), con sus cálculos y ecuaciones, en un asunto como éste.
Echémosle un vistazo. Si buscamos información sobre Ulam, encontraremos que sus contribuciones matemáticas se distribuyen en campos tan diferentes como la teoría de números, la teoría de conjuntos, la teoría ergódica y la topología algebraica. Evidentemente no podemos repasar tanto material en una única reseña, de modo que nos centraremos en esta ocasión en el modelo que desarrolló junto con otro genio de las matemáticas y la informática, que también trabajó en el Laboratorio de Los Álamos en el citado proyecto Manhattan, el matemático húngaro-estadounidense John Von Neumann (1903 – 1957), el conocido como método de Montecarlo. Antes de nada conviene recordar algunas ideas que nos aclaren un poco el tipo de problemas con los que vamos a tratar. A la hora de modelizar cualquier fenómeno o circunstancia que sucede a nuestro alrededor (experimento que puede ser tan sencillo como lanzar al aire una moneda, o tan complejo como describir la evolución del agua cuando se rompe una tuberia dentro de un edificio; o cómo simular el movimiento de difusión de neutrones en el material de fisión nuclear). Esa modelización de lo que puede ocurrir se realiza mediante un algoritmo (palabreja que se ha hecho familiar en nuestras vidas desde hace algún tiempo). Un algoritmo no es ni más ni menos que unas reglas fijas, siempre las mismas, que reproducen un proceso. Por ejemplo, para sumar, restar, multiplicar o dividir dos números utilizamos en cada caso un algoritmo (los que nos han enseñado en la escuela), la elaboración de una tarta, el desplazamiento de los autobuses por una ciudad, la interpretación de una canción, todo lo que hacemos (a veces con algunas variaciones, en cuyo caso, modificamos el algoritmo) puese describirse mediante unas reglas, mediante un algoritmo. Los experimentos (que modelizamos mediante esos algoritmos) pueden clasificarse en dos tipos básicos: deterministas y aleatorios (o probabilisticos). Es determinista cuando su resultado es idéntico siempre que partamos de las mismas condiciones (si dejamos caer un objeto, sabemos con toda seguridad que acaba en el suelo; si calentamos una olla con agua, sabemos que acabará hirviendo), mientras que es aleatorio cuando no tenemos garantizado el mismo resultado aunque hagamos lo mismo (tirar al aire una moneda, extraer una bola de una urna, saber dónde va a caer un rayo). En realidad sólo los fenómenos naturales son puramente aleatorios, porque lo de la moneda, la bola de la urna, etc., podríamos intuir su comportamiento estudiando dicha moneda, o la máquina que extrae la bola. Por eso hablamos de experimentos seudoaleatorios (los que dependen de algún artefacto construido por el hombre) y puramente aleatorios. Pero no haremos tal distinción en lo que sigue, por simplificar las cosas. La modelización de los experimentos o fenómenos deterministas se fundamenta en una fórmula conocida y cerrada, mientras que los segundos se basan en la generación de números aleatorios y el análisis de las probabilidades asociadas. Juegos de cartasEn el trabajo que realizaban sobre la difusión de partículas en la fisión nuclear, los físicos que integraban el proyecto Manhattan se percataron de que ésta poseía un comportamiento completamente aleatorio. Para su estudio podían optarse por dos procedimientos: resolver las ecuaciones íntegro-diferenciales que gobiernan la dispersión, la absorción y la fisión, o tomar datos a partir de experimentos reales. Ni una ni la otra eran factibles (la primera porque no se saben resolver ese tipo de ecuaciones en modo exacto; la segunda porque evidentemente no podemos hacer desintegraciones atómicas). Stan Ulam era un apasionado de los juegos de cartas y el cálculo de probabilidades para encontrar métodos trucos para tratar de tener ventaja sobre el rival. Precisamente, jugando un solitario, se percató de que resultaba más simple tener una idea del resultado general del solitario haciendo pruebas múltiples con las cartas y contando las proporciones de los resultados, que computar todas las posibilidades de combinación formalmente. Esas pruebas múltiples las podía hacer generando números aleatorios con el ordenador y viendo los resultados. Por supuesto, una persona puede hacerlo varias veces, pero un ordenador puede pasarse horas generando números, y en ese tiempo hacer cientos, miles, millones hoy en día, de simulaciones. Entonces se dio cuenta de que lo mismo podía aplicarse para inferir el comportamiento de un fenómeno físico, como el de la difusión de neutrones. Ulam explicó la idea a Von Neumann. Aunque inicialmente no le convencía, con el tiempo (y es de suponer alguna experimentación) se convirtió en un auténtico fan convencido del procedimiento. Como todo lo que hacían en Los Álamos era secreto, dieron al proyecto un nombre en clave, que uno de los integrantes del grupo bautizó como Montecarlo, en referencia al célebre Casino de esa localidad. Al fin y al cabo lo que genera la ruleta son números aleatorios (como comenté antes falso, porque al depender de un mecanismo mecánico, es seudoaleatorio; de hecho muchos jugadores han tenido grandes beneficios observando el comportamiento de las ruletas y deduciendo una fórmula empírica que las modelice), aunque al parecer Ulam aceptó el nombre en “honor” a un tío suyo que no hacía más que pedir dinero prestado a todo el mundo para jugar allí. Fuera como fuese el caso es que los métodos Montecarlo fueron fundamentales para las simulaciones requeridas, aunque bastante limitados por las herramientas informáticas de aquella época (una ENIAC). En 1948 lograron los primeros resultados aceptables sobre el comportamiento de un núcleo de fisión. En la década de 1950, los métodos Montecarlo fueron decisivos para el desarrollo de la bomba de hidrógeno y se popularizaron en los campos de la física, la química física y la investigación operativa. La Rand Corporation y la Fuerza Aérea de los EE. UU. fueron dos de las principales organizaciones responsables de financiar y difundir información sobre estos métodos. Desde entonces no han parado de perfeccionarse y encontrarse aplicaciones en los campos más variopintos, entre los que destacan la física, la medicina (imágenes radiográficas, sobre todo), la química molecular, ingeniería, diseño gráfico, economía y negocios y, por supuesto, las matemáticas. Ejemplos
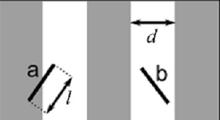
Suele mencionarse el experimento de la aguja de Buffon para estimar los decimales del número Pi como precursor de los métodos Montecarlo. Si tomamos una hoja de papel en la que marcamos unas líneas paralelas a distancia d entre ellas (ver imagen), y dejamos caer una aguja de longitud l < d sobre el papel, pueden darse dos situaciones: que la aguja quede entre dos de las líneas (situación b de la imagen), o que caiga entre dos de las franjas, cortando a una de las líneas (situación a). La probabilidad p de que la aguja esté en la posición a es
Más adelante, Pierre Simon de Laplace (1749 – 1827) interpretó esa relación como un modo de encontrar aproximaciones a los decimales de Pi. ¿Cómo? Tirando la aguja muchas veces y contando el número de las que quedaban en la situación a. Ese valor dividido por el número total de lanzamientos, se aproxima a ese valor de la probabilidad p, y por tanto facilita también el cálculo de Pi:
Por supuesto, la aproximación obtenida es muy poco eficiente: lograr así 5 decimales correctos con 3400 lanzamientos está por debajo del 1.5%. Simplemente trata de plasmar la idea de los métodos Montecarlo: cuantos más lanzamientos, más nos aproximamos. Cuando jugamos a los barcos, al principio, hasta “definir” las zonas por donde se halla el objetivo, también utilizamos una estrategia Montecarlo: “lanzamos” andanadas al azar, y cuantas más, mejor queda definida la zona donde se encuentran los barcos del oponente. Un procedimiento similar utilizan los guardacostas para localizar las probables ubicaciones de personas o buques en los naufragios (véase el software SAROPS, por ejemplo) durante las operaciones de búsqueda y rescate. Cada simulación puede generar hasta diez mil puntos de datos que se distribuyen aleatoriamente en función de las variables proporcionadas. Los patrones de búsqueda luego se refinan en base al análisis de estos datos para optimizar la probabilidad de contención y la probabilidad de detección, que en conjunto equivalen a una probabilidad general de éxito. En última instancia, esto sirve como una aplicación práctica de la distribución de probabilidad para proporcionar el método de rescate más rápido y conveniente, que se ha probado eficaz en el salvamento de vidas y la optimización de recursos. En matemáticas, hay muchos lugares en los que se emplean estos métodos, desde la aproximación de integrales o la estimación de soluciones de ecuaciones que no se saben resolver en modo exacto, hasta la determinación de si un número de cientos de dígitos es o no primo (test de primalidad). Aventuras de un matemáticoHace pocos meses, se estrenó la película 'Adventures of a Mathematician' (Thor Klein, Alemania, Polonia y Reino Unido, 2020) sobre Stanislaw Ulam y su trabajo junto a otros científicos en Los Álamos. Mejor dicho, se estrenó en más de una docena de países, entre los que no está el nuestro. De acuerdo que no es una película de acción trepidante, ni de superheroes, ni es una comedia (de hecho deja bastante mal cuerpo, ya que nos explica cómo asesinaron a la familia de Ulam en el Holocausto, y los problemas de conciencia que constatemente surgían en el grupo de trabajo de la bomba atómica y la posterior de hidrógeno, aspectos sobre los que deberían reflexionar algunos dirigentes en la actualidad antes de hablar tan alegremente de las armas nucleares; paradojicamente, en Rusia sí se ha estrenado). La película se basa en el libro homónimo de Ulam, editado en 1984, que tampoco se ha publicado en español (los temas científicos parece que se nos atragantan, junto a los idiomas, así que en este caso, lo tiene todo). No obstante, se lo recomiendo si tienen ocasion de hacerse con él. Sobre la película, aquí disponen del trailer. En la imagen una escena en la que Ulam enseña algunos trucos sobre juegos de cartas a sus alumnos en base al cálculo de probabilidades. Volveremos sin duda a recordar otros trabajos de Ulam en posteriores reseñas, como una espiral de la que seguro han oído hablar.
Alfonso J. Población Sáez es profesor de la Universidad de Valladolid y miembro de la Comisión de divulgación de la RSME. El ABCDARIO DE LAS MATEMÁTICAS es una sección que surge de la colaboración con la Comisión de Divulgación de la Real Sociedad Matemática Española (RSME) |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |