La Cosmología pitagórica

La veneración hacia el número diez tiene para los pitagóricos una implicación cosmológica transcendental en su doctrina acerca de la configuración del universo, al ser la inspiradora del primer sistema astronómico no geocéntrico. Según Aristóteles (Metafísica, 986a):

«[...] Como creen [los pitagóricos] que la década es perfecta y que abarca la naturaleza entera de los números, afirman que también los cuerpos que se mueven en torno de los cielos son diez, pero al ser nueve solamente los visibles, se inventan, por esta razón, el décimo, la anti-tierra, [...].»

Aristóteles desarrolla estas ideas más ampliamente en su obra Del Cielo (293a):

«La mayoría de los pueblos dicen que la tierra está situada en el centro del universo, [...], pero los filósofos pitagóricos sostienen lo contrario. Dicen que en el centro está el fuego y que la tierra es uno de los astros que, al moverse circularmente en torno al centro, da lugar al día y a la noche, [...].»

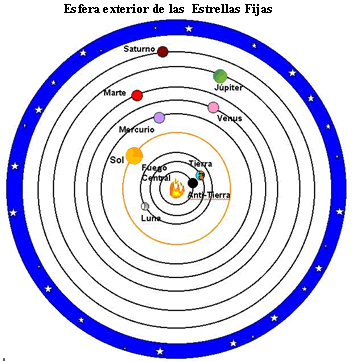
Ocho cuerpos celestes: la tierra, la luna, el sol y los cinco planetas conocidos (Mercurio, Venus, Marte, Júpiter y Saturno), giran en órbitas circulares concéntricas en torno al fuego central –«Trono de Zeus»–, situado en el centro del universo. Con la Esfera de las estrellas fijas se llega al valor nueve. Como falta uno para alcanzar el valor diez de la Tetractys, emblema sagrado de los pitagóricos, se añade al sistema –«de modo que toda su teoría fuera coherente»–, como dice Aristóteles, la antitierra, situada en la órbita más interior, en equilibrio con la tierra, alineada con ésta y con el fuego central y con el mismo período de revolución diaria que ella. El sol no era el centro del universo, ni era el creador de su propio calor, sino que era una especie de cristal reflector que recogía la luz y el calor del fuego central, en torno al cual giraba con un período de un año. Las estrellas fijas permanecían estacionarias, mientras que la tierra mantenía, durante su movimiento, el mismo hemisferio deshabitado hacia el fuego central de modo que sus habitantes no podían ver jamás ni el fuego central ni la anti-tierra.

Al desplazar a la tierra del centro del universo, la cosmología pitagórica supone un heroico salto de imaginación científica. No se trata de una mera fantasía arbitraria. De hecho el sistema proporcionaba una explicación plausible de los eclipses. No es exactamente una anticipación de la teoría heliocéntrica, pero algunos estudiosos de la Historia de la Cosmología lo consideran de rango superior en importancia a la identificación del fuego central con el sol.

La teoría pitagórica es de una gran originalidad. Para Tales y otros filósofos presocráticos como Anaxímenes, Heráclito, Parménides y Empédocles la tierra estaba ciertamente en reposo en el centro del universo esférico y más tarde Eudoxo y por supuesto Aristóteles volvieron a situar con firmeza la tierra en el centro, del que no se movería hasta los primeros balbuceos heliocéntricos de Aristarco. Para pensadores como G. Bruno el giro copernicano no sería una novedad sino la restauración de la antigua Cosmología pitagórica. Así pues, como en otros muchos aspectos del pensamiento pitagórico, carácter místico y religioso, no le resta valor científico.

Clasificación y denominación pitagóricas de los números

Según Isidoro de Sevilla (Etimologías, III.2): «Pitágoras fue el primero que escribió sobre la ciencia del número», es decir, a Pitágoras se debe la primera depuración filosófica o teórica de la Aritmética –la liberación de la Ciencia del Número de la práctica de artesanos y mercaderes que constituían la llamada Logística–. Sobre ello escribe Aristóxeno:

«Pitágoras honró a laAritmética más que ningún otro. Hizo grandes avances en ella, sacándola de los cálculos prácticos de los comerciantes y tratando todas las cosas como números».

Los pitagóricos realizaron diversas clasificaciones y acuñaron numerosos nombres para los diversos tipos de números. Pero debido a su proceder místico, muchas de sus definiciones son bastante abstrusas de forma que conviene a veces recurrir a los preliminares del Libro VII de Los Elementos de Euclides, donde se recogen gran parte de ellas, en el lenguaje inteligible y riguroso característico del gran compilador de la Matemática griega elemental. Veamos los nombres y definiciones de algunos números:

• Parmente par: cuando su mitad es par (son de la forma 2^n·[2k+1], n>1).
• Imparmente par: cuando su mitad es impar (son de la forma 2·[2k+1], n>1).
• Parmente impar: cuando al ser dividido por un número impar da uno par (son de la forma 2^n·[2k+1]·p, n>1).
• Imparmente impar: cuando no tiene más que divisores impares.

«Es divisor de» (Euclides D.VII.3). «Es múltiplo de» (Euclides D.VII.5).

Números primos (Euclides D.VII.11) y compuestos (Euclides D.VII.13).

Números lineales, planos y sólidos:

• Lineal: es el que no tienen divisores (es decir, los primos).
• Plano: es el producto de dos números que son sus lados (Euclides, D.VII.16).
• Sólido: es el producto de tres números que son sus lados (Euclides, D.VII.17).
• Cuadrado: es el producto de un número por sí mismo (Euclides, D.VII.18).
• Cúbico: es el producto de un número por sí mismo dos veces (Euclides, D.VII.19).

Números perfectos, deficientes y abundantes. Números amigos.

• Deficiente: es un número que es menor que la suma de sus partes alícuotas.
• Abundante: es un número que es mayor que la suma de sus partes alícuotas.
• Perfecto: es un número que es igual que la suma de sus partes alícuotas.
• Números amigos: son números en los cuales cada uno es igual a la suma de los divisores del otro.

Los números perfectos y los números amigos han causado siempre una gran fascinación, por eso la búsqueda de números perfectos y amigos ha desplegado un derroche de tinta matemática desde los primeros tiempos pitagóricos hasta nuestros días, en los que se aplican potentes instrumentos de computación. Los primeros pitagóricos sólo conocían los números perfectos 6 y 8. Euclides define el número perfecto en D.VII.22.

A los números amigos, literalmente habría que llamarlos números enamorados. Los pitagóricos sólo conocieron el par 220, 284:

284 = 1+2+4+5+10+11+20+22+44+55+110(suma de los divisores de 220),

220 = 1+2+4+71+142(suma de los divisores de 284) .

Jámblico atribuye el descubrimiento de los números amigos al propio Pitágoras, embelleciendo el relato del mismo con la siguiente anécdota: «Siendo preguntado Pitágoras –¿qué es un amigo?, contestó –Alter ego. Por analogía aplicó el término amigos a dos números cuya suma de partes alícuotas es igual al otro».

La Música pitagórica y la Teoría de las medias

Según Nicómaco, Gaudencio, Porfirio, Diógenes Laercio, Teón de Esmirna, Jámblico, Boecio y otros pitagóricos, Pitágoras estudió, quizá por primera vez en la historia, las primeras leyes cuantitativas de la Acústica, al determinar el fundamento matemático de la armonía musical con la realización de la primera experiencia científica que consigna la historia, mediante la construcción de un instrumento, el monocordio (Jámblico, XXXVI.119; Diógenes Laercio, VIII.12),con el propósito de interrogar a la naturaleza y obligarla a responder a una cuestión concreta: ¿cuál es la relación precisa, si es que existe, entre la armonía musical y los números? Pitágoras descubre que las cuerdas que daban el tono, la cuarta, la quinta y la octava, tenían longitudes proporcionales a 12, 9, 8 y 6. Y puesto que las razones entre los números 12, 9, 8 y 6 son iguales a las que hay entre 1, 3/4, 2/3 y 1/2, que son las más sencillas que se pueden formar con los números de la sagrada Tetractys, 1, 2, 3 y 4, Pitágoras dedujo que ésta es «la fuente y raíz de la Naturaleza eterna» como dicen los Versos Dorados. Como en tantos aspectos pitagóricos los números de la Tetractys eran la piedra angular de la armonía musical. Mediante una mística extrapolación, la Tetractys sería la fuente del conocimiento de las raíces de la armonía del Cosmos divino, alcanzable a través del número.Si en el número está la clave del tono musical, en él residirá también la clave de toda la naturaleza y en ultima instancia aparecía la matriz de la filosofía pitagórica: «el número es la esencia de todas las cosas». Con este feliz descubrimiento Pitágoras instaura algo nuevo en la Historia del Pensamiento: el método experimental y la expresión en fórmulas matemáticas de las leyes de la naturaleza.

La teoría musical de Pitágoras tiene que ver también con la Teoría de las medias de raíz pitagórica. Así lo señala el pitagórico Arquitas: «En música hay tres medias: la media aritmética, la media geométrica y la subcontraria, llamada también armónica».

Dados dos números a y b, se definen las medias aritmética, m, armónica, h, y geométrica, g, de la forma: , verificándose que : Estas relaciones son verificadas por las proporciones musicales que se derivan de la cuaterna de números 12, 9, 8, 6 del experimento pitagórico sobre el monocordio: 

El fundamento matemático de la armonía musical se representa en la tablilla sostenida por un joven discípulo de Pitágoras. En la parte superior de las cuerdas de la lira aparecen con tipografía romana los números 6, 8, 9, 12, de las proporciones musicales. Las consonancias musicales se denominan de forma literal y numérica: diatéssaron (6/8, 9/12); diapente (6/9 y 8/12); diapasón u octava (6/12). Además, en la parte inferior del diagrama de Rafael aparece el número 10 bajo la forma de la sagrada Tetractys como emblema pitagórico que resume las razones musicales.