• Estudiar la figura.
• Trazar a lápiz las líneas necesarias para dividirla en las partes que se piden.
• Comprobar, midiendo, recortando si es necesario o razonando si las partes obtenidas son iguales.

Todo esto exige y potencia en nuestros alumnos capacidades importantísimas en su desarrollo personal e intelectual, que todas las áreas del currículo deberían tener en sus objetivos generales, como son:

1. Atención y observación. Hay que dedicar un tiempo a analizar la figura, ver los segmentos que la determinan y los ángulos que producen.
2. Discriminación. Separar claramente los trozos iguales que queremos obtener.
3. Percepción visual. Dice Lev Vigotsky, pedagogo ruso (1896-1934): “El proceso entero de la resolución de un problema está básicamente determinado por la percepción”. Esta frase expresa la importancia de la estimulación perceptiva para el conjunto de los aprendizajes, y por ello hay que trabajar aspectos importantes de la percepción visual, como la coordinación vasomotora, la discriminación figura-fondo, la constancia de forma, las posiciones en el espacio y las relaciones espaciales.
   En general, "vemos lo que sabemos ver”, y esto implica operaciones complejas como son: la selección (que aísla lo que interesa dejando todo el resto como 'fondo'); la clasificación (que ordena, jerarquiza y categoriza); la evaluación (que asigna valor y pondera para actuar); el simbolismo (que significa y abstrae) y la autoconsciencia del entorno.
4. Imaginación y creatividad. Representar mentalmente las posibles divisiones antes de utilizar el lápiz y la regla.
5. Paciencia y constancia. No rendirse abandonando el problema ante la primera dificultad. Estas cualidades no están trabajadas en muchos de nuestros alumnos y rápidamente surgen comentarios como: “Maestro, esto no me sale”, “No lo veo, maestro”, “Es muy difícil”...

Para evitar estos comentarios, a lo largo del desarrollo de la actividad, hemos de ir dando a los alumnos estrategias de resolución:

• Medir los segmentos que forman el perímetro de la figura.
• Cuadricular o triangular la figura, pues permite conocer la superficie que ha de tener cada uno de los trozos buscados y descartar, por tanto, cortes que no lo cumplan.
• Contar los cuadrados o triángulos y repartirlos.
• Girar la hoja, para ver la figura desde otro punto de referencia.
• Buscar su eje de simetría.

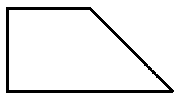
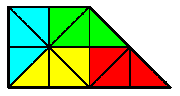
Un ejemplo de triangulación para dividir en cuatro partes iguales se da en el siguiente trapecio rectángulo.

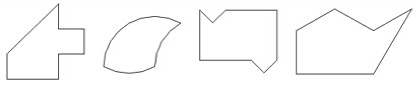
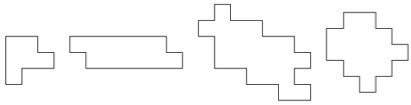
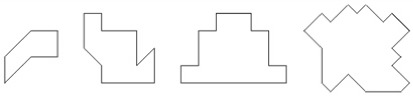
DESARROLLO DE LA ACTIVIDAD

El trabajo a realizar lo podemos dividir en tres niveles de dificultad, y cada uno de ellos con dos apartados a desarrollar:

Nivel 1: Dividir las figuras en dos partes exactamente iguales en forma y tamaño.

Nivel 2: Dividir las figuras en tres partes exactamente iguales en forma y tamaño.

Nivel 3: Dividir las figuras en cuatro partes exactamente iguales en forma y tamaño.

Actividad a. Dada una hoja con dibujos de figuras dividirlas mediante el trazado de líneas rectas, quebradas o curvas en dos (tres o cuatro) partes exactamente iguales en forma y tamaño. Trazar las líneas con regla y bolígrafo, y colorear una de las partes obtenidas.

Actividad b. Diseñar y dibujar en una hoja con trama cuadrada figuras que puedan ser divididas en dos (tres o cuatro) partes exactamente iguales en forma y tamaño.

Ejemplo de actividad 1a.

Ejemplo de actividad 2a.

Ejemplo de actividad 3a.

Las actividades “b” pueden ser intercambiadas entre los alumnos, para así aumentar el banco de figuras disponibles y evaluar el nivel de dificultad de las piezas diseñadas por los compañeros.

PARA FINALIZAR

Una variante de estas actividades consiste en pedir que las partes que se obtengan sean semejantes a la figura original. Esto sólo es posible en algunas figuras y aunque parezca añadir una dificultad mayor, no suele ser así, pues la semejanza conserva los ángulos y esto facilita la localización de los trozos. Como ejemplo sirve el del trapecio rectángulo visto anteriormente.

Estas actividades de dividir en partes iguales, que son verdaderos problemas, son frecuentes en las competiciones y olimpiadas matemáticas que se celebran a lo largo de la geografía española. Profundizando en el enunciado pueden convertirse en pequeñas investigaciones que proponer a los alumnos de nivel más avanzado. Como ejemplo proponemos dos problemas propuestos para la 1ª fase de la XIII Olimpiada Matemática Provincial de Albacete (2002), el primero para 12/14 años y el segundo para 14/16.

Partes iguales.
Dividir un cuadrado en tres, cuatro, cinco... partes iguales. ¿Para qué casos existe más de una solución? Si en lugar de dividir el cuadrado en partes iguales tan sólo se requiere que las partes sean equivalentes, ¿existen otras soluciones?

Dividir triángulos.
a) ¿Es posible dividir un triángulo equilátero en 4 triángulos equiláteros?
b) ¿Es posible dividir un triángulo equilátero en 5 triángulos equiláteros?
c) Demostrar que cualquier triángulo equilátero se puede dividir en n triángulos equiláteros, para cualquier n>5.

Material necesario:

• Regla, lápiz, goma, bolígrafo negro y lápices de colores.
• Hojas con las figuras dibujadas.