Enero 2007: Rompecabezas Africano (publicado en la revista SUMA, número 47, 2004)
Enero 2007: Rompecabezas Africano (publicado en la revista SUMA, número 47, 2004) |
 |
 |
 |
| Escrito por Grupo Alquerque | ||||||||||||||||||
| Lunes 01 de Enero de 2007 | ||||||||||||||||||
|
Aspectos lúdicos de la Topología. Cuando se nombra la palabra Topología, o no se ha oído nunca o suele pensarse en una parte complicada de la matemática, sólo al alcance de aquellos que hayan profundizado bastante en sus estudios matemáticos. Sin embargo, hay aspectos topológicos elementales a los que podemos acercarnos desde edades muy tempranas.
Dado que la Topología es una geometría (de hecho recibe el nombre de Geometría de la Posición) que no tiene interés en la medida, sino solamente en la forma y en cómo ésta puede variar sin provocar roturas (cortes, ni aparición de agujeros), hay elementos de esta disciplina que aparecen antes que el concepto de medida. Aspectos como dentro o fuera, formas equivalentes, conexiones entre agujeros, caminos dentro de laberintos, etc., se pueden abordar en la infancia. Algunos de los primeros juegos infantiles tienen relación con elementos topológicos. Por ejemplo, es frecuente en los primeros años de aprendizaje jugar con estructuras de madera llenas de agujeros por donde los infantes deben hacer pasar una cuerda que está anudada en un extremo; y en casi todos los niños se produce una gran fascinación por la plastilina y la transformación por deformación de unas figuras en otras. Dado su evidente atractivo lúdico, muchos problemas topológicos aparecen en acertijos, rompecabezas y pasatiempos, siendo excelentes pruebas para cualquier competición divertida que podamos plantear a nuestros alumnos. Además hay problemas clásicos como los puentes de Königsberg, el de los cuatro colores, la sorprendente Cinta de Möbius, la conexión entre casas y distribuidores energéticos, etc. que han fascinado durante décadas a los matemáticos o aficionados. Los profesores José Luís Carlavilla y Gabriel Fernández hicieron una presentación de todos estos aspectos y muchos más de una forma amena y apasionante en un libro de obligada lectura (Carlavilla y Fernández; 1994).Juegos y rompecabezas topológicos. Podemos encontrar multitud de juegos con connotaciones topológicas sin saber que estamos relacionándonos con esa materia. Muchos retos o incluso trucos de magia consisten en deshacer situaciones donde aparecen elementos unidos por cuerdas que a simple vista parecen imposibles (Muñoz; 2003). En general, consideraremos como rompecabezas topológicos aquellos formados por cuerdas, maderas, anillas, bolas, alambres, etc., donde una situación, a simple vista irresoluble, puede resolverse mediante traslación de sus elementos, sin romper, rasgar o modificar la estructura topológica del juego. Un estudio muy sistemático e interesante de los laberintos de alambre y de su implicación en la enseñanza puede encontrarse en el artículo publicado por nuestro compañero y amigo Pablo Flores Martínez en el nº 41 de esta misma revista SUMA (Flores Martínez; 2002). Desde el punto de vista matemático, los juegos topológicos potencian aspectos como la intuición, la visión espacial, el estudio sistemático de posibilidades, la búsqueda de soluciones imaginativas, la esquematización de los problemas y muchos más. Un rompecabezas topológico tiene bastante relación con un problema de matemáticas. No solamente porque con frecuencia al enfrentarnos a ellos nos quedamos bloqueados al no saber cómo comenzar, sino porque existen muchos procedimientos de la resolución de problemas que se aplican para resolver el reto que nos plantea el rompecabezas. Entre otros, podemos citar los siguientes heurísticos:
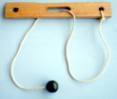
Rompecabezas africano de cuerda. Es, quizás, el puzzle de cuerda más famoso y que podemos encontrar con más facilidad en comercios, internet o incluso como regalo publicitario de algunas empresas. Se considera originario de las tribus guineanas, aunque está bastante extendido. En Estados Unidos se conoce como puzzle del yugo del buey.  Como podemos ver por la imagen, consta de un trozo de madera donde se han realizado tres agujeros por los que se anuda una cuerda que se cruza formando dos lazos. El agujero importante es el central, pues los orificios de los extremos sólo sirven para sujetar la cuerda y que no quede libre (en algunos ejemplares comercializados, la cuerda en sus extremos se incrusta dentro de la madera y sólo tienen el hueco central). En cada lazo aparece una bola, cuya dimensión no le permite pasar por los agujeros de la madera. El objetivo del juego es conseguir colocar las dos bolas en el mismo lazo. Como en todos los rompecabezas de este tipo, es necesario llegar a la solución sin deshacer los nudos que puedan estar a la vista ni romper ninguno de los elementos que forman el juego. La resolución de este rompecabezas es bastante complicada para quien no la conozca, pues existe un cruce de cuerdas a través de los orificios de la madera que no es fácil de imaginar, ni siquiera al manipular el juego. Por ello detallamos los pasos de resolución de este problema.
Una vez presentado el modelo clásico, veamos algunas variaciones, que a simple vista parecen similares, pero cuya resolución sigue un proceso distinto, y en general más simple que el caso anterior. En los dos siguientes, el objetivo es extraer la anilla o la cuerda con la bola grande que se encuentra en el centro.
Este otro puzzle tiene como objetivo deshacer el cruce de cuerdas que aparece en la parte derecha del juego, debiendo quedar el rompecabezas como aparece en la otra imagen.
El objetivo del siguiente es extraer la bola central del rompecabezas.
El rompecabezas que mostramos a continuación tiene un truco en su construcción. Mientras en los demás los cruces y uniones están a la vista, en este caso existe un lazo que queda oculto dentro de la bola grande y es el que permite resolver el problema. Es necesario que dentro de la bola se encuentre la disposición que vemos en la imagen.
En el siguiente modelo, debemos deshacer el cruce que aparece sobre la bola central.
Por último presentamos dos puzzles cuyo objetivo es extraer completamente la cuerda de la madera.
Estos últimos requieren mayor esfuerzo para resolverlos, pero la idea básica de manipulación es la misma que en los anteriores. Es posible encontrar más modelos en (Zang; 1996) de donde están sacados varios de los dibujos que hemos incluido.Aplicación didáctica. Ya hemos planteado anteriormente algunas de las relaciones existentes entre los rompecabezas topológicos y la resolución de problemas. Existen además otras posibilidades de aprovechamiento didáctico de estos juegos. La primera es su construcción. Todos son más fáciles de construir que de resolver. Por ello los alumnos pueden hacerlo sin dificultad. Puede usarse, como hemos visto en las fotografías, material fácilmente asequible o de reciclado. Cualquier listón de madera sirve. Las bolas pueden ser las de los respaldos frescos de los coches (que se encuentran con facilidad en los mercadillos), otros tipos de bolas (de collares viejos de fantasía) o cualquier anilla o elemento que pueda circular por las cuerdas y que no quepa por los agujeros que realicemos. Se trata de un ejemplo práctico de bricolaje matemático. Para su construcción se deben estudiar las medidas de la cuerda para que permitan los lazos y cruces que hay que realizar; así como el tamaño de los agujeros que, en el central, debe permitir pasar varias cuerdas a la vez. Cuando se aborda la resolución de estos rompecabezas, y en general de todos los manipulativos, es inevitable un periodo de tiempo de manejo del juego sin más reflexiones. Casi nunca servirá para resolver el problema, pero sí para conocer las limitaciones y vueltas al punto de partida que se producen. Por ello es aconsejable plantearse mentalmente por dónde podría ir la solución. También es interesante, para potenciar la visión espacial y realzar la capacidad de esquematizar los problemas de los alumnos, que dibujen el problema planteado y los pasos de la resolución, lo que además favorece las capacidades de representación gráfica. Hay que tener cuidado al manipular los rompecabezas pues suelen surgir dos problemas. Por un lado no es raro que, de pronto, nos encontremos con el problema resuelto sin saber cómo hemos llegado a él, con lo cual tenemos otro problema, y es reconstruir el juego sin conocer los pasos que hemos seguido, lo que muchas veces es más complicado aún (de lo que podemos dar fe). Otra dificultad es que se líe tanto la cuerda que llegue un momento en que quede irreconocible la situación inicial. En ese caso, si es posible (que no siempre lo es), debemos volver a las condiciones iniciales.Bibliografía
|
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |