35. CONCURSO DEL VERANO 2010
35. CONCURSO DEL VERANO 2010 |
 |
 |
 |
| Escrito por Mª Belén Garrido Garrido |
| Jueves 08 de Julio de 2010 |
|
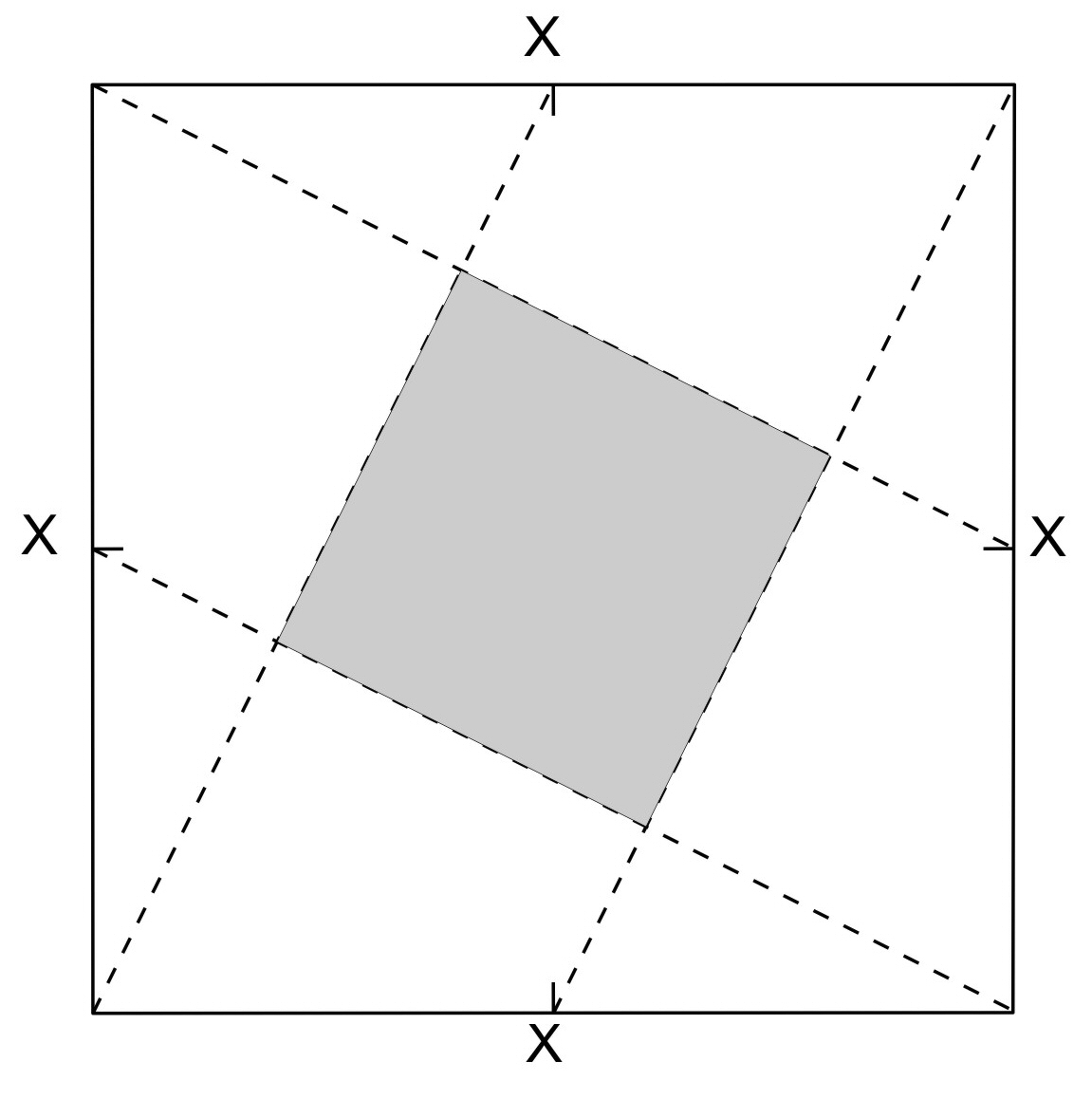
DOBLANDO CUADRADOS Si en un cuadrado de papel, mediante doblado, se marcan los puntos medios de los lados (x) y se hacen las dobleces indicadas en la figura se obtiene un cuadrado central cuya superficie es una quinta parte de la superficie del cuadrado de partida. Esto se demuestra muy fácil geométricamente, recortando el cuadrado por las líneas discontinuas con lo que se consiguen nueve piezas: un cuadrado, cuatro triángulos y cuatro trapecios. Reordenando los triángulos y trapecios dos a dos se forman cuatro cuadrados de las mismas dimensiones que la pieza cuadrada central.
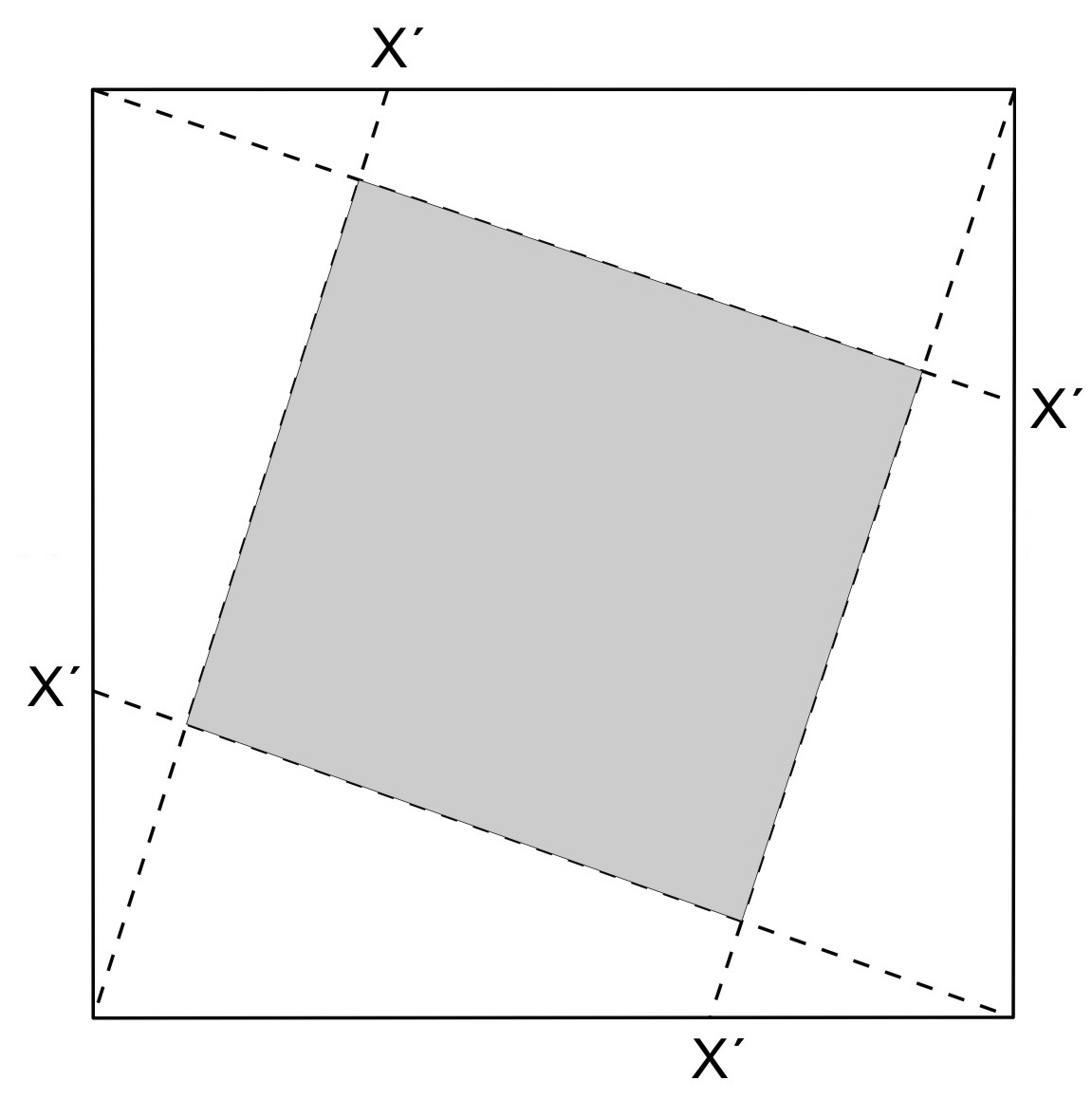
El reto de este verano: ¿Será posible conseguir mediante papiroflexia los puntos x', x'' y x'''? Estos puntos deben cumplir: a) un punto x' en los lados de un cuadrado de tal manera que doblando como se indica en la figura se consiga un cuadrado central cuya superficie sea la mitad de la superficie del cuadrado de partida. b) un punto x'' en los lados de un cuadrado de tal manera que doblando como se indica en la figura se consiga un cuadrado central cuya superficie sea la tercera parte de la superficie del cuadrado de partida. c) un punto x''' en los lados de un cuadrado de tal manera que doblando como se indica en la figura se consiga un cuadrado central cuya superficie sea la cuarta parte de la superficie del cuadrado de partida.
No es necesario que la demostración sea geométrica como en el caso del cuadrado cuya superficie es la quinta parte del cuadrado inicial. Si es necesario que los diagramas vayan acompañados de una demostración analítica. Podéis enviarnos vuestras soluciones a la dirección
Esta dirección electrónica esta protegida contra spambots. Es necesario activar Javascript para visualizarla
hasta el final del verano (21 de septiembre). Los participantes aceptan que DivulgaMAT pueda publicar las soluciones, independientemente del fallo del concurso. |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |