Cayetano Ramírez López - Lema 3
Cayetano Ramírez López - Lema 3 |
 |
 |
 |
| Jueves 08 de Mayo de 2008 | |||||||
Página 5 de 5
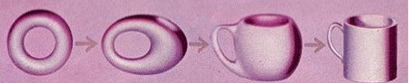
Lema 3: Las matemáticas, una herramienta para el arte La topología: las matemáticas de la distorsión La topología es un tipo de geometría que estudia propiedades de los objetos invariantes bajo la acción de transformaciones continuas. Una transformación continua sobre un objeto es algo que lo deforma, lo sube, lo baja, lo voltea, lo mueve de un lado a otro, pero no lo rompe ni lo pega sobre sí mismo. Por esta razón, se dice que un topólogo es una persona que no sabe distinguir entre un donut y una taza de café. En efecto, imaginemos que la rosquilla está hecha de goma elástica y observemos cómo se transforma en una taza de café sin romper, atravesar, unir o separar ninguna de sus partes.
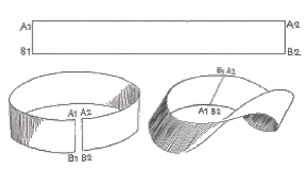
Superficies cerradas como la esfera y el toro, tienen dos caras, pero existen superficies con una sola cara. Un ejemplo es la banda de Möbius, descubierta por August Ferdinand Möbius, que se obtiene tomando una larga tira rectangular de papel y uniendo sus extremos después de darle media vuelta.
Si tratáramos de pintar un lado de un color y el otro lado de otro, llegaría un momento en que ambos colores chocarían, ya que, en realidad, estamos pintando el mismo lado. Esto pasa porque la banda de Möbius sólo tiene una cara. En matemáticas se dice que es un objeto no orientable.
El matemático alemán Felix Klein, siguiendo las directrices de Möbius, ideó una botella con una sola superficie, la llamada botella de Klein. Éste es un ejemplo de una superficie cerrada de una sola cara, sin ningún tipo de borde y que además no posee ni interior ni exterior. La botella de Klein también es una superficie no orientable.
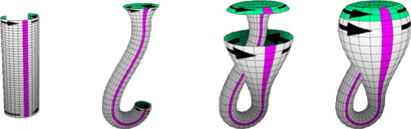
Para construir la botella de Klein, consideramos un cilindro, al que le hacemos un pequeño agujero. Introducimos entonces el otro extremo del cilindro por dicho agujero. Observemos que hemos cortado un trozo de nuestro espacio. Realmente la botella de Klein “no vive” en el espacio tridimensional, sino que lo hace en el espacio equivalente de cuatro dimensiones (esto es, en tal espacio podemos hacer el pegado de los extremos del cilindro sin necesidad de cortar ningún trozo de la botella).
|
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |








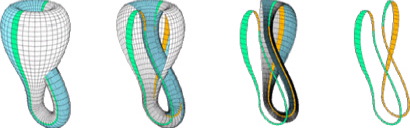
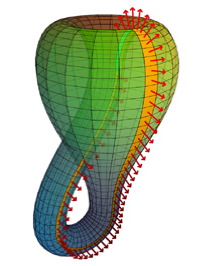 Un hecho curioso es que la botella de Klein se puede obtener pegando dos bandas de Möbius por sus bordes. Para convencerse de este hecho, basta efectuar un corte transversal a la botella.
Un hecho curioso es que la botella de Klein se puede obtener pegando dos bandas de Möbius por sus bordes. Para convencerse de este hecho, basta efectuar un corte transversal a la botella.