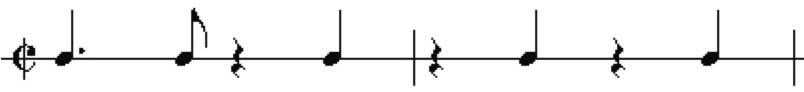31. (Diciembre 2011) Medidas matemáticas de síncopa (III)
31. (Diciembre 2011) Medidas matemáticas de síncopa (III) |
 |
 |
 |
| Escrito por Paco Gómez, Andrew Melvin, David Rappaport y Godfried Toussaint | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Viernes 02 de Diciembre de 2011 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Esta es la última entrega de la serie de tres artículos sobre la medida matemática de síncopa. En el primer artículo estudiamos el fenómeno de la síncopa desde el punto de vista puramente musical; en el segundo, revisamos las principales medidas matemáticas de síncopa y propusimos la nuestra propia; y en este artículo comparamos la efectividad de varias medidas sobre ritmos de clave tomados de tradiciones de música étnica. 1. Medición de la síncopas en ritmos En esta sección examinamos y comparamos las medidas de síncopa introducidas en los dos artículos anteriores probándolas con varios ritmos. Ciertamente, parece difícil seleccionar una familia de ritmos que uno pudiese calificar como representativa para semejante tarea. Una primera idea sería seleccionar ritmos que formen parte esencial de un género musical. En la llamada música étnica o música del mundo se pueden encontrar abundantes ejemplos de esto. En [3, 4], Toussaint recoge los principales ritmos de clave (o simplemente claves) de las tradiciones africana, cubana y brasileña, y lleva a cabo un estudio rítmico de dichas claves. En estas tradiciones hay un ritmo, que con frecuencia se toca en una campana de metal o en un par de claves de madera o en una caja china, y que se mantiene a lo largo de toda la pieza y cuyas funciones incluyen la estabilización rítmica y la organización del fraseo [2, 5]; este ritmo se llama de clave. En música clásica, el concepto más cercano al de clave es el de ostinato, como podemos apreciar, por ejemplo, en Purcell (Dido y Aeneas), Marin Marais (Sonnerie de Sainte Geneviève du Mont de Paris), Beethoven (la sonata para piano La tempestad opus 31, no 2), Ravel (Bolero), Holst (Marte en los Los planetas) y otros muchos casos. Las claves se pueden dividir en dos grupos atendiendo a su estructura métrica: claves binarias y ternarias, que se estudiarán separadamente. Ya que las claves se tocan en campanas o en claves de madera, que dan lugar a ataques más bien que a notas sostenidas, la medida de Keith se ha calculado teniendo en cuenta simplemente si D divide a S para determinar si una nota está a contratiempo o no; véase el anterior artículo de esta serie. 1.1. Ritmos binarios Las seis claves binarias fundamentales son: shiko, son, rumba, soukous, bossa-nova y gahu. Refiérase el lector a [3] y a la bibliografía contenida en ese artículo para una completa información sobre ritmos de clave. En la figura 1 podemos ver que la partitura musical y las correspondientes medidas de síncopa calculadas con la medida de Keith, el índice de contratiempo y la medida DPNP.
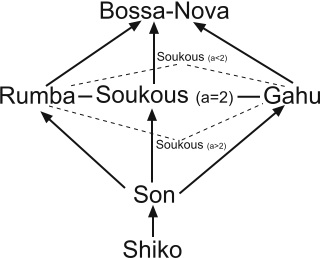
Figura 1: Ritmos binarios. Claramente, shiko es la menos sincopada; la clave son es más sincopada que la shiko, y la rumba más sincopada que la son. Sin embargo, no está claro qué ritmo entre la rumba, el soukous y el gahu es el más sincopado. Bossa-nova es ciertamente la más sincopada. En general, las tres medidas apoyan estas conclusiones, aunque hay algunas divergencias que nos permiten extraer conclusiones interesantes acerca de su utilidad. La medida de Keith en la mayoría de los casos devuelve valores razonables para la medida de la síncopa, aunque no entra en detalles sutiles. Por ejemplo, la bossa-nova se siente más sincopada que cualquier otro ritmo, pero la medida de Keith le asigna los mismos valores que al soukous y el gahu. Sorprendentemente también, asigna la misma cantidad de síncopa a la rumba y el son. Es algo extraño que esta medida devuelva un valor de 3 para el motivo rítmico clásico-2, poniéndolo al mismo nivel que la bossa-nova o el gahu. El índice de contratiempo parece estar más cerca de la percepción humana de la síncopa que la medida de Keith, aunque también da lugar a conclusiones dignas de debate. Por ejemplo, gahu recibe valor 1, pero se siente más sincopado que el son, que también tiene valor 1. Es desconcertante que los dos motivos clásicos obtengan una puntuación mayor que cualquiera de las restantes claves, incluida la bossa-nova. La medida DPNP sugiere conclusiones razonables y en general muestra una mayor coincidencia con la percepción humana de la síncopa. La bossa-nova alcanza la mayor puntuación en el grupo. La medida pone a la rumba, el soukous y el gahu en la misma categoría. En un nivel inferior, encontramos al son, y debajo de este, el shiko, el ritmo menos sincopado; véase la figura 3. Nótese que sin la corrección del número de notas un ritmo con tan poco nivel de síncopa como el motivo rítmico clásico-1 obtendría una puntuación tan alta como la clave gahu, que es mucho más sincopada. Véase la columna que contiene la suma ∑ xD(x) en la figura 1. Volvamos al delicado asunto de elegir los pesos para la medida DPNP. En la definición de of D(x), cuando una nota x cruza una parte fuerte y termina antes de la siguiente parte fuerte, entonces la distancia es
Considérese el grafo que se muestra en la figura 3. Ahí cada nivel designa una medida de síncopa. No importa qué valores de a,a > 1, se elijan, el orden se preservará, excepto por soukous. Unas pocas operaciones algebraicas con desigualdades muestran enseguida que esta afirmación es cierta. Con respecto al soukous, si 1 < a < 2, entonces soukous sería más sincopado que el gahu y la rumba (esta situación se muestra en la figura 3 con la línea a puntos); si a = 2, entonces los tres serían igualmente sincopados; finalmente, si a > 2, entonces soukous sale como el menos sincopado (véase la otra línea de puntos en la figura 3). 1.2. Ritmos ternarios En el artículo anterior introdujimos las diez claves fundamentales son: soli, tambú, bembé, bembé-2, yoruba, tonada, asaadua, sorsonet, bemba y ashanti. Véase [4] y sus referencias para una descripción completa de estos ritmos. Las partituras y los correspondientes valores del índice de contratiempo y de la medida DPNP se muestran en la figura 4.
De nuevo, ambas medidas parecen tener sentido de manera global para estos ritmos. En el caso del índice de contratiempo solo el bembé obtiene la máxima puntuación, mientras que la medida DPNP tiene al bembé, al yoruba, al sorsonet y al ashanti como los ritmos más sincopados. Los diez ritmos de clave pertenecen a tres collares (patrones) canónicos distintos [1, 4]. El patrón canónico I corresponde al sorsonet solo; el patrón canónico II genera soli, tonada y asaadua; el patrón canónico III incluye el bembé, el bembé-2, el tambú, la tonada, el yoruba, la bemba y el ashanti. El índice de contratiempo clasifica los ritmos originados por los patrones canónicos I y II como los menos sincopados. Todos los ritmos de clave generados por el patrón canónico III, excepto el bembé, cuyo índice de contratiempo es el más alto, irían en segundo lugar. La medida DPNP agrupa los ritmos de diferente manera. El grupo con el mayor valor está constituido por el bembé, el yoruba, el ashanti y el sorsonet; en el siguiente grupo encontramos el tambú, el bembé-2, la bemba, el soli, la tonada y la asaadua. Esto último grupo comprende todos los ritmos del patrón canónico II más el tambú, el bembé-2 y la bemba. La pregunta que surge de modo natural es cómo construye la medida DPNP esta clasificación. Observemos que todos los ritmos en el grupo menos sincopados tienen tres notas en parte fuerte y solo una nota que cruza la parte fuerte restante. Por el contrario, los ritmos más sincopados tienen dos notas en parte fuerte y otras dos notas que cruzan una parte fuerte. Sin embargo, el índice de contratiempo no detecta esta situación y lleva al tambú, al bembé-2 y a la bemba del grupo menos sincopado al más sincopado. Por el contrario, el índice de contratiempo lleva el sorsonet, que es considerado por la medida DPNP como sincopado, al grupo menos sincopado. La comparación entre los ritmos de clave y mótivos rítmicos de la música clásica produce resultados más consistentes que en el caso de las claves binarias (véase la columna que contiene la suma ∑ xD(x) en la figura 4). El índice de contratiempo considera los dos motivos tan sincopados como el yoruba o el ashanti, pero esto parece erróneo. La medida DPNP detecta correctamente que son menos sincopados que los ritmos de clave. Los pesos en la medida DPNP no tiene influencia en el orden relativo de los ritmos ternarios, porque todas las medidas son de la forma 3a + ci, donde ci es una constante aditiva para el ritmo i. 2. Conclusiones finales Vamos a extraer conclusiones de los resultados empíricos obtenidos en la sección anterior; empezaremos por los puntos débiles de cada medida. Los mayores inconvenientes de la medida de Keith son: (1) No se puede medir ritmos cuyas métricas no tengan un número de notas que no sea una potencia de 2; (2) No se puede usar para medir ritmos irregulares; (3) La elección de los pesos es subjetiva; (4) Muestra una coincidencia limitada con la percepción humana de la síncopa. Con respecto al índice de contratiempo, encontramos los siguientes inconvenientes: (1) Es limitada en su aplicación, ya que para métricas con un número primo de notas todas las notas están a contratiempo; (2) No se puede usar para medir ritmos irregulares; (3) No mide la síncopa en toda su generalidad. Por ejemplo, en un compás de 12/8, las posiciones a contratiempo son 1,5,7,11. Sin embargo, un ritmo puede ser muy sincopado sin tener notas en esas posiciones; (4) Es independiente del número de notas. Por ejemplo, el bembé y [x x . . . x . x . . . x] tienen contratiempo 3, pero un número diferente de notas; (5) Aunque muestra más coincidencia con la percepción humana de la síncopa que la medida de Keith, esa coincidencia es todavía limitada. El único inconveniente que la medida DPNP parece tener es la ambigüedad en la elección de los pesos. Sin embargo, la elección de los pesos no parece tener un efecto en los resultados finales tan dramático como en el caso de la medida de Keith. Un algoritmo mejor para elegir los pesos sería altamente deseable. Finalmente, concluimos que la medida DPNP tiene mayor coincidencia con la percepción humana de la síncopas que el resto de las medidas y también un mayor grado de aplicación. Cerramos este artículo con unos cuantos problemas abiertos. Sería interesante generalizar la medida de Keith de manera que admitiese métricas más generales. Otra dirección de investigación sería la generalización del índice de contratiempo para que contemplase satisfactoriamente el caso de los números primos. Con respecto a la medida DPNP, nos gustaría obtener resultados empíricos adicionales -quizás en forma de experimentos con sujetos- de manera que los pesos se obtuviesen de manera más precisa. Agradecimientos Los resultados de este artículo se obtuvieron en el Second International Workshop on Computational Music Theory organizado por el Departamento de Matemática Aplicada en la Escuela Universitaria de Informática de la Universidad Politécnica de Madrid en junio de 2004. Nos gustaría dar las gracias a Giovanna Farigu y Shima Kobayashi por sus clarividentes discusiones sobre el problema de la síncopa. Bibliografía [1] Keith, M.; From Polychords to Pólya: Adventures in Music Combinatorics, Vinculum Press, Princeton, 1991. [2] Ortiz, F.; La Clave, Editorial Letras Cubanas, La Habana, Cuba, 1995. [3] Toussaint, G. T.; A Mathematical Analysis of African, Brazilian, and Cuban Clave Rhythms, Proceedings of BRIDGES: Mathematical Connections in Art, Music and Science, pp. 157-168, Towson University, Towson, MD, 2002. [4] Toussaint, G. T.; Classification and Phylogenetic Analysis of African Ternary Rhythm Timelines, Proceedings of BRIDGES: Mathematical Connections in Art, Music and Science, pp. 25-36, Universidad de Granada, Granada, 2003. [5] Uribe, E.; The Essence of Afro-Cuban Percussion and Drum Set, Warner Bros., Miami, 1996. |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |