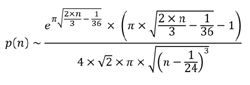El ojo de Shiva, el sueño de Mahoma, Simbad... y los números
El ojo de Shiva, el sueño de Mahoma, Simbad... y los números |
 |
 |
 |
Con subtítulo La ruta del cero y los otros viajeros de Oriente, abrí este libro por primera vez poco después de su publicación y quiso el azar que fuese por la página 222, que contiene una extraordinaria fórmula. Allí se cuenta el episodio de la colaboración entre Hardy y Ramanujan sobre el problema de determinar una fórmula para el número p(n) de particiones de un número natural n y se consigna (v. recuadro) la aproximación asintótica que obtuvieron en 1918:
Tres páginas más adelante leemos que pensaban que los mismos métodos podrían refinarse para obtener una fórmula exacta; que fueron Rademacher y Selberg quienes materializaron (independientemente) esta predicción (1937); y que muchos años después Selberg comentó (1987, con ocasión del centenario del nacimiento de Ramanujan): «si Hardy hubiera confiado más en Ramanujan, tengo pocas dudas de que habrían acabado encontrando la fórmula». Aunque el título, salvo por la palabra «números», parece disjunto de lo que acabamos de referir, me prometí leerlo en cuanto tuviera tiempo. Además de imaginar que encontraría muchas sorpresas, pesó también esta irónica manifestación del autor: «merece la pena escribir aquí esa fórmula, aunque sólo sea por lo exótica que resultará a un lector no matemático» (énfasis mío). No ha sido hasta las pasadas vacaciones navideñas en que pude realizar mi promesa. Resultado: es una obra poliédrica, en la que se trenzan hilos de muchos tipos para trazar la evolución de la representación de los números y, en particular, del actual sistema de numeración decimal, que es «de origen indio [hacia mediados del primer milenio], aunque el cómo, cuándo y porqué de su nacimiento en la India es algo que ha quedado cubierto por la bruma de los tiempos. Los registros escritos son tan escasos y dispersos que sólo permiten una mirada imprecisa sobre el desarrollo de tan fundamental acontecimiento científico» (p. 118, énfasis mío). «El viaje de los números fue largo, no sólo por los muchos siglos que le tomó hacerlo, sino también por la amplitud y diversidad de la ruta realizada a través de un territorio que va de la India a España, pasando por Oriente Próximo y ambas orillas del Mediterráneo» (p. 10). El libro está estructurado en cuatro capítulos (India, Ramanujan, Por tierras del islam y La Ruta de la Seda), con un Delantal (tres páginas), una Coda (seis páginas) y una breve nota de Final de Trayecto. Es a la vez una novela (sobresale Cristina, coprotagonista con el autor/narrador) y un ensayo sobre historia de la ciencia, de las matemáticas y la astronomía en particular, con ribetes de reflexión filosófica. Es un libro de viajes que contiene interesantes observaciones sobre lógica, lingüística, literatura y cine, geografía, religiones, política y relaciones interculturales (frecuentemente conflictivas),… adornadas a menudo con sugerentes apuntes gastronómicos. Lo apreciarán todos cuantos anhelan encontrar, como Remo Bodei al referirse a la filosofía, «el sentido y las conexiones en el todo que la ciencia pierde al especializarse». También aquéllos para quienes tienen un profundo sentido preguntas como las siguientes: «¿Por qué seguimos usando miles de lenguas distintas y varios sistemas de símbolos para representarlas y, en cambio, sólo una manera para escribir los números?» (p. 10); «¿Y si al final todo se redujera a contar, ya sean números o cuentos?» (p. 489). Esta segunda pregunta encierra la esencia del hilo que entrelaza los dos significados principales de contar y que pone de manifiesto la evolución entretejida de los algoritmos numéricos y algebraicos con cuentos como los de Las mil y una noches, y a lo largo de los mismos caminos. En la página 328 se refieren unos acontecimientos que mil quinientos años después nos resultan fatídicamente familiares: «Cuando el emperador Justiniano decretó en 529 el cierre de todas las escuelas filosóficas griegas por considerarlas paganas —incluida la Academia de Platón y los centros científicos de la Biblioteca de Alejandría—, buena parte de los filósofos y científicos afectados buscaron refugio en Persia de los sasánidas». Los conocimientos de esta diáspora fueron asimilados por los árabes, que los fusionaron con la ciencia griega e india, en una eficaz síntesis de teorías y aplicaciones que fueron ajenas al mundo occidental durante largos siglos.
Antonio J. Durán es catedrático de Análisis Matemático en la Universidad de Sevilla y es autor de una extensa obra que incluye ediciones de Arquímedes, Newton y Euler (SISIUS). También ha publicado dos novelas: La luna de nisan (2002) y La piel del olvido (2007). (Reseña aparecida en el Boletín de la RSME nº 389) Materias: Números, cero, sistema numeración, historia, relato.
Autor de la reseña: Sebastià Xambó Descamps (Universidad Politécnica de Cataluña). |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |