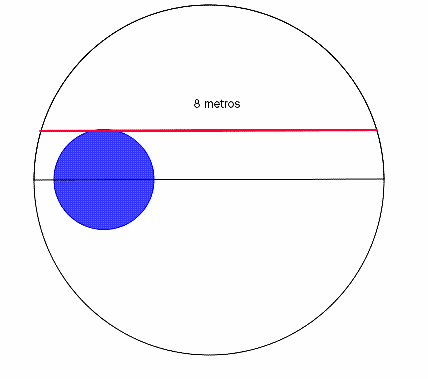
Queremos medir la superficie de un campo circular que  tiene un pozo de agua en su interior

(el centro del pozo está sobre el diámetro de la circunferencia grande, dibujado en negro)

El pozo se muestra en azul y también tiene forma circular (se muestra un esquema del dibujo).

Sabemos  que la cuerda( en rojo)  mide 8 metros , y  es  paralela al diámetro de la circunferencia grande

y tangente a la circunferencia pequeña.  Con ese único dato

¿Cuál es la superficie del círculo grande, excluyendo el área del pozo circular?

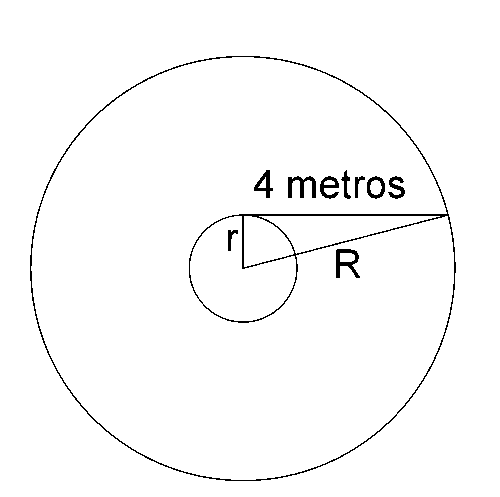
Es claro que si el pozo lo pudiesemos mover de manera que las dos circunferencias

fuesen concéntricas, el área pedida sería la misma. Evidentemente el problema es más sencillo, pues únicamente

aplicando el teorema de Pitágoras podemos calcular el área pedida, que por otra parte coincide con

la corona circular, cuya área es  A = p( R²-r²)=3,14(16)= 50, 24 metros cuadrados