43. SOLUCIÓN CONCURSO DEL VERANO 2012
43. SOLUCIÓN CONCURSO DEL VERANO 2012 |
 |
 |
 |
| Escrito por José Ignacio Royo Prieto y Mª Belén Garrido Garrido | ||||||||||
| Viernes 07 de Septiembre de 2012 | ||||||||||
|
ENUNCIADO Es posible diseccionar un hexágono regular y con las piezas formar un rectángulo áureo (Capo Dolz, M. 2011)
El reto de este verano es conseguir marcar las líneas de disección del hexágono mediante papiroflexia.
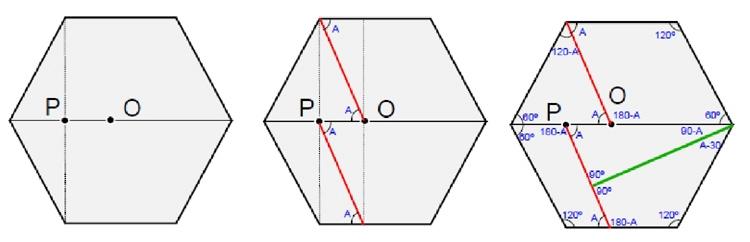
La solución ganadora este año ha sido la de Paz Carbajo, ¡Felicidades, Paz! Os la podéis descargar abajo. La presentación es fabulosa y las explicaciones detalladas. Queremos hacer unas aclaraciones que pueden ayudar a comprender la naturaleza del problema planteado. En primer lugar, no todo es lo que parece, y la vista puede hacernos pensar que en la partición del hexágono del dibujo se utiliza el punto medio del hexágono. Si así se hiciera, el rectángulo que se formaría no sería áureo. Algunas soluciones que hemos recibido han señalado este hecho, y proporcionado una manera de construir esa partición con papiroflexia. Como todas esas construcciones nos parecían interesantes aunque el rectángulo no fuera áureo, hemos optado por publicarlas. Pero si no nos dejamos traicionar por los sentidos y nos fiamos de que el rectángulo resultante es áureo (como hace Paz en su solución), se puede encontrar la partición deseada. La siguiente construcción puede ayudar a comprender el problema: partimos de un hexágono regular y fijamos, sobre la diagonal que se muestra, el punto P (que está, como vemos, determinado) y el punto O (que es un punto arbitrario, cercano al centro). A partir de estos dos puntos, quedan determinadas las líneas rojas de la construcción, y el ángulo que hemos llamado A. En la última ilustración se traza una nueva línea, de color verde, perpendicular a la línea roja, obteniendo una partición del hexágono similar a la de la figura del enunciado.
Lo hermoso del asunto es que, independientemente del punto O escogido, las piezas que obtenemos van a poder reordenarse para configurar un rectángulo, como en el dibujo del enunciado. No es un hecho evidente a simple vista, pero se puede comprobar fácilmente, dado que los ángulos son compatibles (los hemos detallado en la última figura) y las longitudes, también. El caso es que el rectángulo obtenido no tiene por qué ser áureo. De hecho, como hemos comentado, si O es el punto medio del hexágono, el rectángulo no será áureo. En la solución de Paz se calcula cuál tiene que ser ese punto para que el rectángulo resultante sea áureo. Más aún: se proporciona un método de plegado para obtener esas marcas. Una vez más, muchas gracias a todos los que habéis participado, por enviarnos vuestras soluciones. Solución ganadora:
Soluciones con rectángulo no áureo:
|
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |