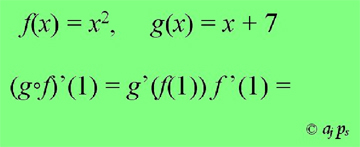73. La Cuadratura del Celuloide
73. La Cuadratura del Celuloide |
 |
 |
 |
| Escrito por Alfonso Jesús Población Sáez | |||
| Viernes 05 de Octubre de 2012 | |||
|
Dedicamos la reseña de este mes a describir este libro publicado recientemente junto a una entrevista realizada a su autor a la que gentilmente nos ha respondido. Después, a modo de entretenimiento, se incluyen algunos de los jeroglíficos cine-matemáticos que diariamente han venido apareciendo en Facebook y que tanta aceptación están teniendo.
Como acercamiento general digamos que el libro está dividido en ocho capítulos, que por supuesto habla de matemáticas (mejor de cultura matemática, porque no hay operaciones, ni demostraciones; es un libro divulgativo, no técnico), pero que no sólo lo hace de su relación con el cine (que también), sino con las más variadas manifestaciones artísticas y culturales que componen el conocimiento humano (música, arquitectura, pintura, escultura, literatura, otras disciplinas científicas, etc.). Respecto al cine, tampoco se conforma con exponer las consabidas citas explícitas que todo el mundo reconoce como matemáticas, sino que va un poco más allá, buscando las relaciones menos distinguibles, más filosóficas. Es un texto espléndidamente documentado, con una cantidad inagotable de referencias a otras fuentes, de muchas de las cuales, cuando las ideas o frases son razonablemente breves, son reproducidas para que el lector constate de lo que se habla. Además se incluyen a pie de página, no al final del libro, lo que evita el incómodo ejercicio de ir saltando de un lado para otro. Si la referencia es a un matemático famoso o a un resultado, la cita es sintética, yendo a la información más relevante que impida distraernos demasiado. El mayor inconveniente a mi juicio (que para otros puede no serlo) es la dificultad en la localización concreta de datos, ya que salvo la división de los capítulos comentada, los párrafos se desarrollan uno tras otro, sin nada que indique un cambio de tema o de dirección. Además escasean las ilustraciones que en muchas ocasiones echas de menos (referencias por ejemplo, a un cuadro, una escultura, un dibujo, etc.) pero es disculpable, so pena de encarecer la edición, incrementar el ya de por sí amplio número de páginas, por no hablar de los derechos de autor que se precisan hoy día hasta para incorporar una foto del vecino de arriba. El primer capítulo es, como indica el propio texto, “un capítulo de marcado carácter generalista, con referencias matemáticas en cualquier ámbito de la cultura”. Su objetivo es mostrar que, a pesar de que se considere a la matemática y a los matemáticos como una “fauna minoritaria”, lo cierto es que ha sido y es una disciplina muy activa y relevante para la creación artística. El segundo capítulo, “La ecuación completa del cine” aborda cómo ha incidido la tecnología en la realización cinematográfica, desde los inicios del cine a los modernos efectos especiales, una ostensible mejoría, posible gracias al desarrollo de la ciencia. Por otra parte el cine ha servido de vehículo de divulgación científica y educativa, tanto a nivel microscópico como macroscópico. Se indican los precursores de este tipo de cine, se exponen algunos ejemplos concretos de esta mejora en la realización técnica cinematográfica, y posteriormente nos adentramos en la industria de Hollywood. El capítulo finaliza con una pequeña incursión en lo que se conoce como cine experimental, una especialidad en la que las matemáticas han aportado, sobre todo a nivel gráfico, un montón de nuevos caminos con los que, valga la redundancia, experimentar. El título del capítulo hace referencia a una frase de la película El último magnate (The Last Tycoon, Elia Kazan, EE. UU., 1976) y al título original del libro La verdadera historia de Hollywood (The Whole Equation), escrito por David Thomson y editado en castellano por T&B en 2006, una de las muchísimas referencias a las que acude el autor. El tercer capítulo, Misteriosa forma del tiempo, se dedica a la relación entre la música, el cine y las matemáticas, con numerosas referencias a estudios de gran cantidad de autores. Música abstracta, música electrónica, música y arquitectura (en este apartado no podía faltar una incursión a los mundos imposibles de M.C. Escher), música estocástica (cálculo de probabilidades aplicado a la composición musical), compositores que utilizan las matemáticas para componer, ejemplos de letras de canciones comerciales en las que aparecen las matemáticas, son algunos de los temas tratados, que nos llevan a concluir, por un lado, la influencia de la música en el cine hasta el punto de que el producto final sería diferente dependiendo de la música utilizada, y por otro, acercarnos a tratar de determinar cómo podría ser el sonido de la matemática. Ruta hacia el reino de las hadas (frase del director de cine francés René Clair: “Méliès es el inventor del espectáculo, ruta hacia el reino de las hadas, entre las tiernas estrellas y los soles sonrientes”) es el título del siguiente capítulo dedicado a la ciencia ficción en la literatura y el cine, y a la influencia del progreso científico y tecnológico en estas disciplinas. Repasando los orígenes de este género (la Utopía de Tomás Moro, el Somnium de Kepler, el viaje a la Luna de Cyrano de Bergerac, las obras de Julio Verne, el Frankenstein de Mary Shelley, etc), se expone una visión pesimista de escritores y directores de cine sobre el futuro de la tecnología. Entre las manifestaciones más elocuentes se encuentra la dada por el protagonista de la novela Tu nombre envenena mis sueños (Joaquín Leguina, 1992): El atractivo de la investigación radica en su inutilidad. Por eso me dedico a las Matemáticas, una ciencia inútil […] Un gran matemático llamado Gauss se congratulaba de que existiera una ciencia, la suya, cuyas remotísimas repercusiones sobre las actividades humanas le permitían mantenerse noble y limpia de toda culpa. Gauss dijo: si las Matemáticas son la reina de todas las ciencias, la teoría de números es, a causa de su suprema inutilidad, la reina de las Matemáticas. Resulta llamativo, a pesar de ello, cómo en ocasiones, las matemáticas se han puesto al servicio de la intransigencia y el despotismo, citándose algunos de los ejemplos más representativos. Posteriormente, se recorren algunos de los tópicos matemáticos más visitados por los seguidores de este género: el teorema de Pitágoras, las matemáticas como medio de comunicación extraterrestre, la banda de Möebius, el círculo y su imposible cuadratura, los problemas sin resolver (conjetura de Poincaré, el último teorema de Fermat) como fuente de inspiración, y entremedias un apartado dedicado a las falsificaciones y las matemáticas como medio para poder detectar algunos de esos fraudes. El capítulo concluye con citas y ejemplos de escritores de ciencia ficción que han utilizado las matemáticas y la ciencia en general en sus argumentos, algunos con orientación matemática que se han animado a escribir obras de ciencia ficción. El quinto capítulo (El pulso eterno de una circunferencia) se dedica a describir algunas escenas cinematográficas en las que aparecen cuestiones de aritmética básica, para después abordar la técnica del montaje milimétrico cuyos máximos exponentes han sido los realizadores rusos, a los que posteriormente imitaron otros. En los dos siguientes capítulos, el autor nos sorprende sustituyendo por símbolos matemáticos aquellas cadenas de letras en las que aparecen expresados explícitamente números u operaciones (so*tan, hela2, 1s, ¸ga2, etc.). El primero, Cuanto + conozco las letras, + quiero los números, está dedicado a películas en las que parecen números o fórmulas en sus títulos o argumentos. Después se repasan aquellas producciones en las que aparecen científicos, en principio reales (biopics) y después imaginarios, inventados. De ahí llegamos a películas en con un argumento matemático más complejo que las tratadas hasta este momento, volviendo a la planificación milimétrica de las películas (entroncando por ello con lo hablado en el capítulo anterior sobre el montaje, la edición final de la película). El título del capítulo alude en este caso a una frase de Tres Tristes Tigres (1967) de Guillermo Cabrera Infante, que a su vez se basa en la conocida frase atribuida a Lord Byron, “Cuanto más conozco a los hombres, más quiero a mi perro”.
Para acabar, El cine que reinventa el cine (frase que Guillermo Cabrera Infante, uno de los escritores más referenciados por el autor junto a Arthur C. Clarke, utiliza para describir Reservoir Dogs y Pulp Fiction en su libro Cine o sardina, 1997), se dedica a explorar nuevas formas de narrar las películas, herederas directas de los procesos no lineales. Entrevista a José Luís López Fernández, autor de “La cuadratura del celuloide” Ante todo nos gustaría agradecerte que hayas atendido nuestra petición, más en estas fechas de inicio de curso, en la que todos estamos tan atareados. DivulgaMAT: La primera cuestión es casi obligada: ¿Qué te llevó a escribir una obra como “La cuadratura del celuloide”? José Luís López: Una conjunción de múltiples factores: la necesidad de explorar el terreno, de saber y de comunicar, en este caso por medio de la escritura; el desafío de transmitir el potencial de emoción que encierra el visionado de una buena película, la lectura de un libro o la contemplación de una pieza de arte; la terca voluntad de acercar la ciencia, particularmente las matemáticas, a todo lector que quiera aproximarse a ella desde una perspectiva ampliamente cultural, desmitificada y cotidiana. DivM.: Ver publicado un proyecto como éste no está exento de dificultades. ¿Con cuales te encontraste y cómo las resolviste? J.L.L.F.: La primera dificultad, y a la postre la más provechosa, fue convencer a Inma, tan colega de cuadraturas y celuloides como buena amiga, para que se ocupara del prólogo. Eso era lo más importante, desde el tiempo y la distancia que nos separaba, para mí y para mi proyecto. Luego fueron llegando los sinsabores esperados (y lógicos) cuando uno ejerce de piloto kamikaze en una guerra que no es la suya, todos ellos relacionados con la reacción del mercado editorial ante una propuesta injustamente minoritaria y, por tanto, relegada a galeras desde el momento mismo del parto. Debo decir que, salvo muy contadas excepciones, la respuesta de la mayor parte de las compañías editoriales con las que he contactado ha sido rápida, amable y agradecida. Ante esto, la única solución posible pasaba por (i) abandonar el proyecto, (ii) armarme de paciencia y esperar (¿indefinidamente?) a que la ciencia se pusiera de moda (y cierto es que no corren buenos tiempos para que ello suceda), o (iii) ser mi propio editor. Y opté por (iii). DivM.: Has dividido la obra en ocho capítulos. Descríbenos brevemente qué criterio seguiste. J.L.L.F.: Realmente me habría gustado que no existiera tal división capitular en La cuadratura, pero comprendo que ello habría hecho terriblemente compleja su lectura. Habría preferido eliminar el corsé que los capítulos imponen a la obra y agitar profusamente el contenido antes de servirlo. No obstante me faltó arrojo para hacerlo, incluso cuando ya sabía que el libro vería la luz siguiendo un formato de autoedición, en un intento de esquivar la repulsión apriorística de los lectores potenciales de la obra. Puestos a "ordenar" los contenidos, el primer capítulo actúa a modo de introducción general (haciendo especial hincapié en los terrenos artístico y literario), mientras que los siete restantes pretenden agrupar en torno a ellos ciertas unidades temáticas, en un sentido amplio de la expresión, que indagan en los ámbitos de la Historia del cine, la música, la ciencia ficción, la matemática aplicada al discurso cinematográfico (desde el montaje de un filme a la labor de la crítica especializada), la poesía y el universo de lo no lineal. DivM.: Cuando un lector cualquiera se dispone a leer el libro, se tiene la sensación de entrar en capítulos inmensos en los que, salvo por el índice de películas, no es sencillo localizar algo concreto. ¿Has sido consciente de esto a la hora de decidir la edición final? ¿Cómo aconsejas al lector interesado que se disponga ante el libro o busque la información en la que esté interesado? J.L.L.F.: Absolutamente. Como bien apuntas, el índice de películas (y novelas, canciones, directores, intérpretes, ensayos, etc.) es la única herramienta de ayuda prevista para el caso en que el lector estuviera interesado en evadirse de la anarquía intencionada del texto para buscar puntualmente la información relativa a un título o un autor. De hecho, entiendo que una de las posibles lecturas de la obra –la más ventajista, de hecho, si uno no estuviera dispuesto a atravesar a pie esta jungla casi periodística sino solamente a sobrevolarla–, consiste en ir de adelante hacia atrás, dejándose arrastrar por las páginas del libro según los ítems de interés de cada lector. Ahora bien, el espíritu de la obra es exactamente el contrario: difuminar la luz de la ciencia a lo ancho y largo de la eclosión cultural del pasado siglo y confundirlo todo un poco, sin aislar ninguna disciplina de sus hermanas, aunque sea el cine el vehículo elegido para conformar la columna vertebral de La cuadratura. DivM.: Cuando uno escribe a veces se piensa en los potenciales lectores ¿A quien va dirigido La cuadratura del celuloide? ¿Quién esperas que lo disfrute? ¿Qué deseas que encuentre o que quieres mostrarle? J.L.L.F.: En este caso era realmente complicado diseñar un perfil mental del lector potencial. Me explico: es perfectamente plausible que a alguien le guste el café o la leche por separado y que, sin embargo, no tolere el café con leche. Con ello quiero decir que el lector interesado únicamente en una de las dos disciplinas que articulan el libro, matemáticas o cine, cine o matemáticas, bien pudiera encontrarlo deficitario (y con razón) en muchos aspectos; recíprocamente, podría suceder asimismo que un lector interesado en la integración de ambas disciplinas no se hubiese arriesgado jamás a leer una obra que tratara de una de ellas en exclusiva. En este sentido, las dos posibles rutas de lectura señaladas en la respuesta anterior –la directa y la inversa– creo que facilitan el hecho de que cada lector consiga encontrar suficiente acomodo para ver satisfecha su motivación principal, cualquiera que ésta sea. El disfrute, en cualquier caso, depende de las inquietudes científicas y cinematográficas del lector y de sus ganas de aprender a conjugarlas. Finalmente, lo que pretendo mostrar al lector (y lograr que éste sea capaz de identificar) es que la ciencia constituye un ingrediente principal de la cultura universal y es consustancial a ella, partícipe de su evolución y depositaria de su destino. DivM.: El libro en realidad no está exclusivamente dedicado al cine: hay muchas referencias a otros aspectos de la cultura como la música, la literatura, etc. ¿Por qué entonces el título de “La cuadratura del celuloide? J.L.L.F.: Bien cierto. Ya desde el prefacio intento aclarar este punto cuando afirmo que, para mi suerte o desgracia, no soy capaz de concebir el cine como un fenómeno cultural aislado, independiente y descontextualizado del resto de las expresiones artísticas. Es necesario, entiendo, adentrarse en otros terrenos para comprender el alcance de un abigarrado nudo de influencias en el que la ciencia tiene mucho que decir. Aun así –y vuelvo a lo anunciado en el prefacio– elijo en todo caso como medio de canalización, para este recorrido babélico por la matematización de la cultura del siglo XX, la actividad cinematográfica. El título, por consiguiente, hace referencia a la matemática a través del conocido problema de la cuadratura del círculo, y al cine a través del celuloide, aquel material que sirvió de soporte a la película (tanto fotográfica como cinematográfica) en la primera etapa del medio. DivM.: Los capítulos 6 y 7 se presentan de un modo un tanto singular, sustituyendo por sus símbolos correspondientes las combinaciones de letras en las que aparecen números u operaciones matemáticas. ¿Por qué precisamente esos capítulos? ¿Tiene alguna intención concreta? J.L.L.F.: La razón estriba en que ambos capítulos aglutinan contenidos fundamentalmente relacionados, en mayor o menor medida, con la aritmética, por lo que los símbolos asociados a operaciones estándar, así como los guarismos, son entendidos desde una perspectiva matemática a pesar de formar parte de un texto. La única intención de esta "incomodidad" reside, como dije antes, en mi voluntad de confundirlo todo un poco más entre sí (el cine con todas las manifestaciones artísticas y culturales que lo envuelven, la ciencia con la poesía, los números con las letras, la música con los teoremas… ciñéndome nuevamente a lo sostenido en el prefacio). Pongamos que no se trata más que de una especie de juego de ingenua raigambre oulipiana. DivM.: Cuando uno empieza a escribir un libro de este estilo y busca información, debe recurrir a muchas fuentes. ¿Qué es lo que más te ha sorprendido, agradado, desagradado, etc., de lo que has encontrado y escrito? J.L.L.F.: Han sido cerca de siete años de trabajo (enormemente placentero) desde que comenzara a divisar un proyecto sobre el que no sabía si se podrían escribir más de diez páginas, y al final han resultado ser más de quinientas. Resulta ciertamente fascinante bucear (con Nemo) entre las técnicas que acompañan el diseño y puesta en marcha de una película de animación; verificar el ingente número de ecuaciones paramétricas que se escondían detrás de los primeros filmes experimentales de los años sesenta; imaginar a Hedy Lamarr patentando un sistema de control remoto por radiofrecuencias; descubrir que el hijo de John Wayne suspendió las matemáticas en la academia de cadetes de West Point en una vieja película de John Ford; o admirar que toda una leyenda del cine como Frank Capra considerara las matemáticas como uno de los tres lenguajes universales, junto a la música y el cine. Todo ello unido a la gran cantidad (en comparación con lo esperado) de gente del cine que está vinculada, por formación o por afición, a alguna rama científica y, en buena parte, a las matemáticas. Por comentar también algo que me inquieta a este respecto, destacaría el estereotipo de malvado, chiflado o idiota que parece reservado a los científicos en el cine, a pesar de que alguno de estos retratos haya dado lugar a personajes inolvidables y a filmes de notabilísima calidad. Incluso cuando se plantea un tratamiento serio del personaje, caso por ejemplo de un biopic, e independientemente de la calidad del producto final, rara vez el tratamiento de la actividad docente y/o investigadora ha sido llevado a cabo con solvencia y fidelidad. DivM.: Como profesor de matemáticas, en tu tarea diaria. ¿Crees que el libro puede resultar de algún interés para las clases? Si es así, ¿cómo podría emplearse y a qué niveles? J.L.L.F.: Más que el libro en sí –probablemente más cercano al ensayo que a un manual de fidelización de conceptos para el estudiante– entiendo como útil, desde el punto de vista de la docencia, la información contenida en escenas concretas de algunas películas, en los fragmentos de algunas novelas, o bien en una variedad de canciones, cuadros u obras de teatro, en algunos casos con un alto valor didáctico. Bien seleccionadas en función del tema a tratar o el concepto a ilustrar, constituyen sin duda un valiosísimo referente de cara al estudiante (pongamos que de enseñanza secundaria e incluso de primer curso universitario, por fijar un margen de niveles académicos) para rebajar el (¿irremediable?) lastre que acostumbra acompañar a las matemáticas en itinerarios docentes o currículos de cualquier índole, incluso en los de carácter científico. En este sentido debo y quiero destacar la labor desarrollada por este portal –y en particular a través de esta sección– para acercar la matemática a los placeres de la vida, entre los cuales hay que considerar indubitablemente el cine (si no, no es vida). DivM.: Lo que se te ocurra acerca del libro que quieras destacar. Cómo se puede adquirir. J.L.L.F.: Quisiera aprovechar la libertad que me otorga la pregunta para volver a agradecer a toda la gente que, siendo mucha y buena, ha estado pendiente siempre de las evoluciones del libro y que ha aportado ideas, consejos, correcciones, referencias, películas, matemáticas y entusiasmo. De momento la única manera de adquirirlo es a través del portal lulu.com, concretamente vía el siguiente enlace: Además, algunos contenidos son compartidos públicamente en la siguiente página de Facebook: https://facebook.com/pages/La-cuadratura-del-celuloide/393875163967454.
Las matemáticas en la obra de Dalí surgen a raíz del apasionamiento que despierta en él el texto De divina proportione del matemático renacentista fray Luca Pacioli,132 en el que se describen los cánones que rigen las proporciones del cuerpo humano. Obsesionado por el estudio de tales proporciones, el artista se hizo valer de la ayuda del matemático rumano Matila Ghyka133 para llevar a cabo unos cálculos que culminaron con la confección en 1948 de la obra Leda atómica. Pocos años más tarde, sobre el famoso lienzo de 1951 Cristo de San Juan de la Cruz, contaría el artista que organizó la figura triangular de Cristo crucificado bajo la sugestión de la imagen, acaecida en sueños, de una esfera contenida dentro de un triángulo. Cuando Dalí recuerda su etapa en la Residencia de Estudiantes de Madrid ya parecía apuntar cierta predilección por el rigor propio del pensamiento matemático:134 Paradójicamente, aunque yo estaba entonces en Madrid, sólo para hacer pintura cubista, esperaba de mis profesores la ciencia exacta del dibujo, el color y la perspectiva.
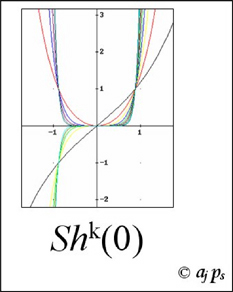
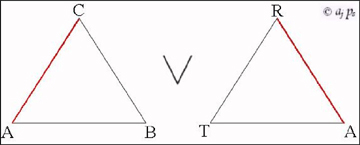
132.- Uno de los padres de la contabilidad y gran divulgador de la matemática euclidiana. 133.- Autor, entre otras obras, de Estética de las proporciones en la Naturaleza y en las Artes (1927) y El número de oro (1931). 134.- La vida secreta de Salvador Dalí, Vision Press. Londres, 1948. 135.- La relación de Dalí con el cine está descrita con detalle en el libro de Carlos Tejada Arte en fotogramas –Cine realizado por artistas, Ed. Cátedra, 2008. Como comentamos el mes pasado, Las Matemáticas en el Cine tiene una página en Facebook. Además de colocar de vez en cuando alguna noticia llamativa, informativa o de interés relacionada con estas dos disciplinas, se propone un juego (ya llevamos setenta y tantas películas) en el que a partir de una imagen con contenido matemático se trata de averiguar el título de la película que dichas expresiones o imágenes sugieren. Adjuntamos algunas de ellas, para que os comáis un ratillo el coco:
Como siempre, cualquier comentario, crítica o sugerencia puede hacerse a la dirección Esta dirección electrónica esta protegida contra spambots. Es necesario activar Javascript para visualizarla . |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |






 Desde que allá por el 2000, con motivo del Año Internacional de las Matemáticas, un servidor (hablo de mi, el que escribe esto, no una máquina que da servicio a una red de usuarios y clientes) empezara a recabar información sobre la relación entre las matemáticas y el cine (en ese momento apenas había en la Red una o dos entradas en inglés) se han venido multiplicando los lugares, blogs, y demás, que han tratado el asunto (lo cual está muy bien porque muchos ojos ven más que unos pocos). Sin embargo no es tan frecuente la aparición en el mercado editorial de libros que aborden desde un punto de vista más reflexivo esta relación (aunque haya quien piense lo contrario, en esto que ahora llamamos “nube” se escribe a bote pronto, precipitadamente, porque todo parece tener una inmediatez con fecha de caducidad, y por ello todo desaparece también rápidamente, mientras que quien se decide a escribir o editar un libro, algo más perdurable aparentemente, cuida más su trabajo, mide más las expresiones y las ideas, lo trabaja más en suma). Y mucho menos en nuestro país. Por eso, creo que es muy destacable que en poco tiempo hayan aparecido de golpe dos nuevas publicaciones sobre este tema: La cuadratura del celuloide (José Luís López Fernández, Abril, 2012, 526 páginas) y Math Goes to the Movies (Burkard Polster y Marty Ross, Johns Hopkins University Press, Septiembre, 2012, 304 páginas). Y también me parece adecuado dedicar a cada uno una reseña de esta sección. Comenzamos en esta ocasión con el primero de ellos.
Desde que allá por el 2000, con motivo del Año Internacional de las Matemáticas, un servidor (hablo de mi, el que escribe esto, no una máquina que da servicio a una red de usuarios y clientes) empezara a recabar información sobre la relación entre las matemáticas y el cine (en ese momento apenas había en la Red una o dos entradas en inglés) se han venido multiplicando los lugares, blogs, y demás, que han tratado el asunto (lo cual está muy bien porque muchos ojos ven más que unos pocos). Sin embargo no es tan frecuente la aparición en el mercado editorial de libros que aborden desde un punto de vista más reflexivo esta relación (aunque haya quien piense lo contrario, en esto que ahora llamamos “nube” se escribe a bote pronto, precipitadamente, porque todo parece tener una inmediatez con fecha de caducidad, y por ello todo desaparece también rápidamente, mientras que quien se decide a escribir o editar un libro, algo más perdurable aparentemente, cuida más su trabajo, mide más las expresiones y las ideas, lo trabaja más en suma). Y mucho menos en nuestro país. Por eso, creo que es muy destacable que en poco tiempo hayan aparecido de golpe dos nuevas publicaciones sobre este tema: La cuadratura del celuloide (José Luís López Fernández, Abril, 2012, 526 páginas) y Math Goes to the Movies (Burkard Polster y Marty Ross, Johns Hopkins University Press, Septiembre, 2012, 304 páginas). Y también me parece adecuado dedicar a cada uno una reseña de esta sección. Comenzamos en esta ocasión con el primero de ellos. A pesar del título, en el libro de David Thompson la mención de la palabra ecuación no es más que gramatical: según su punto de vista, la verdad sobre Hollywood se resume en "La ecuación completa", una fórmula integrada por dos factores que no pueden existir el uno sin el otro: el arte y el dinero. Esa es la excusa para hacer un repaso por la historia del cine norteamericano desde esa perspectiva, pero sin matemáticas explícitas por ninguna parte.
A pesar del título, en el libro de David Thompson la mención de la palabra ecuación no es más que gramatical: según su punto de vista, la verdad sobre Hollywood se resume en "La ecuación completa", una fórmula integrada por dos factores que no pueden existir el uno sin el otro: el arte y el dinero. Esa es la excusa para hacer un repaso por la historia del cine norteamericano desde esa perspectiva, pero sin matemáticas explícitas por ninguna parte. En penúltimo lugar nos encontramos con 0*2, El Amor (verso de Gabriel Celaya del poema Tablas de multiplicar, una visión propia e irónica de la tabla de multiplicar llena de metáforas: “cero por cero es la luz”, “cero por uno, el problema”, “cero por dos, el amor”. Gabriel Celaya estudió Ingeniería Industrial, aunque finalmente encaminó sus pasos por la poesía), capítulo dedicado a la relación entre la poesía y las matemáticas. Describiendo brevemente su amplio contenido, se recuerdan algunos matemáticos que han explorado esta relación, y descubrimos poetas para los que las matemáticas son una inutilidad, mientras que otros encuentran en ellas su fuente de inspiración. Se introduce la poesía científica y el grupo OULIPO (uno de cuyos integrantes más destacados es Raymond Queneau, en la foto) que utiliza estructuras matemáticas para la creación literaria. En este capítulo encontramos una pequeña errata matemática (creo que la única) en la página 394: eπi–1 = 0 (el signo debe ser +). Llama la atención una de las últimas reflexiones con las que finaliza el capítulo: “el lenguaje poético es sólo un disfraz del pensamiento matemático y de la puesta en escena cinematográfica”.
En penúltimo lugar nos encontramos con 0*2, El Amor (verso de Gabriel Celaya del poema Tablas de multiplicar, una visión propia e irónica de la tabla de multiplicar llena de metáforas: “cero por cero es la luz”, “cero por uno, el problema”, “cero por dos, el amor”. Gabriel Celaya estudió Ingeniería Industrial, aunque finalmente encaminó sus pasos por la poesía), capítulo dedicado a la relación entre la poesía y las matemáticas. Describiendo brevemente su amplio contenido, se recuerdan algunos matemáticos que han explorado esta relación, y descubrimos poetas para los que las matemáticas son una inutilidad, mientras que otros encuentran en ellas su fuente de inspiración. Se introduce la poesía científica y el grupo OULIPO (uno de cuyos integrantes más destacados es Raymond Queneau, en la foto) que utiliza estructuras matemáticas para la creación literaria. En este capítulo encontramos una pequeña errata matemática (creo que la única) en la página 394: eπi–1 = 0 (el signo debe ser +). Llama la atención una de las últimas reflexiones con las que finaliza el capítulo: “el lenguaje poético es sólo un disfraz del pensamiento matemático y de la puesta en escena cinematográfica”. Éstas consisten básicamente en alterar las estructuras espacio-temporales de la acción. A todos nos vienen a la cabeza, además de las citadas anteriormente de Tarantino, la exitosa trilogía de González Iñarritu Amores Perros, 21 Gramos y Babel, o Memento y Origen, de Christopher Nolan, o esa maravilla que constituyó el epitafio del veterano Sydney Lumet, Antes que el diablo sepa que has muerto (2007). Otro recurso relacionado, que ya tiene su solera, es la fragmentación de la pantalla en múltiples ventanas que nos muestran a la vez acciones que suceden en distintos lugares o en distintos planos del mismo lugar (la aparición del CinemaScope para luchar contra la competencia televisiva motivó este tipo de artificios). La reflexión final del capítulo, y por tanto del libro, es si la aparición de este cine no lineal tan de moda actualmente será el que caracterizará el cine de estos inicios del siglo XXI, un cine en el que el espectador no puede permanecer pasivo si quiere enterarse de algo, en definitiva, un cine para pensar.
Éstas consisten básicamente en alterar las estructuras espacio-temporales de la acción. A todos nos vienen a la cabeza, además de las citadas anteriormente de Tarantino, la exitosa trilogía de González Iñarritu Amores Perros, 21 Gramos y Babel, o Memento y Origen, de Christopher Nolan, o esa maravilla que constituyó el epitafio del veterano Sydney Lumet, Antes que el diablo sepa que has muerto (2007). Otro recurso relacionado, que ya tiene su solera, es la fragmentación de la pantalla en múltiples ventanas que nos muestran a la vez acciones que suceden en distintos lugares o en distintos planos del mismo lugar (la aparición del CinemaScope para luchar contra la competencia televisiva motivó este tipo de artificios). La reflexión final del capítulo, y por tanto del libro, es si la aparición de este cine no lineal tan de moda actualmente será el que caracterizará el cine de estos inicios del siglo XXI, un cine en el que el espectador no puede permanecer pasivo si quiere enterarse de algo, en definitiva, un cine para pensar. Reproducimos finalmente un párrafo del libro, a modo de muestra de su estilo y contenido (las imágenes han sido añadidas):
Reproducimos finalmente un párrafo del libro, a modo de muestra de su estilo y contenido (las imágenes han sido añadidas): En el ocaso de su carrera artística se mostró profundamente inquieto por la autoridad que la ciencia había demostrado ejercer en el sondeo de los misterios de la naturaleza, en particular por la teoría de catástrofes de René Thom -cuya simbología inspiró La cola de la golondrina– , la fisión atómica –a la que debe la idea de pintar figuras descompuestas en multitud de unidades elementales, como es el caso de Madonna de Port Lligat, Galatea de las esferas, Dalí desnudo en contemplación ante cinco cuerpos regulares o La Madona de Rafael a máxima velocidad–, el ADN –referido en La batalla de Tetuán–, la mecánica cuántica o la ecología.
En el ocaso de su carrera artística se mostró profundamente inquieto por la autoridad que la ciencia había demostrado ejercer en el sondeo de los misterios de la naturaleza, en particular por la teoría de catástrofes de René Thom -cuya simbología inspiró La cola de la golondrina– , la fisión atómica –a la que debe la idea de pintar figuras descompuestas en multitud de unidades elementales, como es el caso de Madonna de Port Lligat, Galatea de las esferas, Dalí desnudo en contemplación ante cinco cuerpos regulares o La Madona de Rafael a máxima velocidad–, el ADN –referido en La batalla de Tetuán–, la mecánica cuántica o la ecología. Dalí colaboró con su amigo Federico García Lorca en la obra teatral Mariana Pineda, para la que diseñó trajes y escenografía. En el terreno cinematográfico
Dalí colaboró con su amigo Federico García Lorca en la obra teatral Mariana Pineda, para la que diseñó trajes y escenografía. En el terreno cinematográfico