 96. Nuevo Año, Nuevos Propósitos
96. Nuevo Año, Nuevos Propósitos |
 |
 |
 |
| Escrito por Alfonso Jesús Población Sáez |
| Viernes 09 de Enero de 2015 |
|
Es habitual, finalizado un año, hacer un repaso de lo tratado, e intentar fijar nuevas metas para el nuevo. Empecemos en nuestro caso con una pequeña reflexión, que nos servirá para presentar un destacable documental e ir adelantando algo sobre la recién estrenada “Descifrando Enigma”. Las Matemáticas y el Cine. Desde que allá por 2005 comenzábamos estas reseñas mensuales, uno tiene la impresión de que sí que ha cambiado algo esta asociación, un tanto insólita en aquel momento. Entonces no eran muchos los que fueran capaces de indicar alguna relación entre esas disciplinas tan aparentemente alejadas; como mucho, encontrábamos media docena de títulos que más o menos tuvieran algún contenido o comentario de tipo matemático, casi siempre anecdótico o que el protagonista se dedicara por alguna peregrina razón a enseñar o trabajar con fórmulas y símbolos. Hoy, raro es el blog, revista de divulgación (incluso seria) y hasta programa de radio o televisión que no haga alguna referencia o apunte a las matemáticas (o la ciencia en general) y el cine. Hasta se han publicado algunos libros sobre el tema, que si bien no han llegado a ser súper-ventas (ni lo pretendían ni por asomo, por supuesto), sí han recibido una agradecida respuesta de lectores y puede que hayan contribuido a que editores, libreros, cineastas, y personas en general no dejen traslucir un semblante similar al de haber sido interpelados por alguien que vague por Betelgeuse como poco (aunque también ha contribuido la moda de ser freakie de lo que sea). Pero además de localizar títulos y referencias a las matemáticas, y en algún caso, proponer ejercicios relacionados con tal o cual escena o película concreta (es decir, una cierta motivación o enganche para algunos alumnos), ¿esto sirve para algo más allá de la anécdota? ¿Podemos afirmar que el cine puede ser un recurso a partir del que un profesor pueda enseñar matemáticas? La respuesta creemos que depende de cada uno, de su propia concepción de la materia, de cómo se plantee la enseñanza, de lo que esté dispuesto a “entretenerse” en preparar las clases, etc. Hay muchos docentes, afortunadamente cada vez más, que conciben la enseñanza de las matemáticas de un modo diferente al que hemos aguantado a través de los siglos (que no es que sea malo, ojo, la prueba es que algunos hemos adoptado las matemáticas como “nuestra” profesión, pero si que cada vez es menos atrayente para el alumno actual, que vive en un mundo muy diferente al del pasado, rodeado de estímulos visuales, digitales, tecnológicos), pero estaremos de acuerdo en que siguen siendo la minoría. Y qué demonios, ¿para que complicarse? El que no quiera estudiar ni aprender, es su problema. Los materiales manipulativos, juegos matemáticos, novelas, vídeos, hasta los problemas de olimpiadas matemáticas o recreativos, etc., todo son…. ¡Paparruchas! (está reciente Dickens y su Mr. Scrooge). Lápiz, papel, pizarra (de tiza, por supuesto) y libro de texto (¿porqué cada vez añaden más páginas con asuntos de historia de las matemáticas y problemas de los que los alumnos, y yo, docente, pasamos completamente? Claro, así el libro es más caro y las editoriales ganan más) son suficientes. Evidentemente con esta mentalidad, poco más hay que decir, salvo que quizá, amigo, la enseñanza en ese caso (no sólo de las matemáticas) no sea lo tuyo, al menos en la actualidad. ¡Ah, claro, es que el temario hay que acabarlo y cada vez hay menos tiempo! Es verdad, el recurrido asunto del temario. Evidentemente, si no me da tiempo tal y como lo hago actualmente, a lo mejor lo que hay que hacer es cambiar el método. ¡Ah, que no da tiempo a asimilar los conceptos si no hago tropecientos y pico mil ejercicios de patas, cabezas y gallinas! Claro, claro, siempre hay un pero. Pues añadamos otro: ¿pero no os habéis fijado que desde 1º ESO hasta 4º ESO se repiten (será para repasar, ¿no?) constantemente algunos temas? Ok, estupendo. El que escribe tiene la solución. Voy a escribirle y que me muestre su maravillosa panacea universal para tener a los alumnos atentos, interesados y que aprendan todos. Pues miren, no, lo siento. La solución homeopática aquí (ni en ningún lado, por cierto) existe. Cada curso, cada grupo, cada alumno, requiere diferentes “tratamientos”. Con estas líneas no pretendo dar solución alguna, sólo que pensemos en ello, siquiera los diez minutos que tardamos en leerlo, si es que llegamos al final. Esto sólo pretende ser una reflexión que me hago y comparto, que puede que no tenga ningún sentido (¡¡decídmelo, compartid vuestras opiniones!!). Hablando estrictamente de matemáticas, que independientemente de la metodología, supongo que eso al menos nos une a todos, hace 20 años, era impensable encontrar en el medio que fuera, a compañeros investigadores, profesores, españoles, publicando libros, hablando en la radio o en la televisión, proponiendo actividades en museos o en la misma calle. Y recalco, españoles. Sólo teníamos referencias de Gardner, Stewart, Bolt, etc. Y conste que a mi el orgullo patrio nacional, me importa más bien poco, pero sinceramente, uno se siente reconfortado porque (a lo mejor sólo es ilusión, pero quiero creer que no) con compañeros motivando las matemáticas, mostrando sus aplicaciones más allá de sus algoritmos técnicos en los que el más común de los mortales desconecta al primer “dado un épsilon positivo”, podemos pensar que nuestras aulas están mejor atendidas, aunque sólo sea para comentar aquello que se dijo en Órbita Laika anoche. Pero no nos engañemos. Siendo positivo, aunque sólo sea un épsilon insignificante, no bastaría con que fuera flor de un día. Muchos países (y no pensemos que sólo los más desarrollados que el nuestro, porque podemos encontrar sorpresas, sonrojantes para nosotros) nos llevan mucha ventaja en este sentido. Pero en fin, ahí estamos, al menos, de momento. Volviendo a nuestro redil, sería fácil argumentar aquello de que los medios audiovisuales son actualmente imprescindibles para demostrar que existes (en positivo también; en negativo supongo que todo el mundo sabe que gobiernos y dirigentes tratan siempre de controlar estos medios. Recordemos Goebbles y Leni Riefenstahl, por ejemplo, y sí, ya sé que no debo irme tan lejos en el tiempo para poner el ejemplo). Desde esta sección hemos venido alternando las películas comerciales con los documentales de temática matemática y los programas de televisión. Y siempre nos hemos venido lamentando de la poca incidencia que nuestros matemáticos (y científicos, en general) tienen. No obstante la comunidad matemática está haciendo notables esfuerzos en este sentido (asociaciones, profesores, investigadores, como dije antes). Sirvan estas líneas para apoyar su labor, y pedirles que continúen en esa línea, porque con el paso del tiempo, los documentos filmados seguirán estando, y los alumnos, las personas en general, podrán engancharse con más facilidad al estudio de la obra de los científicos (por supuesto después deberán pasar a las fuentes tradicionales si desean profundizar) o de cualquier personaje notable de cualquier rama del conocimiento y la cultura. Y como todo se entiende mejor con algún ejemplo concreto, en esta ocasión vamos a acercarnos a un reciente documental producido por el Instituto Henri Poincaré con motivo del bicentenario del fallecimiento en 2013 de Joseph-Louis Lagrange (1736 – 1813), en coproducción con el CNRS (Centre Nationale de la Recherche Scientifique) y el Instituto Lagrange de París. Recientemente se ha puesto a disposición de todos este documental en la red (más adelante se indica el enlace) y por ello me ha parecido interesante compartirlo y que, de paso, valoréis si merece o no la pena realizar y divulgar este tipo de documentos.
Previamente una pequeña ficha técnica. Título Original: Lagrange. Nacionalidad: Francia, 2013. Dirección: Quentin Lazzarotto. Dirección Científica: Frederic Brechenmacher. Animación Gráfica: Arthur Milleville. Música: Arthur Dairaine Andrianaivo. Producción: Cédric Villani, Jean-Philippe Uzan para el Henri Poincaré Institute (IHP), en coproducción con CNRS Images y el Instituto Lagrange de Paris. La película ha recibido financiación de la Universidad Pierre y Marie Curie, y de Labex Carmin. Duración: 33 min. Colaboradores: Luigi Pepe (Universidad de estudios de Ferrara), Jérôme Pérez (Profesor del ENSTA Paristech), Silvia Roero (Universidad de estudios de Torino), Cédric Villani (Universidad de Lyon, Director del Instituto Henri Poincaré), Bruno Belhoste (Universidad Paris 1), Alberto Conte (Presidente de la Academia de Ciencias de Turín), Laurent Guin (Estudiante de tercer año en L’Ecole Politechnique), Eberhard Knobloch (Miembro de la Academia de las Ciencias de Berlín-Brandenburgo), Jacques Laskar (CNRS, Observatorio de París, Miembro del Bureau de las longitudes, entre otros cargos), Thomas Morel (Universidad Técnica de Berlín), Anne-Sophie Bonnet-Bendhia, Jenny Boucard, Maria Munoz. El documental sigue un esquema clásico de localización de lugares que marcan la vida y la obra del personaje según se desgrana su biografía, salpicado por intervenciones de prestigiosas personalidades que lo han estudiado y/o trabajado. Antes del título, algunos de ellos nos hacen, en pocas palabras, una semblanza de lo que destacarían de Lagrange: unos destacando su trabajo matemático, otros en Física, Astronomía, en su trabajo académico, y algunos nos adelantan detalles de su personalidad. Tras ese preámbulo, visitaremos las tres ciudades que marcaron con mayor incidencia su existencia: Turín, Berlín y París.
Como el documental puede verse íntegro (en francés; no obstante en este enlace además se puede ver subtitulado en inglés), no me parece oportuno detallarlo al completo, simplemente destacar algunas curiosidades como que Lagrange, a diferencia de otros que trabajaron como filósofos, físicos u otras disciplinas, siempre lo haría como matemático; que le disgustaban profundamente las visitas y la vida social; que siempre trabajaba sin descanso alguno de 6 de la tarde a 12 de la noche; que la Revolución francesa le pilló en mal momento y por supuesto que su producción científica es de las más destacables de la Historia. Personalmente no conocía los denominados puntos de Lagrange. Están muy relacionados con un problema clásico que abordó Lagrange: el problema de los tres cuerpos. Todos hemos estudiado que la atracción gravitatoria que un cuerpo ejerce sobre otro de distinta masa es directamente proporcional al producto de dichas masas, e inversamente proporcional al cuadrado de la distancia que los separa. Incluso podemos sin demasiada dificultad escribir la fórmula que sintetiza dicha ley, universalmente conocida como ley de gravitación universal, y que fue expuesta por Isaac Newton. Con dos cuerpos por tanto, la cosa está bastante clara. Sin embargo las cosas se complican, y mucho, cuando entran en escena tres o más cuerpos. De hecho, hoy conocemos que la dinámica de tres cuerpos es caótica, tan irregular que presenta indicios de aleatoriedad. Hasta finales del siglo XIX, poco se sabía sobre el movimiento de tres cuerpos celestes, aunque uno de ellos fuera de una masa poco menos que despreciable. Volviendo a la reflexión con la que empezaba, una vez producido y realizado el documental, ¿de qué serviría si no se difunde? Pero no sólo comercializándolo o poniéndolo a disposición de todos. El 6 de Diciembre de 2013, uno de los colaboradores del documental, Jérôme Perez, astrofísico teórico del Laboratoire de Mathématiques Appliquées del ENSTA Paristech, organiza un auténtico maratón acerca de Lagrange, uno de cuyos elementos lo constituye el visionado del documental. Quien desee ver todas las conferencias y actos en relación con esta celebración (en francés), puede acceder a través de este enlace. Descifrando Enigma
Tenemos en la actualidad también esta película, comercial en este caso, acerca de la vida y parte de la obra de Alan Turing, producción que además opta a cinco globos de oro. A través de la página de Facebook de Las Matemáticas en el Cine, se han ido incorporando algunas de las críticas y reseñas que algunos medios de comunicación han venido realizando sobre la película. Aquí haremos un análisis un poco más profundo de la misma, aunque cabe adelantar que se trata de un producto interesante, mucho menos tramposo que la recreación de la vida de Nash en Una mente maravillosa, aunque no le falte en determinados momentos esa exagerada tensión que trata de hacerla más comercial, aún distorsionando ciertos aspectos por los que no es de extrañar que el biógrafo oficial, Andrew Hodges, en cuya detallada obra se ha basado el guionista, haya puesto el grito en el cielo. Sutilezas aparte, uno de sus grandes aciertos es que transmite con cierta emoción al público en general, una de las aplicaciones prácticas más palpables de las matemáticas que además ha sido rigurosamente cierta. Algo tangible. Tangible pero, no olvidemos, generado por todos esos símbolos, ecuaciones y teoremas que la gente considera aún más indescifrables que el propio código Enigma. Muy recomendable para los que aún no la hayan visto. Los peros, el próximo mes. |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |






 Pues a pesar de eso, si tomamos los ejercicios que se proponían de cualquier tema hace unos años de un libro como el de la foto (lo he comprobado con alumnos que obtienen buenas calificaciones de 3º y 4º de la ESO) por poner con el que un servidor estudió, pues, en fin, que andan un poco perdidos y que maldicen su existencia (y la mía).
Pues a pesar de eso, si tomamos los ejercicios que se proponían de cualquier tema hace unos años de un libro como el de la foto (lo he comprobado con alumnos que obtienen buenas calificaciones de 3º y 4º de la ESO) por poner con el que un servidor estudió, pues, en fin, que andan un poco perdidos y que maldicen su existencia (y la mía).
 En Turín, el matemático y actualmente Presidente de la Sociedad Italiana de Historia de las Matemáticas, Luigi Pepe aparece recorriendo la Via Lagrange en busca del portal nº 29, edificio donde nació Lagrange. ¿A que pensabais que era francés? Pues no, piamontés, de nombre Giuseppe Luigi Lagrange, como se muestra en una lápida de la casa natal. De paso se nos va contando cómo su padre fue tesorero público del Estado y su madre hija de un rico doctor de Cambiano, que tuvieron once hijos, siendo nuestro Lagrange el primogénito. A los 14 años ingresó en la Universidad de Turín donde estudió durante dos años entre otros el Introductio in analysin infinitorum (Euler, 1748) (para muchos “el libro de texto más importante de los tiempos modernos”), el tratado de Wolff, el libro de Agnesi o el de cálculo integral de Johann Bernoulli, entre otros. Después trabajó como colaborador ayudante de los profesores de matemáticas en la Academia Militar de Turín, dando clase a personas siempre mayores que él.
En Turín, el matemático y actualmente Presidente de la Sociedad Italiana de Historia de las Matemáticas, Luigi Pepe aparece recorriendo la Via Lagrange en busca del portal nº 29, edificio donde nació Lagrange. ¿A que pensabais que era francés? Pues no, piamontés, de nombre Giuseppe Luigi Lagrange, como se muestra en una lápida de la casa natal. De paso se nos va contando cómo su padre fue tesorero público del Estado y su madre hija de un rico doctor de Cambiano, que tuvieron once hijos, siendo nuestro Lagrange el primogénito. A los 14 años ingresó en la Universidad de Turín donde estudió durante dos años entre otros el Introductio in analysin infinitorum (Euler, 1748) (para muchos “el libro de texto más importante de los tiempos modernos”), el tratado de Wolff, el libro de Agnesi o el de cálculo integral de Johann Bernoulli, entre otros. Después trabajó como colaborador ayudante de los profesores de matemáticas en la Academia Militar de Turín, dando clase a personas siempre mayores que él.

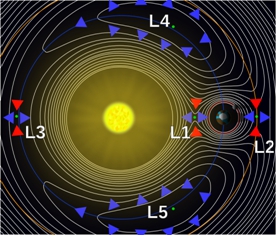 Lagrange estudió lo que se denomina el problema restringido, es decir, considerando que las órbitas fueran o bien circulares o bien elípticas. En el caso circular, se demostró la existencia de cinco puntos de equilibrio, los puntos de Lagrange, denominados así en su honor. En la imagen (tomada de la Wikipedia) aparecen detallados esos puntos y sus curvas de potencial (sólo aparecen dos cuerpos, el Sol y la Tierra). Quien desee profundizar un poco (nivel elemental) sobre el asunto, una vez visinado el documental, puede consultar la entrada de donde se ha tomado la imagen,
Lagrange estudió lo que se denomina el problema restringido, es decir, considerando que las órbitas fueran o bien circulares o bien elípticas. En el caso circular, se demostró la existencia de cinco puntos de equilibrio, los puntos de Lagrange, denominados así en su honor. En la imagen (tomada de la Wikipedia) aparecen detallados esos puntos y sus curvas de potencial (sólo aparecen dos cuerpos, el Sol y la Tierra). Quien desee profundizar un poco (nivel elemental) sobre el asunto, una vez visinado el documental, puede consultar la entrada de donde se ha tomado la imagen, 