 108. OBELISKOS
108. OBELISKOS |
 |
 |
 |
| Escrito por Alfonso Jesús Población Sáez |
| Lunes 07 de Marzo de 2016 |
|
Se acerca la Semana Santa, y las televisiones (¡¡gran imaginación!!) suelen programar películas de corte bíblico o histórico. Y con sus limitaciones argumentales (la época de producción es la que es), normalmente las clásicas siguen siendo la mejor opción. Y en algunas, hasta podemos encontrar algo de matemáticas...
Prescindiremos en esta ocasión de la ficha técnica y artística, dado que sólo nos vamos a referir a una escena concreta, y no a la película íntegra. Todo un clásico: Los diez mandamientos, (The Ten Commandments, EE. UU., 1956), de Cecil B. de Mille. ¿Qué matemáticas podemos encontrar en ella aparte del número del título? Pensemos medio minuto.... Vaya el título de la reseña, lo delata. Durante el primer cuarto de la película, Moisés (Charlton Heston), hijo adoptado por el faraón Seti (Cedric Hardwicke) (supongo que todo el mundo conoce aquello de que fue salvado de las aguas por la hija del faraón que no podía tener descendencia), resulta ser un competente ingeniero al que Seti encarga erigir en su nombre toda una ciudad, ante la indolencia del hijo legítimo del faraón, Ramsés (Yul Brynner). Uno de los momentos más delicados de la construcción es el levantamiento de los enormes obeliscos que anuncian la entrada a la ciudad. En ese instante, inoportunamente, se presenta el faraón que se molesta por parecer no ser bien recibido. Esta es la escena (que puede verse aquí; desde el minuto 0:53): Baka: Esa pendiente exige más presión para levantarla. Hace falta más arena. Moisés: Yo voy a arriesgarme. Queda poco tiempo para el día del aniversario. Baka: Y si la piedra se parte, nos partimos con ella. Moisés: ¿Preparado el sistema de señales? ¡Flámula Azul! Capataz: ¡Flámula azul! ¡Quitad los calzos! Señalero: Calzos quitados. Moisés: ¡Flámula verde! Capataz 2: ¡Los maceros! ¡Preparados! Señalero: Maceros a punto.
Seti: ¿No te complace verme aquí? Moisés: Mucho, Gran Faraón. Pero ahora tengo algo muy importante que hacer. ¡Preparada flámula roja! Seti: Sí, ya me lo había dicho Ramsés. ¿Y es más importante que obedecer mis órdenes? Moisés: Tú me ordenaste que terminara esta ciudad. La tensión desafiada es enorme. No podemos esperar. ¡Flámula roja! Capataz 2: ¡Flámula roja! ¡Descargad! El obelisco va elevándose. Producto de la tensión se van rompiendo a trozos la plataforma de madera sobre la que descansa. La fuerza hace que varios obreros (esclavos, en este caso) que sujetan las cuerdas para que el obelisco siga una trayectoria y no se vaya a un lado, sean despedidos por el aire. Setí: ¡Se quebrará! Moisés: Hay 2000 esclavos en las maromas. El obelisco se acaba poniendo en pie con gran expectación de todos.
Moisés: ¿Satisfecho el faraón? Seti: Del obelisco, sí, pero no de ciertas acusaciones que se han hecho contra ti... Hasta aquí lo relativo al obelisco (la escena puede seguirse hasta el final en el enlace anterior). Digamos sobre el diálogo que, está bastante bien doblado respecto a la versión original. Es ligeramente diferente la primera frase de Baka que en el original dice “Esa caída pone demasiada tensión en la piedra. Necesitamos más arena”, que bajo mi punto de vista es más correcta. Para levantar el obelisco la pendiente no exige más presión, en todo caso exige más fuerza, pero no se entiende lo de “presión”. En cambio, en la versión original, que la pendiente ponga mucha tensión para levantar el citado obelisco, sí es correcto. En cualquier caso, esta superficie tridimensional parece “confundir” a mucha gente, porque a lo largo de la Historia ha sido objeto de múltiples atenciones y desplantes. Para empezar, si buscamos en el diccionario de la Real Academia Española de la Lengua su definición, nos encontramos con lo siguiente: Del lat. obeliscus, y este del gr. ὀβελίσκος obelískos, dim. de ὀβελός obelós 'espeto', usado en sent. irón. 1. m. Pilar muy alto, de cuatro caras iguales un poco convergentes y terminado por una punta piramidal muy achatada, que sirve de adorno en lugares públicos. 2. m. Señal que se solía poner en el margen de los libros para anotar una cosa particular. Creo que no hace falta tampoco comentar demasiado con términos como “muy alto”, “un poco”, “muy achatada”. Vamos, una definición “súper-precisa”, con la que alguien que no haya visto nunca uno le queda claro el concepto. Tampoco en algunas páginas de internet dedicadas en teoría a aclarar dudas, se quedan atrás. En alguna se puede leer “poliedro que se obtiene al truncar un cuña con un plano paralelo a la base”. ¿Qué pasa que las “cuñas” son estándar? Porque yo puedo imaginar muchas cuñas (entendiendo por cuña lo que entiende todo el mundo) diferentes que desde luego no proporcionan obeliscos al cortarlas por un plano de esos. Sinceramente, da la impresión de que este tipo de definiciones son a posteriori de conocer qué es un obelisco, y sencillamente tratan de describirlo lo más aproximadamente que saben con pocas palabras. Y eso en matemáticas sabemos que no vale. El diccionario británico lo hace “algo” (el entrecomillado es sarcástico) mejor: Pilar de piedra de sección transversal cuadrada o rectangular y caras laterales que se estrechan hacia una parte superior piramidal, que a menudo se utilizó como monumento en el antiguo Egipto.
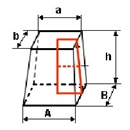
El problema de la erección Que nadie piense mal cuando lea el título del párrafo, estamos hablando de obeliscos. Quizá por ello, desde la misma cultura egipcia, se lo ha relacionado también con el poder, con la forma fálica, porque ese órgano, justificaban, proporciona vida. Quizá también por eso, el uso de la palabra obelisco (entendiendo en este contexto por tal el egipcio) estaba prohibido en la Biblia, y fue sustituida por “imágenes”. Por ejemplo, en Éxodo 34:13, se dice, “Derribaréis sus altares, y quebraréis sus estatuas, y cortaréis sus imágenes de Asera”. No podemos asegurar cuando realmente se refiere a imágenes o a obeliscos (la seudociencia iluminada ha ido emborronándolo todo a lo largo de los siglos lamentablemente), el caso es que el hecho objetivo es que la palabra obelisco no aparece en la Biblia, al menos en la oficial. Se le de la interpretación que se quiera, el caso es que muchas naciones, también en la actualidad, han erigido obeliscos para conmemorar victorias. Y muchas de las grandes urbes actuales (incluido en el Vaticano, paradójicamente; el que quiera puede curiosear un poco aquí por los trece obeliscos de Roma, porque es curioso en muchos casos) tienen alguno (lamentablemente la mayor parte expoliados a Egipto). A lo que íbamos. Trasladar un obelisco o levantarlo conlleva muchos problemas técnicos, dada su imponente altura, y a que estaban tallados, como ya se ha dicho, de una sola pieza. Añadiendo a ello el material, normalmente la piedra, que los hacen muy pesados. Así pues la escena de la película no es en absoluto trivial. Incluso hoy en día los problemas que ha habido que solventar han sido cuantiosos, lo que ha alimentado (¡Otra vez! Están por todos los lados) teorías de lo más variopinto (no voy a repetir ninguna, pero os podéis imaginar a qué extremo llegan algunas) sobre cómo se solventó en la Antigüedad el problema de su erección. Es muy conocido, y más que aclarar, ha dado lugar a más especulaciones, el intento de levantar hace unos años un obelisco por un equipo de televisión capitaneado por Evan Hadingham, que posteriormente ha escrito varios artículos sobre el tema. Recientemente, la doctora Maureen Clemmons ha desarrollado, con cierto éxito, el proyecto Cometa, en el que gracias a la fuerza del viento, y a un sistema de cometas, ha logrado izar pesos de cierta envergadura. Mayor información y vídeos en este enlace. Volumen de un obelisco A todo esto, ¿sabrías calcular el volumen de un obelisco? Se trata de calcular el volumen del obelisco de la figura (le hemos quitado el piramidón de la parte superior; simplemente se le sumaría a lo que vamos a calcular), de altura h y de bases rectangulares de dimensiones A, B, para la base mayor, y a, b, para la menor. El volumen lo calculamos, por ejemplo, por secciones, perpendiculares al eje OZ (el vertical, cuyos límites para el obelisco señalado serán entre 0 y h). ¿Por qué? Pues es evidente: las secciones son rectángulos, y otra cosa no sabremos, pero el área de un rectángulo, si, base por altura. Así pues, si pasáramos una cuchilla por el obelisco a altura z y perpendicularmente al eje Z, obtendríamos el rectángulo marcado en verde de la imagen. El volumen del obelisco, vendrá entonces dado por la integral V = siendo S(z) la superficie del rectángulo pintado de verde. Todo el problema consiste en calcular ese área S(z) en función de los datos suministrados por el problema, es decir, A, B, a, b, y por supuesto z, que va a ser la variable de integración, y en donde va variando el corte que damos al objeto (entre 0 y h), porque el volumen vendrá dado por la suma de la áreas de los infinitos rectángulos que vamos obteniendo al pasar la “cuchilla” (en matemáticas somos menos agresivos, y decimos el plano) desde la base (z = 0) hasta la cúspide (z = h). El planteamiento es bastante claro (lo entiendo hasta yo mismo); otra cosa es que sepamos encontrar S(z), y luego resolver la integral (aunque en este caso será polinómica, o sea que la hace hasta un chaval de secundaria). Hagamos otro par de dibujillos para entender bien cómo vamos a razonar. Fijémonos en la superficie cuyos bordes están marcados en rojo en la imagen adjunta. Se trata de un trapecio que vamos a prolongar hasta la punta a un triángulo. En definitiva que vamos a pensar sobre el triángulo de esta nueva figura que tenemos dibujada por aquí.
Echando cuentas por separado en las igualdades, tomando respectivamente, primer y segundo miembro, y después el primero y el tercero, se llega sin demasiados esfuerzos a que
Operando en la primera, se tiene que BASE = Combinando ambas (o sea, sustituyendo la segunda en la primera), se obtiene que
Esa es la base del rectángulo que surge a la altura z. Necesitamos calcular la longitud del otro lado del rectángulo (o sea, exactamente las mismas cuentas pero con B y b). Se obtiene entonces que la altura del rectángulo “verde” viene dada por
¿Cuál es entonces S(z), área del rectángulo verde? Claramente, BASE por ALTURA.
Por tanto
Evidentemente las cuentas intermedias no están detalladas pero son elementales, pero si alguien tiene algún problema y está interesado, no tiene más que mandarme un correo. A todo esto, y ya puestos, el lector podría intentar deducir al área lateral y total de dicho obelisco, para completar su estudio, y tenerlo completamente dominado.
También a Ramsés (Yul Brynner) le da por juguetear con una balanza, para demostrar “las malas artes” de Moisés, sólo que éste parece que tiene respuestas más ingeniosas (¿Para qué necesitaba entonces a Aaron como intérprete ante el faraón? Charlton Heston se basta y sobra. Un par de curiosidades finales. El señor de la izquierda debe su nombre a los obeliscos también. Y este objeto fue elegido como símbolo de la masonería (también pirámides y triángulos), por lo que no es raro encontrarnos en muchos cementerios de nuestro país, tumbas y panteones coronados por estas figuras en lugar de cruces cristianas o con ellas en algún lateral, como el de la foto tomada en el cementerio del Carmen de Valladolid. ¿Quien nos iba a decir que estas superficies nos iban a dar tanto juego? |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |






 En ese momento, se presenta el faraón Seti acompañado de su hijo Ramsés. Moisés lo advierte y se quita un guante contrariado; los demás reverencian al faraón.
En ese momento, se presenta el faraón Seti acompañado de su hijo Ramsés. Moisés lo advierte y se quita un guante contrariado; los demás reverencian al faraón. Moisés: Ahí tienes el obelisco de tu aniversario. Baka, que un millar de esclavos retiren la arena para que el obelisco quede bien asentado en su base.
Moisés: Ahí tienes el obelisco de tu aniversario. Baka, que un millar de esclavos retiren la arena para que el obelisco quede bien asentado en su base.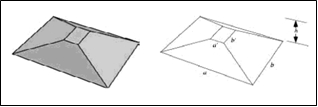 Si acudimos finalmente a la CRC Concise Encyclopedia of Mathematics, nos dice que es un “poliedro formado por dos rectángulos paralelos, no congruentes entre sí, cuyas caras laterales son trapecios”. Y acompañando la definición aparece la imagen de la derecha. ¡¡¡Bien!!! Por fin sabemos lo que es un obelisco. La pirámide que, en efecto los egipcios añadían en la parte superior, no es parte de la definición geométrica de obelisco. Era una pirámide de base el rectángulo superior del obelisco, pero cambiaba la pendiente que los trapecios llevaban desde la base. Se llama piramidión, y el colocarla tenía que ver con su concepción simbólica de los rayos del Sol (para los egipcios, el Sol era el que otorga vida). Por otro lado el obelisco también representa la estabilidad. Ellos tallaban el conjunto en una sola pieza, pero en realidad, matemáticamente, son dos objetos diferentes, un tronco de pirámide y otra pirámide, que, digámoslo de nuevo, cambia la pendiente de las aristas al llegar al piramidión. Para el acervo popular, el obelisco es identificado con el obelisco egipcio, pero como vemos, no es lo mismo.
Si acudimos finalmente a la CRC Concise Encyclopedia of Mathematics, nos dice que es un “poliedro formado por dos rectángulos paralelos, no congruentes entre sí, cuyas caras laterales son trapecios”. Y acompañando la definición aparece la imagen de la derecha. ¡¡¡Bien!!! Por fin sabemos lo que es un obelisco. La pirámide que, en efecto los egipcios añadían en la parte superior, no es parte de la definición geométrica de obelisco. Era una pirámide de base el rectángulo superior del obelisco, pero cambiaba la pendiente que los trapecios llevaban desde la base. Se llama piramidión, y el colocarla tenía que ver con su concepción simbólica de los rayos del Sol (para los egipcios, el Sol era el que otorga vida). Por otro lado el obelisco también representa la estabilidad. Ellos tallaban el conjunto en una sola pieza, pero en realidad, matemáticamente, son dos objetos diferentes, un tronco de pirámide y otra pirámide, que, digámoslo de nuevo, cambia la pendiente de las aristas al llegar al piramidión. Para el acervo popular, el obelisco es identificado con el obelisco egipcio, pero como vemos, no es lo mismo.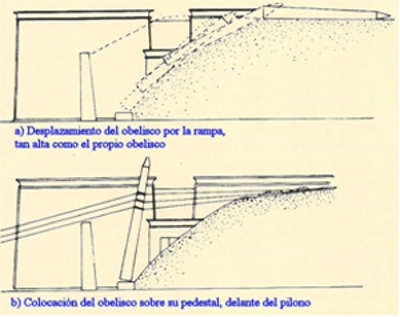 La más común, entre las no alucinadas, la que siguen explicando los guías turísticos in situ, es la mostrada en la película: se arrastra el obelisco hasta donde se quiere erigir haciéndolo descender a través de una rampa sobre la que se va deslizando hasta que coincidiera el borde inferior del obelisco con la muesca de la base del pedestal. Se iría controlando ese descenso mediante cuerdas haciendo uso de andamios, poleas, etc. Este sistema plantea múltiples interrogantes (no olvidemos que la mayor parte miden más de 30 metros de altura, pesan más de trescientas toneladas, y en muchos casos el espacio disponible alrededor era limitado a una veintena de metros). Algunos estudiosos indican un sistema de canales rellenos de arena que van dejando que el obelisco vaya cayendo en el espacio que la arena libera (recuérdese el sellado de la pirámide de la película Tierra de Faraones (Land of the Pharaohs, Howard Hawks, EE. UU., 1955)). La imagen está tomada de
La más común, entre las no alucinadas, la que siguen explicando los guías turísticos in situ, es la mostrada en la película: se arrastra el obelisco hasta donde se quiere erigir haciéndolo descender a través de una rampa sobre la que se va deslizando hasta que coincidiera el borde inferior del obelisco con la muesca de la base del pedestal. Se iría controlando ese descenso mediante cuerdas haciendo uso de andamios, poleas, etc. Este sistema plantea múltiples interrogantes (no olvidemos que la mayor parte miden más de 30 metros de altura, pesan más de trescientas toneladas, y en muchos casos el espacio disponible alrededor era limitado a una veintena de metros). Algunos estudiosos indican un sistema de canales rellenos de arena que van dejando que el obelisco vaya cayendo en el espacio que la arena libera (recuérdese el sellado de la pirámide de la película Tierra de Faraones (Land of the Pharaohs, Howard Hawks, EE. UU., 1955)). La imagen está tomada de 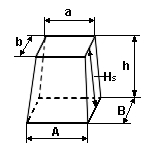 Se trata de un típico ejercicio propuesto en primeros cursos de carreras universitarias (ingenierías, etc.) como aplicación del cálculo de volúmenes mediante integrales definidas, pero así como no hay demasiados problemas para calcular el volumen de una pirámide o de un cono (bueno, miento, el 70% de los alumnos no lo hace o lo hace mal, incluso con esos cuerpos geométricos) con el obelisco parece que hay algo atávico (¡mira que si los vendedores de humo tuvieran razón! Pero en fin, yo les sugeriría que antes de hablar de propiedades supuestamente “mágicas”, al menos conocieran bien el objeto, y supieran por tanto cómo se hallan sus dimensiones básicas. Así podrían buscar cuerpos en proporción áurea, y todas esas cosas que tanto les gustan, y que en realidad, sólo son curiosidades y entretenimientos).
Se trata de un típico ejercicio propuesto en primeros cursos de carreras universitarias (ingenierías, etc.) como aplicación del cálculo de volúmenes mediante integrales definidas, pero así como no hay demasiados problemas para calcular el volumen de una pirámide o de un cono (bueno, miento, el 70% de los alumnos no lo hace o lo hace mal, incluso con esos cuerpos geométricos) con el obelisco parece que hay algo atávico (¡mira que si los vendedores de humo tuvieran razón! Pero en fin, yo les sugeriría que antes de hablar de propiedades supuestamente “mágicas”, al menos conocieran bien el objeto, y supieran por tanto cómo se hallan sus dimensiones básicas. Así podrían buscar cuerpos en proporción áurea, y todas esas cosas que tanto les gustan, y que en realidad, sólo son curiosidades y entretenimientos).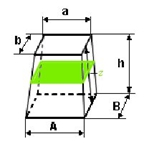
 ¿Por qué? Porque para relacionar los lados del rectángulo que nos sale a la altura z con las dimensiones del rectángulo base, y el de la “cima”, vamos a aplicar otro viejo conocido de la afición estudiantil, el teorema de Tales, y ése se aplica a triángulos.
¿Por qué? Porque para relacionar los lados del rectángulo que nos sale a la altura z con las dimensiones del rectángulo base, y el de la “cima”, vamos a aplicar otro viejo conocido de la afición estudiantil, el teorema de Tales, y ése se aplica a triángulos.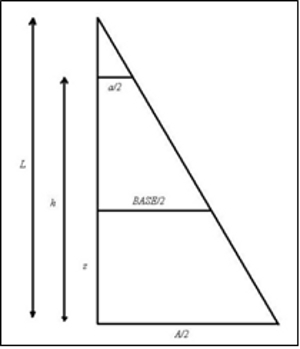 La base de dicho triángulo es A/2 porque la base del trapecio va desde el centro del rectángulo base al centro del lado, igualmente con el superior, a/2, y con el que está a altura z, que desconocemos, y lo hemos denotado como BASE/2. La altura total del triángulo la hemos llamado L, y h y z están señaladas claramente en el dibujo. Empecemos a aplicar Tales a los tres triángulos que aparecen:
La base de dicho triángulo es A/2 porque la base del trapecio va desde el centro del rectángulo base al centro del lado, igualmente con el superior, a/2, y con el que está a altura z, que desconocemos, y lo hemos denotado como BASE/2. La altura total del triángulo la hemos llamado L, y h y z están señaladas claramente en el dibujo. Empecemos a aplicar Tales a los tres triángulos que aparecen: Volviendo a la película, en la imagen adjunta observamos cómo el ingeniero Moisés maneja una especie de teodolito. Y lo llamo así, porque lo maneja y usa como un teodolito. Este instrumento de medición se utiliza para obtener ángulos verticales y, en la mayoría de los casos, horizontales, pues su precisión en éstos últimos es bastante ajustada. También pueden medirse con él distancias y desniveles, aunque en estos casos, con materiales auxiliares. Su fin es más bien topográfico (triangulaciones sobre todo). Moisés parece utilizarlo para medir distancias y ángulos, y a partir de esas mediciones, ordena a sus capataces (¡que bonita la palabra “flámula”, apenas utilizada!
Volviendo a la película, en la imagen adjunta observamos cómo el ingeniero Moisés maneja una especie de teodolito. Y lo llamo así, porque lo maneja y usa como un teodolito. Este instrumento de medición se utiliza para obtener ángulos verticales y, en la mayoría de los casos, horizontales, pues su precisión en éstos últimos es bastante ajustada. También pueden medirse con él distancias y desniveles, aunque en estos casos, con materiales auxiliares. Su fin es más bien topográfico (triangulaciones sobre todo). Moisés parece utilizarlo para medir distancias y ángulos, y a partir de esas mediciones, ordena a sus capataces (¡que bonita la palabra “flámula”, apenas utilizada!  Es, por cierto, una planta de olor muy agradable, pero extremadamente tóxica, con hojas en forma triangular, como las banderas utilizadas, muy vistosa, y parecida al almendro en flor o al jazmín). En el cine se han empleado en varias ocasiones.
Es, por cierto, una planta de olor muy agradable, pero extremadamente tóxica, con hojas en forma triangular, como las banderas utilizadas, muy vistosa, y parecida al almendro en flor o al jazmín). En el cine se han empleado en varias ocasiones.  Recordemos cómo Indiana Jones buscaba el lugar donde se escondía un objeto muy preciado (foto) en En busca del arca perdida (Steven Spielberg, EE. UU., 1981), o Hugh Grant trata de dilucidar si Ffinnon Garw es una colina o una montaña en El Inglés que subió una colina pero bajó una montaña (Christopher Monger, Gran Bretaña, 1995). En estos casos pase, pero ¿había teodolitos en el Antiguo Egipto? Si alguien lo sabe, que nos ilumine.
Recordemos cómo Indiana Jones buscaba el lugar donde se escondía un objeto muy preciado (foto) en En busca del arca perdida (Steven Spielberg, EE. UU., 1981), o Hugh Grant trata de dilucidar si Ffinnon Garw es una colina o una montaña en El Inglés que subió una colina pero bajó una montaña (Christopher Monger, Gran Bretaña, 1995). En estos casos pase, pero ¿había teodolitos en el Antiguo Egipto? Si alguien lo sabe, que nos ilumine.

 No sé, algo no me cuadra, pero en fin, esto es cine, y no debemos darle muchas vueltas).
No sé, algo no me cuadra, pero en fin, esto es cine, y no debemos darle muchas vueltas).