75. (Abril 2016) Consenso entre expertos en música: un enfoque matemático
75. (Abril 2016) Consenso entre expertos en música: un enfoque matemático |
 |
 |
 |
| Escrito por Paco Gómez Martín (Universidad Politécnica de Madrid) |
| Viernes 15 de Abril de 2016 |
|
1. Sobre el consenso entre expertos en música El artículo de este mes versa sobre un problema que me he encontrado con cierta frecuencia en el campo de la teoría musical y de la musicología. Ese problema es el del consenso entre expertos en música. A la hora de evaluar un fenómeno musical, ¿cómo se ponen de acuerdo los expertos? ¿Son capaces de formalizar los criterios por los cuales toman su decisión? Si hay desacuerdo entre ellos, ¿cómo se formula tal desacuerdo? ¿Qué metodología usan para evaluar el fenómeno y poner en común una evaluación final? ¿Cómo se matiza tal evaluación? ¿Cuántos expertos es recomendable tener para una evaluación mínimamente fiable? Estas preguntas aparecen en el transcurso de la investigación en música. Por asombroso que parezca, en numerosas ocasiones he visto evaluaciones hechas por un único experto y que el resto de la comunidad ha dado por buena o al menos con muy pocas voces discordantes. De que ese único experto tenía un conocimiento y experiencia formidables no cabía ninguna duda; pero incluso los expertos cometen errores de juicio; pero además no es riguroso aceptar la opinión de un solo experto, por muy prestigioso que este sea. He visto también, por ejemplo, que un experto prestigioso ha basado su evaluación en pequeñísimo número de piezas musicales, a veces tres, pero en otros casos no más de una decena. También aquí parece que falta rigor. Lo observable en un número tan pequeño de piezas puede no ser generalizable al resto y si así lo es habría que justificarlo adecuadamente (normalmente tal justificación está ausente). En el transcurso de mis investigaciones me he encontrado con ejemplos de esta situación, tanto al estudiar artículos como en los proyectos de investigación en que he participado. Por ejemplo, en el caso del flamenco no hay consenso en cuanto a cómo se tiene que transcribir, si bien creando una nueva notación, posiblemente partiendo de la notación occidental, o bien tomando la notación occidental como método único de transcripción. La notación occidental se creó para escribir una música cuyas características no coinciden totalmente con las del flamenco. Además, hay diferencias entre proponer un sistema de transcripción para la guitarra y otro para la voz. La guitarra es un instrumento de afinación fija, pero la voz y menos en el flamenco, no lo es. Donnier para la voz propone un sistema que parte del cante gregoriano [Don11, Don96], pero otros autores como los hermanos Hurtado abogan rotundamente por la notación occidental para todo el flamenco; véase [HH02]. El guitarrista y musicólogo Rafael Hoces, en su tesis doctoral La transcripción para guitarra flamenca [Hoc13], apoya la idea del uso de la notación occidental solo para la transcripción de la guitarra. Entre los flamencólogos, cuando se presenta este debate, algunos llegan a decir es mejor seguir con la notación occidental pues no se alcanzaría acuerdo en diseñar una nueva notación que se adecuase a las peculiaridades del flamenco. De nuevo, aquí estamos en presencia del problema del consenso entre expertos. En los últimos años se está investigando con fuerza los mecanismos que subyacen en la improvisación. Hay dos escuelas de pensamiento al respecto, una que propone que la improvisación se configura a partir de reglas, al estilo de las gramáticas generativas de Chomsky, o trasladado al ámbito músical, al estilo de la teoría generativa de la música de Fred Lerdahl y Ray Jackendoff [LJ03] (véase la serie correspondiente en esta columna [Góm14]). Cada estilo (jazz, flamenco, etc.) tiene sus reglas precisas que hacen que una improvisación se vea dentro del estilo o fuera de él. La otra escuela mantiene que la improvisación se hace a base de patrones, que pueden ser de todo tipo: melódicos, armónicos, rítmicos, formales; y que entonces la calidad de la improvisación está en función de la combinación acertada de esos patrones. Probablemente, la improvisación venga dada por una combinación de ambas. No se sabe, empero, para qué parámetros musicales y en qué grado se produce tal combinación. Investigadores de ambas escuelas de pensamiento han escrito programas que toman, por ejemplo, un corpus de solos de un trompetista de jazz (Parker, Coltrane u otros) y a partir de ese corpus, bien por reglas [GKT10] o por patrones [NSM13], componen solos en su estilo. A la hora de evaluar los resultados del programa, esto es, cuán fielmente se reflejan las características del músico en cuestión, con frecuencia nos encontramos que es la opinión de los autores del artículo el único criterio de evaluación. Los autores afirman que los solos son buenos porque “suenan al trompetista”, o porque “reflejan su pensamiento musical”, pero no aportan razones que sostengan estas afirmaciones. Y no dudo de la honestidad intelectual de estos investigadores, pero desde el punto de vista del rigor metodológico, en ciencia (y la musicología lo es) es difícil aceptar esas afirmaciones. 2. ¿Qué pueden hacer las matemáticas? En otros campos ya ha surgido el problema de alcanzar consenso entre expertos. En medicina, por ejemplo, es un problema que aparece con frecuencia. ¿Cómo lo resuelven en medicina? Hay varios métodos, pero uno de ellos, que goza de cierta popularidad, es el llamado método Delphi. La técnica Delphi es un método para recoger información de expertos y construir consenso a partir de dicha información. Vamos a describir ese método y ver cómo se podría aplicar a la teoría de la música. Jorm [Jor15], en un artículo titulado Using the Delphi expert consensus method in mental health research, investiga la aplicación del método Delphi al acuerdo entre expertos en el campo de la salud mental. El primer paso en la implementación del método es la selección de los expertos. Basándose en el trabajo de Surowiecki [Sur04], el famoso libro The wisdom of crowds: why the many are smarter than the few, propone las siguientes condiciones para elegirlos:
Aunque no en todas las circunstancias el trabajo de un grupo de expertos da buenos resultados, se han estudiado las condiciones bajo las cuales esto ocurre. Hay una gran variedad de contextos en que dicho trabajo es útil y valioso; para más detalles, véanse las referencias del artículo de Jorm [Jor15] (página 888). Hay muchas variantes del método Delphi, sobre todo en función de la aplicación particular, pero se puede describir de forma general como una serie de rondas en que el coordinador del método manda a los expertos unos cuestionarios. Los expertos han de responder a estos cuestionarios y devolverlos al coordinador, quien a su ve estructura la información y los vuelve a mandar a los expertos, quienes, a su vez, han de revisar y criticar sus respuestas anteriores. Este proceso se repite hasta que se alcanza el máximo número de rondas establecido o se alcanza consenso. Asociado al método suele haber tratamiento estadístico de los datos, tanto cuantitativo como cualitativo. Veamos más en concreto cómo se implementa el método Delphi; seguimos aquí el trabajo de Jorm. Los pasos que este establece son los siguientes:
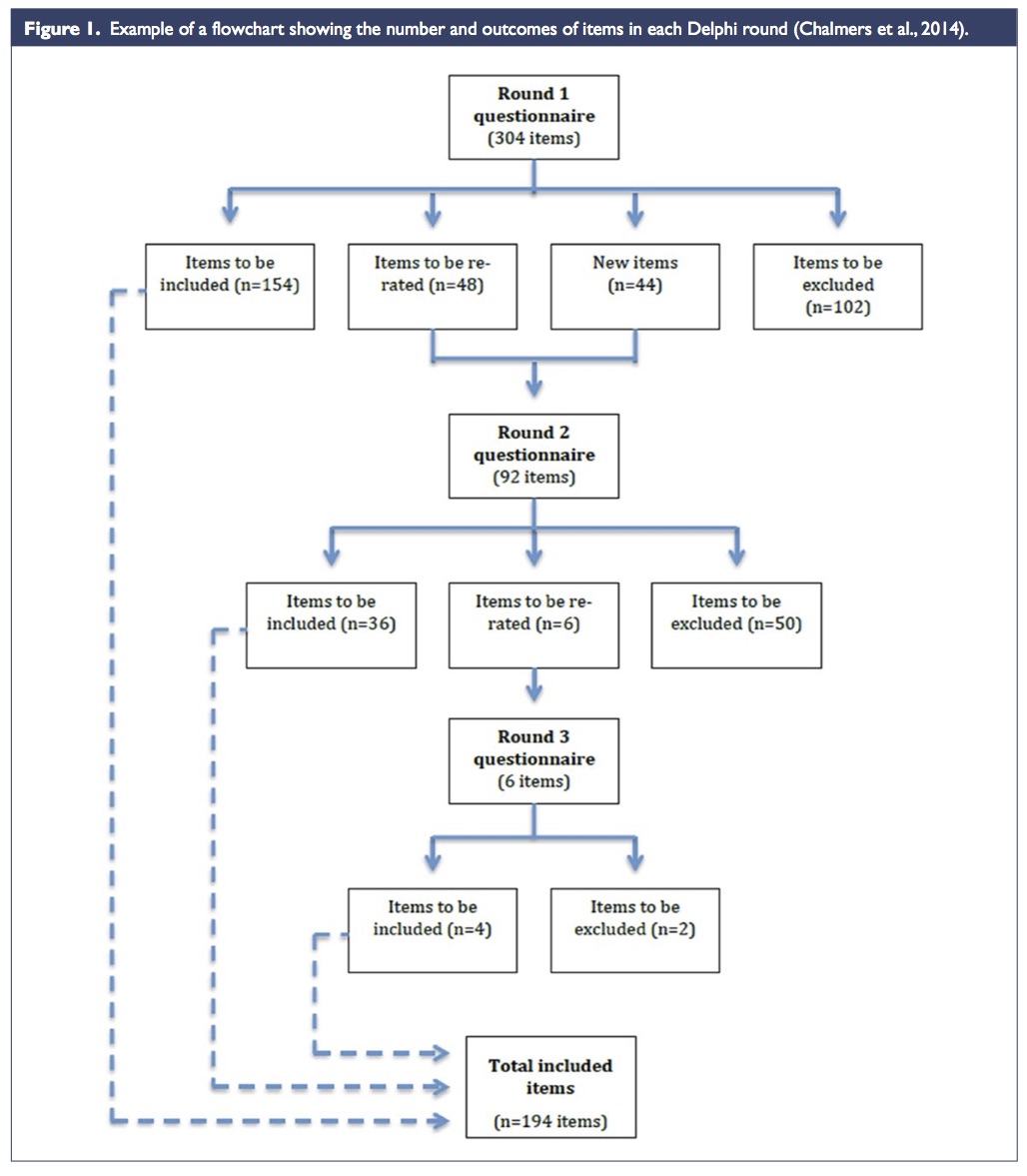
Figura 1: Diagrama de flujo asociado a un proceso Delphi (figura tomada de [Jor15])
En un reciente artículo (junio de 2015), Albert Fornells y sus coautores [FRR+15] aplican la metodología Delphi a problemas de consenso entre expertos en el campo de la hostelería. Los resultados de su método aparecen en forma de mapa conceptual. La formalización matemática de su método es muy alta. Formalizan el razonamiento cualitativo de los expertos usando teoría de conjuntos y tras pasar revista varios índices de consenso, proponen el suyo propio. Los mapas conceptuales los construyen usando técnicas clásicas de agrupamiento tales como los grafos filogenéticos. Este trabajo da una idea del nivel de formalización que se puede introducir en el problema del consenso entre expertos. 3. Conclusiones El método que hemos examinado es totalmente aplicable al problema de alcanzar consenso entre expertos en música. Su uso contribuiría, sin duda, a dar más rigor a las conclusiones en las investigaciones musicales. ¿Cuál es, pues, la contribución de las matemáticas aquí? El rigor; el rigor metodológico. La aplicación de las matemáticas a la música que proponemos en la columna de este mes no está relacionada con la formalización de una propiedad musical en términos matemáticos o en la aplicación de una idea matemática a la composición musical, por poner dos ejemplos clásicos; no, está relacionada con el espíritu de las matemáticas, con la voluntad de rigor que poseen.
Bibliografía [Don96] Ph. Donnier. Flamenco, structures temporelles et processus d’improvisation. PhD thesis, Université Paris X. Nanterre, 1996. [Don11] P. Donnier. Flamenco: elementos para la transcripción. Del cante y de la guitarra. http://divulgamat2.ehu.es/divulgamat15/index.php?option=com_content&view=article&id=12354&directory=67, abril de 2011. [FRR+15] Albert Fornells, Zaida Rodrigo, Xari Rovira, Mónica Sánchez, Ricard Santomà, Francesc Teixidó-Navarro, and Elisabet Golobardes. Promoting consensus in the concept mapping methodology: An application in the hospitality sector. Pattern Recognition Letters, 67:39–48, 2015. [GKT10] J. Gillick, R. M. Keller, and M. Tang, K. Machine learning of jazz grammars. Computer Music Journal, 34:56–66, 2010. [Góm14] P. Gómez. Teoría generativa de la música - I. http://divulgamat2.ehu.es/divulgamat15/index.php?option=com_content&view=article&id=16037&directory=67, junio de 2014. [HH02] A. Hurtado and D. Hurtado. La voz de la tierra: estudio y transcripción de los cantes campesinos en las provincias de Jaén y Córdoba. Junta de Andalucía, Centro Andaluz de Flamenco, Sevilla, 2002. [Hoc13] R. Hoces. La transcripción para guitarra flamenca. PhD thesis, Universidad de Sevilla, 2013. [Jor15] A. F. Jorm. Using the Delphi expert consensus method in mental health research. Australian and New Zealand Journal of Psychiatry, 49(10):887–897, 2015. [LJ03] Fred Lerdahl and Ray Jachendoff. Teoría generativa de la música tonal. Akal, Madrid, 2003. [NSM13] M. Norgaard, J. Spencer, and M. Montiel. Testing cognitive theories by creating a pattern-based probabilistic algorithm for melody and rhythm in jazz improvisation. Psychomusicology, 23:243–254, 2013. [Sur04] J.. Surowiecki. The wisdom of crowds: why the many are smarter than the few. Abacus, Londres, 2004. |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |