 112. SOLUCIÓN CONCURSO DEL VERANO DE 2016
112. SOLUCIÓN CONCURSO DEL VERANO DE 2016 |
 |
 |
 |
| Escrito por Alfonso Jesús Población Sáez |
| Viernes 09 de Septiembre de 2016 |
|
Vuelta a las tareas habituales (algunos antes que otros), aunque el calor se resiste a dejarnos (mirad los remedios de algunas películas para combatirlo en la respuesta C – 7; todavía hay tiempo para ponerlos en práctica). Y cómo no, aquí están las respuestas al cuestionario propuesto. Este año la película propuesta no ha convencido a todos por igual, pero eso sí, es una gran película. Una pequeña aclaración. Repasando las bases del concurso, en ningún sitio se dice que haya que hacer un desarrollo de las soluciones propuestas (al menos alguna indicación de cómo se ha resuelto). Algunos concursantes envían la respuesta final sin explicación alguna. Se ha tomado la decisión, esta vez, de “penalizarlos” muy poquito (un 8 o 9 en lugar del 10), aunque bien podría ser cero esa puntuación. En fin, una nueva aclaración a tener en cuenta para futuras convocatorias. Sin más, vamos a las soluciones. Otros comentarios, en el ejercicio correspondiente. Cuestiones Matemáticas
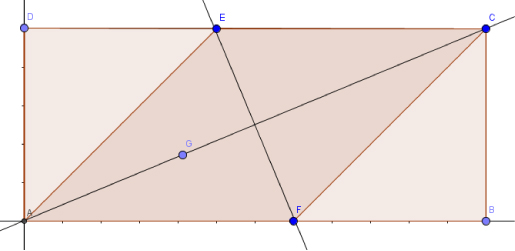
A partir del enunciado, podemos esbozar el dibujo que se muestra a la derecha. Por ser un rombo, los lados AE, AF, EC y FC deben tener la misma longitud, llamémosla m. Sea O la intersección de las diagonales del rombo, que deben ser perpendiculares. Aplicando el teorema de Pitágoras, se tiene que AC2 = AB2 + BC2, de donde AC = Un procedimiento de afrontar la cuestión es mediante coordenadas. Sean A(0, 0), B(a, 0), C(a, b) y D(0, b). La diagonal AC tiene por ecuación y = y – En este apartado nos piden las coordenadas de E, F y G para un rectángulo concreto. Particularicemos entonces. Como AB = 12 y BC = 8, entonces A(0, 0), B(12, 0), C(12, 8), D(0, 8), la diagonal AC tiene por ecuación y = 2x/3, y el punto de corte de las diagonales del rombo O es el centro geométrico del rectángulo inicial, es decir, O(6, 4). Los puntos E y F se encuentran en la perpendicular a AC que pasa por O, que como se ha indicado arriba tiene por ecuación 3x + 2y = 26. Como la única condición adicional es que AFCE sea un rombo, AE = AF = EC = FC = m, existen infinitos valores para E y F, pongamos por ejemplo, m = 8 (no todos los valores de m proporcionan solución ya que la ecuación de segundo grado resultante puede para ciertos valores no tener soluciones reales). En ese caso, sólo hay que resolver el sistema
que nos da los valores E(6 – Finalmente para calcular G debemos previamente hallar la distancia EF, que resulta ser de los puntos anteriores 4√3. Esa distancia sobre la recta AC a partir del origen nos lleva a que G(
Marta, una de las concursantes, ha expresado la solución en forma paramétrica, de un modo muy elegante: E = [6 – 2t, 4+3t], F = [6 + 2t, 4 - 3t], G = [6t, 4t], con 0 < t < 4/3 No todos los participantes han tomado como referencia inicial el mismo punto. En algún caso, el centro geométrico del rectángulo ha sido el punto de partida. M – 2.- Sí, como ya se ha comentado en el apartado anterior, que la solución no es única. Hay infinitos rombos que satisfacen las condiciones del enunciado. M – 3.- La situación ahora es la mostrada en la nueva imagen: los puntos E y F se encuentran sobre los lados AB y CD del rectángulo. En este caso, además de los triángulos rectángulos indicados en el caso anterior, tenemos que FBC también es rectángulo, y por tanto, CF2 – FB2 = CB2
OF2 = AF2– OA2 = ( Por tanto, OF = M – 4.- Como un reloj va tres minutos por delante del otro cada hora, después de veinte horas es cuando irá una hora por delante. M – 5.- Supongamos que la solución es las 23 horas y X minutos (o las 11 horas X minutos, ambas se han dado como correctas). La aguja de los minutos recorre 6º por minuto (360º entre 60 minutos), mientras que la de las horas recorre ½ grado por minuto (360º entre 12 horas = 30º, y 30º entre 60 minutos resulta ½). Si la aguja de las horas está desplazada una distancia x de las once, la aguja de los minutos estará en 35 – x. Aplicando a cada aguja su velocidad de desplazamiento por minuto), se sigue que a 35 – x minutos le corresponden 6(35 – x) grados, mientras que la aguja de las horas se desplaza x/2 grados respecto a las once. Como ambas han de ser iguales, 6(35 – x) = x/2. Resuelta la ecuación nos sale x = 420/13 = 32 + 4/13 minutos, es decir, 32 minutos, 18 y 6/13 segundos. Luego la hora exacta es las 23 horas 32 minutos, 18 y 6/13 segundos. M – 6.- En este caso se trataba de modelizar, a criterio del concursante. Es decir, faltaban datos, sí, pero cada cual podía añadir lo que necesitara para responder a la cuestión. El único dato a respetar era la altura del jarrón. Aclaro esto porque es uno de los ejercicios a mi entender más asequible, pero que menos se ha respondido (sólo dos de seis concursantes). Veamos la solución de Francisco Pi Martínez (un poco resumida):
Dicho esto, el volumen del jarrón se compone de lo siguiente. Definamos, V1 = volumen que engendra el rectángulo al girar sobre su eje. Habitualmente el profesor suele darnos la posibilidad de aplicar el teorema de Pappus-Guldin al cálculo de volúmenes de objetos con simetría de revolución, que es lo que haremos en este caso. El volumen total es V = V1 + V2 – V3 – V4 – V3 + V5 + V6. Calculemos cada volumen. Para ello usaremos la fórmula del teorema, que dice que el volumen engendrado por una superficie al girar alrededor de un eje es igual a la superficie multiplicada por la circunferencia que describe el centro de gravedad de ella al girar, V = S ∙ 2πrg, donde rg es la distancia del centro de gravedad al eje de rotación. Usaremos también la expresión de la coordenada del centro de gravedad de un semicírculo, igual a 4r/3π. V1: Cilindro. r = 5; h = 45; V = π r2 ∙ h = 1125π cm3 V2: Semicírculo de diámetro 3 cm., r2 = 3/2. V3: Dos cuartos de círculo de diámetro 3 cm., r3 = 3/2. V4: Rectángulo. V5: Cuarto de círculo de radio 6 cm., r5 = 6. V6: Triángulo. Sumamos V = V1 + V2 – V3 – V4 – V3 + V5 + V6 = 4095 π /2 + 90 π2 cm3 O lo que es lo mismo, aproximadamente, unos 7.320 cm3, algo más de siete litros. La solución propuesta por Marta Pérez (la que pensé yo), era aproximar (por interpolación, por ejemplo) el perfil mediante una función r(x), y utilizar la expresión V =
Respecto a si es posible hacerlo con menos cuadrados la respuesta es afirmativa. El menor número de cuadrados que se pueden conseguir para hacer un rectángulo perfecto es 9 (más detalles en http://www.squaring.net/sq/sr/spsr/spsr.html). M – 8.- Sea x el número de libros que quedan tras la selección. El proceso de almacenaje en cajas que nos describen queda expresado en términos de congruencias del siguiente modo: x ≡ 3 mod 6 La tercera relación indica que x = 11k. Sustituyendo ese valor en las otras dos relaciones, se tiene que
Como mcd(6, 7) = 1, entonces k = 3 + 42m, de donde x = 11k = 11(3 + 42m) = 33 + 462m Se dice que en la selección se eliminan más de 300 libros, por lo que x < 500. Los únicos valores entonces válidos serán x = 33 para m = 0, y x = 495 para m = 1. Como se dice que los dígitos son todos distintos, entonces la única solución será 495 libros. M – 9.- Sea V(t) el volumen de agua de la bañera en el instante t. Como la variación del volumen es proporcional a la cantidad de agua existente en cada momento, V’(t) = λ V(t), y V(0) = 350, V(4) = 315. Se trata de una sencilla ecuación diferencial de primer orden en variables separadas, así que dejando en un miembro las V y en el otro la constante λ, e integrando, se llega a que V(t) = α eλt
Para t = 0, 350 = α. Despejando λ, se tiene que V(t) = 350 (10/9)-t/4 . Después nos preguntan por el momento en que el volumen de agua es la mitad del inicial, esto es, 175 litros. Despejando t, se obtiene que eso sucede cuando t = Por tanto, el bañista no se percató de que el tapón estaba quitado ya que pidió a su interlocutor la toalla mucho antes (por lo que vemos en la película). M – 10.- Un sencillo ejercicio de probabilidades. Lo más sencillo es elaborar un diagrama con todas las posibilidades de elección, y de ahí calculas las probabilidades. Éstas finalmente son: a) p(tres hombres) = Son, respectivamente, las probabilidades de elegir Hombre – Hombre – Mujer, Hombre – Mujer – Hombre y Mujer – Hombre – Hombre. Nótese que las tres son idénticas. Esto podría deducirse a priori. Dos hombres y una mujer pueden distribuirse de tres formas diferentes, por lo que bastaría con haber hecho 3 ( c) p(al menos un hombre) = 1 – d) Podemos resolver este apartado al menos de dos modos distintos. Por un lado, si las dos primeras elecciones fueron dos hombres, entonces para la tercera persona se selecciona entre 12 mujeres y 14 hombres. En ese caso la probabilidad de que la siguiente sea mujer será p = 12/26 = 6/13 ≈ 0.4615.... Si echamos mano de la probabilidad condicionada, utilizando la notación Mi ≡ Mujer en el lugar i-ésimo entonces, p(M3 / H1 H2) = Si nos fijamos un poco en la simplificación final, podemos observar que en realidad hacerlo mediante este segundo método no es apenas significativo en este caso (los dos primeros factores desaparecen, quedando únicamente el tercero, lo que sugiere que el procedimiento no aporta nada y que lo que hay que hacer es razonarlo de la primera manera).
Un recorrido por el apartamento pasando una vez por cada puerta y volviendo al punto de partida es un camino euleriano cerrado en el grafo. Pero éste tiene dos vértices de grado impar, por lo que tal recorrido no es posible. Si se duplica la arista B-Pasillo (son los dos vértices de grado impar), se obtiene un nuevo grafo G* que sí es euleriano. Un camino euleriano cerrado en este grafo, que empiece y termine en el exterior podría ser entonces así: Ext. – A – Pas. – A – B – Pas. – B – C – D – E – Pas. – E – Ext. y este recorrido es el que nos piden en la segunda parte, pues sólo se repite el paso por la puerta que comunica la sala B con el pasillo. M – 12.- El grafo que se debe considerar ahora es el que resulta de suprimir el vértice exterior en el grafo G.
Una 3-coloración del grafo simple asociado se muestra en la imagen. Una explicación menos “técnica” (y seguramente más entendible por un mayor número de lectores), nos la proporciona uno de los concursantes, Francisco Pi: “Fijémonos en el punto en que coinciden los límites de las habitaciones A, B y el pasillo. M – 13.- El resultado de la operación es 1944, año de estreno de la película buscada. La razón por la que da ese resultado sin realizar “demasiadas operaciones”, es la siguiente: si hacemos que 2016 = x, entonces la fracción queda de este modo
que factorizada y simplificada resulta sencillamente x. O sea que queda 2016 (1 – (1/28)) = 1944. Cuestiones sobre cine C – 1.- Películas en las que no se sabe al final que ha sucedido: dos clásicos son El sueño eterno (The big sleep, Howard Hawks, EE. UU., 1946) y Rashomon (Akira Kurosawa, Japón, 1950). culas en las que el crimen quede impune: ha sucedido:
Los concursantes han aportado además los siguientes títulos: Los invitados (Víctor Alcázar, España, 1987), Sospechosos Habituales (The Usual Suspects, Bryan Singer, EE. UU., 1995), Minority Report (Steven Spielberg, EE. UU., 2002), Última llamada (Phone Booth, Joel Schumacher, EE. UU., 2002), Zodiac (Zodiac, David Fincher, EE. UU., 2007), La cinta blanca (Das weiße Band - Eine deutsche Kindergeschichte, Michael Haneke, Austria/Alemania/Francia/Italia, 2009), La Granja (Tannöd, Bettina Oberli, Suiza, 2009), El profesor Layton y la Diva Eterna (Masakazu Hashimoto, Japón, 2009). Novelas en las que no se sabe al final que ha sucedido: En este caso sirven muchas de las películas anteriormente citadas, ya que éstas suelen basarse en sus homólogos relatos, novelas, ensayos, etc. Así los concursantes han venido refiriéndose en este apartado también a El sueño eterno, de Raymond Chandler (publicado en 1939), Minority Report, relato de Philip K. Dick (publicado en 1956), Los invitados, novela homónima de Alfonso Grosso publicada en 1975, Zodiac: El asesino del zodiaco, de Robert Graysmith (publicado en versión original en 1986), Tannöd, el lugar del crimen, novela de Andrea Maria Schenkel (2008). Entre aquellos que no se han llevado al cine (que yo sepa) se han citado El barril de amontillado, cuento de Edgar Allan Poe publicado en 1846. Películas en las que el crimen quede impune: Hay bastantes, sobre todo me viene a la cabeza las que tienen que ver con juicios. Por ejemplo, Testigo de Cargo (Witness for the Prosecution, Billy Wilder, EE. UU., 1957), y muchas de las dirigidas por Sidney Lumet, como 12 hombres sin piedad (Twelve Angry Men, EE. UU., 1957) o Veredicto Final (The Verdict, EE. UU., 1982), entre otras. Los concursantes añaden El secreto de la pirámide (Young Sherlock Holmes, Barry Levinson, EE. UU., 1985), El silencio de los corderos (The Silence of the Lambs, Jonathan Demme, EE. UU., 1991), Sommersby (Jon Amiel, EE. UU., 1993), Ocean's Eleven: Hagan juego (Ocean’s Eleven, Steven Soderbergh, EE. UU., 2001), Saw (James Wan, EE. UU., 2004), Fast & Furious 5 (Justin Lin, EE. UU., 2011).
Los concursantes por su parte han señalado la presencia del cubo de Rubik en En busca de la felicidad (The Pursuit of Happyness, Gabriele Muccino, EE. UU., 2006), Perdita Durango (Álex de la Iglesia, España, 1997), Drive (Nicolas Winding Refn, EE. UU., 2011), Gravity (Alfonso Cuarón, EE. UU., 2013), Plan de escape (Escape plan, Mikael Håfström, EE. UU., 2013) (en esta aparecen también otros rompecabezas de madera), o Hal (Haru, Ryoutarou Makihara, Japón, 2013). En la imagen, otra conocida película en la que aparece.
Se ha citado El motín del Caine, recordando cómo Humphrey Bogart movía compulsivamente unas bolas metálicas (la expresión “bolas chinas” se refiere a otra cosa, por cierto). Esta no la podemos dar por válida ya que en realidad no es un juego ni rompecabezas concreto. El protagonista mueve esas bolas como podía morderse las uñas, o arañarse, como tic de su desquiciada mente.
C – 3.- El reloj es regalo de Waldo a la protagonista. Él tiene otro exactamente igual en su casa. Y es fundamental en el desarrollo de la trama porque es en ese reloj donde guarda algo importante.
C – 4.- En Sólo ante el peligro (High Noon, Fred Zinnemann, EE. UU., 1952) la película transcurre a la vez que la acción. El paso del tiempo, marcado por diversos relojes, se convierte en uno de los protagonistas, marcando la implacable e inevitable cuenta atrás. También el reloj es protagonista en El extraño (The Stranger, Orson Welles, EE. UU., 1946), El reloj asesino (The Big Clock, John Farrow, EE. UU., 1948), en todas aquellas películas en las que hay viajes en el tiempo (El tiempo en sus manos, la saga Regreso al Futuro, Atrapado en el tiempo, etc.), el reloj carillón de La muerte tenía un precio (Per qualche dollaro in più, Sergio Leone, Italia, 1965). Los concursantes han propuesto, entre otras además de alguna de las mencionadas, las siguientes: Tiempos modernos (Modern Times, Charles Chaplin, EE. UU., 1936), Sed de mal (Touch of Evil, Orson Welles, EE. UU., 1958) (reloj bomba al inicio de la película), Atraco a las 3 (José María Forqué, España, 1962), El tren de las 3:10 (3:10 to Yuma, Delmer Daves, EE. UU., 1957), El hombre mosca (Safety Last!, Fred C. Newmeyer, Sam Taylor, EE. UU., 1923), Matar un ruiseñor (To Kill a Mockingbird, Robert Mulligan, EE. UU., 1962), El gran salto (The Hudsucker Proxy, Joel y Ethan Coen, EE. UU., 1994), las diferentes versiones de Alicia en el país de las maravillas, etc. C – 5.- Se trata de un cuadro. Cuadros como en El retrato de Dorian Gray (The Picture of Dorian Gray, Albert Lewin, EE. UU., 1945), La mujer del cuadro (The Woman in the Window, Fritz Lang EE. UU., 1944), Las dos señoras Carroll (The two Mrs. Carroll, Peter Godfrey, EE. UU., 1947), Jennie (Portrait of Jennie, William Dieterle, EE. UU., 1948), Pasos en la niebla (Footsteps in the Fog, Arthur Lubin, Reino Unido, 1955), Vértigo (De entre los muertos) (Vertigo, Alfred Hitchcock, EE. UU., 1958). Recientemente, La dama de oro (Woman in Gold, Simon Curtis, Reino Unido, 2015) también gira en torno a un famoso cuadro, en este caso la lucha por su recuperación tras el expolio nazi durante la II Guerra Mundial. C – 6.- El retrato de Laura, que además de la película que nos ocupa, aparece en las películas En la Costa Azul (On the Riviera, Walter Lang, EE. UU., 1951) y El mundo es de las mujeres (Woman’s World, Jean Negulesco, EE. UU., 1954). La primera también la protagoniza Gene Tierney, y la segunda Clifton Webb. Como curiosidad decir que en realidad no es un retrato sino una fotografía ampliada que posteriormente se repasó cuidadosamente al óleo tratando de lograr un aire de etereidad. Clifton Webb, no era demasiado apreciado en Hollywood al que consideraban un exigente y decadente snob. Además era homosexual y tenía un estilo afectado que podría transmitir a la pantalla y quitar credibilidad a sus personajes. No trabajaba en el cine desde 1925 (la mayor parte de su carrera fue en el teatro), y fue una apuesta personal del director Otto Preminger. A partir de este papel, logró hacerse un sitio en la gran pantalla con papeles muy similares (por curiosidad, echen un vistazo a su siguiente película, Envuelto en la sombra (The dark corner, Henry Hathaway, EE. UU., 1946)), entre los que destaca El filo de la navaja o su caracterización de Mr. Belvedere en Niñera moderna, Mr. Belvedere estudiante y El genio se divierte. Y una curiosidad final: Gene Tierney y Clifton Webb nacieron el mismo día (de distintos años, obviamente).
C – 7.- Casi todos los concursantes dan los mismos ejemplos. (¡¡Ay, Marilyn, cómo te recuerdan!!). En La tentación vive arriba (The Seven Year Itch, Billy Wilder, EE. UU., 1955), Marilyn Monroe se pone sobre una rejilla de ventilación del metro de Nueva York para refrescarse. También metía las bragas (con perdón) en el frigorífico antes de ponérselas. Por otro lado, en las tórridas noches madrileñas, Carmen Maura pide que la rieguen en plena calle (La ley del deseo, Pedro Almodóvar, España, 1987). En La ventana indiscreta (Rear Window, Alfred Hitchcock, EE. UU., 1954), los protagonistas abren las ventanas de par en par para intentar refrescarse. También hace bastante calor en La gata sobre el tejado de zinc (Cat on a Hot Tin Roof, Richard Brooks, EE. UU., 1958), y se combate el calor a base de ropa ligera (aunque bebiendo whisky a la vez no sé si el efecto servirá). Temperaturas altas (por diferentes razones) las padecen también los protagonistas de Fuego en el Cuerpo (Body Heat, Lawrence Kasdan, EE. UU., 1981) que tratan de paliar (no parece que lo logren) a base de añadir cubitos de hielo a la bañera en la que descansan,...., cuando pueden.
C – 8.- Son muchos. Entre los más llamativos están la pitillera que Laura regala a Shelby y que luego éste vende, las llaves de la casa de campo, la botella de whisky barato, los objetos personales de Laura (perfume, cartas, diario...) C – 9.- La novela original fue escrita por Vera Caspary (1899 – 1987), autora de dieciocho novelas, cuatro obras de teatro y diez guiones de películas. Era especialista en relatos de asesinatos. En la actualidad, el escritor James Ellroy (autor, entre otras obras de L. A. Confidential) pretende rescribir la obra, manteniendo la trama principal aunque trasladándola a Londres y con la presencia de Scotland Yard. Al parecer el asesinato de Laura Hunt le recuerda al de su propia madre, Geneva, y por extensión al de La dalia Negra (otra de sus obras). Respecto a los actores actuales a los que los concursantes han elegido como posibles para la nueva versión del proyecto del remake de la película, éstos han sido: Para Laura, Scarlett Johansson y Nicole Kidman, como detective a Gary Oldman y George Clooney, como Waldo a William H. Macy y Jim Carrey, finalmente como Shelby Carpenter a John Leguizamo y Christian Bale. Propuestas muy diferentes. Ya comprobaremos si los productores tendrán la misma idea.... C – 10.- Evidentemente la película es Laura (Otto Preminger, EE. UU., 1944), y haya gustado o no, es una gran película. Según uno de esos rankings a los que tan aficionados son los anglosajones, es la película nº 288 entre las 1001 que hay que ver antes de morir. La crítica la da en general del 8 en adelante en un baremo hasta 10 (suelen tener más razones objetivas que los espectadores para otorgar una calificación, pero también es un parámetro relativo). Lo que queda fuera de toda duda es que es una de esas películas de la época dorada del cine norteamericano, con un buen guión, una buena interpretación y una excelente dirección.
Puntuaciones de los Concursantes Como cada año, las distancias son mínimas (lo cual dice mucho a favor de los participantes; enhorabuena a todos, y también a quienes lo hayan intentado y finalmente no se hayan atrevido a mandar sus respuestas), las puntuaciones altas, y la fidelidad encomiable (en esta ocasión han habido nuevos participantes, incluyendo la ganadora; bienvenidos): Marta Pérez ...................... 198 En unos días recibiréis un correo electrónico (no sé si todos o sólo los primeros, depende de las existencias de regalos), para que nos facilitéis una dirección postal a la que enviaros el obsequio. Muchas Gracias por vuestra participación. |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |






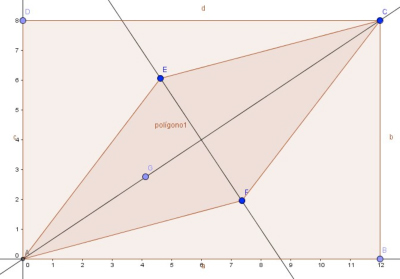 M – 1.-
M – 1.-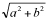 , y OA = (½)AC. De nuevo por Pitágoras, OF2 = AF2 – OA2.
, y OA = (½)AC. De nuevo por Pitágoras, OF2 = AF2 – OA2.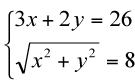
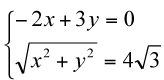
 Siendo como antes m el lado del rombo, m2 – (x – m)2 = y2, de donde se obtiene que m =
Siendo como antes m el lado del rombo, m2 – (x – m)2 = y2, de donde se obtiene que m = 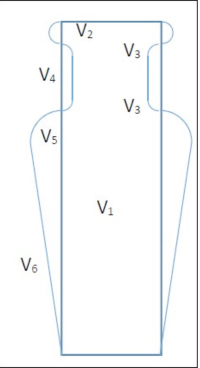 Si la altura es 45 cm. de alto, supongamos que la anchura de la boca son 10 cm. por el interior (obsérvese la figura). Según esto, el rectángulo representado es de 10 cm. por 45 cm. Las semicircunferencias superiores tienen un diámetro de 3 cm. al igual que los arcos pequeñitos que continúan hacia abajo. Hay un tramo recto de 6 cm. El arco que sigue (después del pequeño ya comentado) tiene un radio de 6 cm. La recta (que junto con el lado del rectángulo y algo de imaginación determina un triángulo) abarca los 27 cm. restantes.
Si la altura es 45 cm. de alto, supongamos que la anchura de la boca son 10 cm. por el interior (obsérvese la figura). Según esto, el rectángulo representado es de 10 cm. por 45 cm. Las semicircunferencias superiores tienen un diámetro de 3 cm. al igual que los arcos pequeñitos que continúan hacia abajo. Hay un tramo recto de 6 cm. El arco que sigue (después del pequeño ya comentado) tiene un radio de 6 cm. La recta (que junto con el lado del rectángulo y algo de imaginación determina un triángulo) abarca los 27 cm. restantes.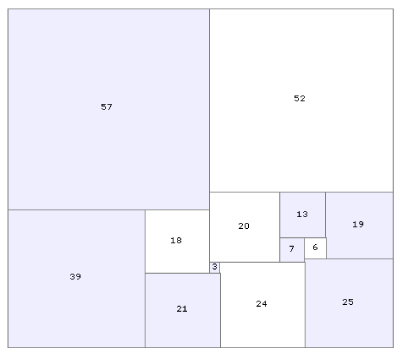 M – 7.-
M – 7.- Dando valores a t a partir de las condiciones iniciales, obtenemos las constantes α y λ:
Dando valores a t a partir de las condiciones iniciales, obtenemos las constantes α y λ: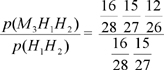 = 6/13
= 6/13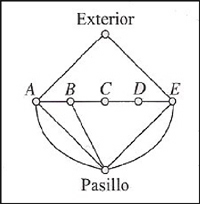 M – 11.-
M – 11.-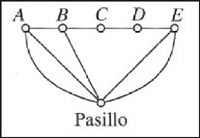
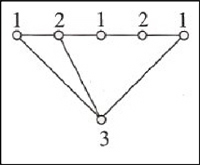 El mínimo número de colores necesarios para pintar las salas y el pasillo es el número cromático de este nuevo grafo. Este grafo contiene triángulos y admite una 3-coloración, luego dicho número cromático es 3.
El mínimo número de colores necesarios para pintar las salas y el pasillo es el número cromático de este nuevo grafo. Este grafo contiene triángulos y admite una 3-coloración, luego dicho número cromático es 3.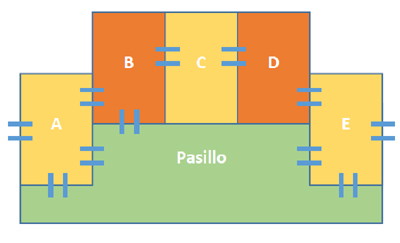 Los tres pares que se pueden formar entre estos tres recintos están comunicados por puertas. Si utilizo solo dos colores, es obvio (principio del palomar) que habrá dos recintos pintados del mismo color. Y como todos los pares están comunicados por puertas, ya no cumpliría el enunciado. No es posible con solo dos colores”. Para tres, adjunta una posible coloración (la misma puesta arriba).
Los tres pares que se pueden formar entre estos tres recintos están comunicados por puertas. Si utilizo solo dos colores, es obvio (principio del palomar) que habrá dos recintos pintados del mismo color. Y como todos los pares están comunicados por puertas, ya no cumpliría el enunciado. No es posible con solo dos colores”. Para tres, adjunta una posible coloración (la misma puesta arriba). C – 2.-
C – 2.- También se ha mencionado las torres de Hanoi en El origen del planeta de los simios (Rise of the Planet of the Apes, Rupert Wyatt, EE. UU., 2011).
También se ha mencionado las torres de Hanoi en El origen del planeta de los simios (Rise of the Planet of the Apes, Rupert Wyatt, EE. UU., 2011).