 116. Año nuevo, libro nuevo
116. Año nuevo, libro nuevo |
 |
 |
 |
| Escrito por Alfonso Jesús Población Sáez |
| Miércoles 04 de Enero de 2017 |
|
Continúa creciendo la bibliografía que difunde las matemáticas a partir de un marco cinematográfico. Nos damos un paseo por sus contenidos indicando lo que más nos ha gustado y algunas cosillas (pocas) matizables.
Debemos advertir al lector de estas líneas que esta reseña no es todo lo objetiva que debería ser. La razón no es otra que la dedicación del que esto escribe a este mismo tema, lo que conlleva la lectura y el análisis de todas las publicaciones y reseñas en páginas web que caen por sus manos (podéis constatarlo en artículos previos de esta misma sección), que son muchas, que van apareciendo. Esto hace que estemos al tanto de cada nueva película, cada nuevo comentario que suscitan, y a su vez que muchas cosas nos resulten ya tratadas anteriormente. Esa sensación no la van a tener los que se acerquen al libro sin todo ese bagaje, encontrando por ello quizá desmesurado algún comentario que pueda hacerse en lo que sigue, aunque conscientes de ello, hemos tratado de mitigarlo lo más posible. En todo caso, todo lo que se expone, siendo subjetivo, trata de ser razonado, y siempre con ánimo constructivo y desde un profundo cariño y camaradería que creemos que existe entre los cuatro o cinco compañeros que nos hemos “especializado” de algún modo en utilizar esta relación entre el cine y las matemáticas para un objetivo común y compartido: mostrar las matemáticas desde otras ópticas diferentes a las tradicionales, e intentar que los lectores las aprecien como merecen. En cualquier caso, el libro nos presenta las suficientes referencias no consignadas en ningún otro lugar como para que resulte de interés para todos. No detallaremos cuáles son unas y otras a fin de que el lector se sienta “con ganas de más” al finalizar la lectura y se acerque al resto de referencias, muchas de ellas consignadas con detalle en la bibliografía del libro. Una característica que el autor ha tratado de mantener a lo largo de sus páginas es su sencillez: que nadie tema el tratamiento matemático, de un nivel asequible para todo el mundo (por supuesto que este calificativo es asimismo subjetivo, pero lo cierto es que nadie que haya superado la ESO debería tener dificultad alguna para seguir las explicaciones del texto, por muy olvidadas que crea tener las matemáticas). No en vano, su autor conoce de primera mano, dada su experiencia docente, cómo introducir y describir los conceptos y en qué lugares pueden “cojear” los potenciales lectores, poniendo ahí el énfasis preciso. Se puede decir que se trata de un libro con más matemáticas sugeridas que explícitas. Pero un libro de divulgación se nutre inevitablemente de algo más para que su lectura atraiga. Ese plus nos lo aportan las referencias culturales que rodean a las películas tratadas: curiosidades; relación con el arte, la pintura, la literatura, etc., con otras producciones cinematográficas; apuntes de tipo histórico y detalles biográficos de cineastas, matemáticos, científicos, etc. Por ponerle, muy forzadamente, algún pero, quizá éste se encuentre en la parte cinematográfica en la que en algunos momentos uno recuerda títulos o datos que pueden completar la información, pero nadie dijo que el objetivo fuera hacer un repaso exhaustivo de éste o aquél tema, además de que son las matemáticas, no el cine, el vehículo que marca el recorrido, por no mencionar el incremento del número de páginas que, sin duda, conllevaría lo que pudiera provocar disminuir el atractivo del libro. Así pues, se opta por una selección personal de las referencias de tipo cinematográfico, bien justificada, por cierto. La bibliografía por capítulos resulta, como ya se ha dicho, adecuada y bien detallada, tanto en las referencias matemáticas como en las de las películas, indicando en aquellas que lo permiten, las direcciones electrónicas de los artículos y/o trabajos que han servido como documentación, lo que es muy de agradecer para que el lector que desee ampliar algún aspecto pueda recurrir a esas fuentes. Es de justicia también, como hace el autor en éste y el anterior volumen, reconocer el trabajo de nuestro compañero Ángel Requena (responsable de la sugerente sección Instantáneas Matemáticas en este mismo portal, DivulgaMAT) por su labor de revisión y aporte de sugerencias, tan laboriosa como perspicaz. En este enlace puede consultarse la ficha del libro y una breve introducción del autor; en este otro, el índice detallado. Vayamos a continuación capítulo a capítulo describiendo brevemente los tópicos contemplados de un modo sintético. Cuestión de tamaños.- Dos son los grandes protagonistas de este capítulo: King Kong y Gulliver. Se aborda y deja clara la imposibilidad de la existencia de seres de estas características y otros primos-hermanos (Godzilla y otros monstruos, hombres menguantes y mujeres de 50 pies) del cine. La herramienta fundamental será la ley cuadrado-cúbica de Galileo con la que se aplican resultados de semejanza y proporciones. No es un tema novedoso, de hecho, se ha tratado en diferentes artículos (que se citan y comentan en la bibliografía, insistimos), pero como ya se indicó anteriormente, nunca está de más recopilarlos y comentarlos desde una perspectiva más personal, ya que para muchos seguramente sean novedosos. Vampiros y estafas exponenciales.- Se aborda el tema de si es posible la desaparición de la humanidad, ya sea mediante una amenaza vampírica, o de zombies, dos de las que el cine ha venido proponiendo prácticamente desde sus inicios. Empezando por este último caso, a raíz del comentario de Soy Leyenda, echamos en falta las dos referencias previas (bastante mejores desde un punto de vista cinematográfico, para mi gusto: El último hombre sobre la Tierra (1964) y El último hombre vivo (1971), si bien en efecto es la consignada la que suministra más datos numéricos para poder comentar). En cuanto a los vampiros, se recuerdan los razonamientos que hacen imposible su existencia tal y como se han descrito tradicionalmente en literatura y cine (célebre artículo de Efthimiou y Gandhi) en base al inevitable crecimiento exponencial. Pero los explotadores de mitos no se rinden a seguir haciendo caja, así que han venido transformando las costumbres y evoluciones de estos seres para que haya que idear a su vez otros argumentos de su inverosimilitud. Algunos de ellos también se comentan. A pesar de ser la función exponencial una de las funciones elementales que más atención se presta en los estudios básicos, tampoco dejan de aparecer periódicamente estafas de tipo piramidal. Con ellas finaliza con gran acierto, y yo creo que interés, este capítulo (la analogía vampírico-piramidal es de lo más adecuada). La única matización que haría volvería a ser respecto a un comentario de cine. Se dice que “en las películas de Hollywood, aunque se recree el encanto de los canallas, existe la norma no escrita de que al final debe hacerse justicia”. Esa conclusión, siendo cierta en un alto porcentaje de casos (épocas de caza de brujas, cine comercial actual políticamente correcto), no siempre ha sido (años setenta, por ejemplo) ni es así (cine actual de autor y/o cine independiente). Páginas atrás se dice que las matemáticas nos muestran que hay problemas sin solución, o con infinitas. Yo añadiría además que cuando se trata de situaciones reales, como esto de la norma no escrita, hay tantas variables a considerar que podemos caer en la extrapolación, por lo que la generalización no suele ser buena consejera (en las declaraciones de personajes públicos lo vemos diariamente). Afortunadamente otras filmografías muestran argumentos más realistas (incluyendo la española, que a mucha gente no gusta, quizá entre otras cosas por no predominar esos finales felices, salvo en comedias, y por concebirse el cine por parte de muchos espectadores únicamente como evasión). En cuanto a las matemáticas, además de lo ya comentado se alude a la interpolación polinómica, los logaritmos y los números vampiros. Atrapa el gazapo.- El capítulo más extenso, que recopila muchas de las erratas (desde perdonables equivocaciones a auténticos disparates) que el autor ha ido publicando en sus reseñas en la revista SUMA, junto a otras de diferente procedencia y algunas nuevas. Particularmente me parece muy acertada la digresión acerca de que no se deben identificar matemáticas con aritmética (es confundir una parte, la herramienta, el cálculo aritmético, con el todo), y que el verdadero alma de las matemáticas está en la resolución de problemas. No me resisto a reproducir la frase de Conrad Wolfram que se incluye: Paremos de enseñar a calcular, y empecemos a enseñar matemáticas). El cálculo es necesario, pero no lo único, ni el fin. Es como si estuviéramos todo el curso aprendiendo las reglas del parchís, y al final no jugáramos nunca. Pues eso es lo que hacemos habitualmente con las matemáticas. Sorando expresa su deseo en uno de los párrafos del capítulo en no ser un cazador cazado, es decir, que ninguno de los gazapos expuestos pueda volverse en su contra. Es un deseo loable, pero no sé sabe cómo ni porqué (y yo mismo he sido víctima de tales circunstancias; por más que se lea, se relea y se repase algo mil veces), siempre se escapa alguna errata, parece algo incontrolable. Unas páginas atrás, el autor dedica comentarios algo duros a propósito de El Mejor (The Greatest, 2009): “Esta ocurrencia es realmente patética y tiene un sitio destacado en una antología de disparates matemáticos del cine. ¿Será posible que nadie del equipo de rodaje supiese qué es una integral, qué es un logaritmo y cómo su cálculo hoy con la calculadora no dure tres años sino lo que se tarde en teclear las instrucciones?” La ocurrencia es decir (Pierce Brosnan): “Es una de las integrales más difíciles que he solucionado en mi vida; tardé tres años en hacerlo…”, y lo que vemos escrito en el vientre de la embarazada protagonista es 4 log(2+√3) − (2π/3)
Reto: ¿se atreve alguien a indicar un problema o situación donde el resultado sea el valor anterior? Matemáticas en el lado oscuro.- Recopilación de escenas matemático-diabólicas desde tres puntos de vista diferentes, descendiendo de lo general a lo particular: la maldad demoniaca (caso de que exista tal ente), la de los regímenes totalitarios (esa sí, desgraciadamente, existe y no parece estar en peligro de extinción; magnífica reflexión en el libro), y la que han llevado a cabo ciertos individuos (tanto reales como en la ficción cinematográfica; mención de algunos psicópatas matemáticos). Se comenta también una cierta tendencia a demonizar la ciencia por parte de algunos interesados en que siga vigente el oscurantismo y/o la superstición. Aritmética binaria, combinatoria (combinaciones y permutaciones), proposiciones lógicas, método de inducción completa con ejemplo de aplicación (suma de los primeros números naturales), axiomas de Peano, proporción áurea y número phi, son algunos de los tópicos matemáticos que se repasan en este capítulo. Matemáticas contra el crimen.- Las matemáticas también han permitido desarrollar algunas técnicas de investigación policial. Todo ello constituye una magnífica ocasión para recordar desde la más simple aritmética (pero bien aplicada) o el comportamiento de la función exponencial negativa (desintegración radiactiva), a resultados más elaborados como la ley de Bendford, los fractales y el movimiento browniano o el RSA. Ecuaciones Decisivas.- Volviendo a la subjetividad de estas líneas, puedo declarar que este es el capítulo que más me ha gustado. En él se analizan las diferentes intenciones que los cineastas han venido marcando con la inclusión de fórmulas en sus películas, para la mayor parte de los espectadores uno de los símbolos más claros, sino el que más, por el que perciben que hay matemáticas en una escena. Las situaciones elegidas lo son en ámbitos muy diferentes (lo que vuelve a poner de manifiesto aquello de que las matemáticas están en todas partes). Así, la subsistencia de la humanidad puede depender de que los cálculos sean correctos (aunque pueda parecer ciencia ficción, se explica brevemente cómo en la actualidad se han desarrollado modelos matemáticos para casi cualquier cosa, y algunos son realmente útiles), el éxito o fracaso de una película de que se hayan medido bien ciertos parámetros ajenos al marketing publicitario, estimaciones de cómo se van a comportar los mercados financieros o la intención de voto de los ciudadanos, etc. Por supuesto, las pizarras llenas de fórmulas a veces también son de lo más absurdo y surrealista (como lo de intentar dormir a los ciudadanos de una población gracias a la ecuación de segundo grado (no por explicarla, ojo, sino aplicándola en una máquina por la que suspirarían cientos de insomnes), medir la belleza y grandeza de una poesía o describir la fórmula de la felicidad). ¡Houston, tenemos un problema!.- Como sugiere el título, se da un repaso a algunos de los más recientes estrenos relacionados con diferentes peripecias espaciales. En ellas se intuyen mucha ciencia y muchas matemáticas pero a nivel teórico, con pocos detalles concretados (el público desea entretenerse, no ver un documental). Pero ahí es donde este tipo de lecturas son de interés, para señalar que hay matemáticas, aunque no se expliciten. Y por eso son tan importantes (imprescindibles, yo diría, pero no quiero que nadie se moleste o vea en ello una exagerada manifestación de prepotencia de los matemáticos, pero la realidad es la que es; traten de vivir sin nada en las que intervengan las matemáticas a ver que pasa). Se describen con detalle las circunstancias en las que las matemáticas están en Marte, comprobando si las cuentas reales corroboran lo indicado en la película; la única pega es que se debería advertir que se lea después de haber visto la película porque en este caso (único en todo el libro), se cuenta todo lo que va a pasar en ella y eso podría echar atrás a los que no la hayan visto más que animarlos a hacerlo. Se vuelve a destacar la importancia de saber aplicar las herramientas matemáticas para resolver problemas, enunciándose algunos de los diferentes procedimientos más habituales para hacerlo. Para vivir.- Y las matemáticas nos hacen la vida más cómoda y fácil. En lo más primario, para contar. Además superan el estereotipo de frías y calculadoras (puro materialismo, en suma) con que las califican los que no han llegado ni han querido hacer el esfuerzo de profundizar un poco en ellas, mostrándonos algunas situaciones en las que permiten fomentar valores como la libertad (ligada a la abstracción con que el investigador o estudioso se entrega por difíciles que sean las situaciones en las que están inmersos), la igualdad entre personas (amplio apartado sobre la histórica injusticia a la que se ha sometido a las mujeres matemáticas tomando como ejemplo la vida personal y profesional de Sofía Kovalevskaya y Sophie Germain), y la fraternidad (enmarcada en este caso en la historia de Ramanujan y G. H. Hardy y sus trabajos a pesar de las dificultades marcadas por su diferente filosofía, cultura, personalidad, ideales, etc.). En la conclusión final, José María Sorando sintetiza su sentir a lo largo de sus años de docencia respecto a lo que a su juicio debería primar en las aulas por parte del profesorado: la emoción del descubrimiento tratando de apartar un poco la mecanización, la memorización vacía (permítaseme el símil navideño de engordar el pavo hasta cargárnoslo o que lo mande todo a paseo) y potenciar unas matemáticas prácticas que permitan al futuro ciudadano primero no dejarse engañar y ser crítico, y llegando al óptimo, que fuera capaz de apreciar en su justa medida la belleza que esta disciplina encierra más allá de un temario que hay que acabar a toda costa. Ojalá más docentes se subieran a este carro, y ojalá se consiguiera algún avance en este sentido. Un primer paso: leer y disfrutar de lecturas que complementen las “formales” como la de este libro. Esta dirección electrónica esta protegida contra spambots. Es necesario activar Javascript para visualizarla |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |






 Apenas transcurrido un año de la publicación de Aventuras Matemáticas en el Cine (Editorial Guadalmazán, octubre 2015), José María Sorando nos propone una nueva entrega enmarcada en esos dos campos tan apreciados por los lectores de esta sección, el cine y las matemáticas. En esta ocasión, se nos indica en el prólogo que el leitmotiv son algunos Desastres Matemáticos en el Cine, entendidos en un amplio sentido, tanto que el título final es Resolviendo Problemas, que a la postre constituirá el deseo del autor sobre lo que debería ser el objetivo del estudio de esta disciplina. Hasta llegar ahí, recorremos un camino jalonado por diferentes etapas, entre ellas la de los múltiples gazapos matemáticos que localizamos en las películas (aspecto no exclusivo de ellas; el propio autor nos obsequia cada cierto tiempo en
Apenas transcurrido un año de la publicación de Aventuras Matemáticas en el Cine (Editorial Guadalmazán, octubre 2015), José María Sorando nos propone una nueva entrega enmarcada en esos dos campos tan apreciados por los lectores de esta sección, el cine y las matemáticas. En esta ocasión, se nos indica en el prólogo que el leitmotiv son algunos Desastres Matemáticos en el Cine, entendidos en un amplio sentido, tanto que el título final es Resolviendo Problemas, que a la postre constituirá el deseo del autor sobre lo que debería ser el objetivo del estudio de esta disciplina. Hasta llegar ahí, recorremos un camino jalonado por diferentes etapas, entre ellas la de los múltiples gazapos matemáticos que localizamos en las películas (aspecto no exclusivo de ellas; el propio autor nos obsequia cada cierto tiempo en 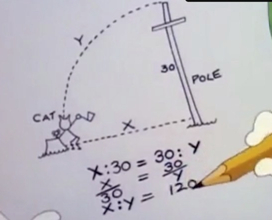 Los clasifica en distintas categorías: disparates, gazapos voluntarios, gazapos aparentes, pi-fias (ya sabéis que en Pi está todo lo publicado y publicable, teoría que también comenta; por dar una condición suficiente, este apartado podría demostrar también que Pi va a aparecer en todo libro sobre cine y matemáticas, no en vano es seguramente la constante más conocida universalmente por lo que guionistas y realizadores van a tender a incluirla allá donde necesiten algo relacionado con las matemáticas, asegurándose de este modo que el público potencial entienda el gag, la referencia o lo que se tercie. Esto garantiza que los que escribimos sobre esto siempre vamos a tener que meter a Pi con alguna nueva película), y dislates varios de la vida real, tomados a pie de calle. Finalmente para no dejar tan mal sabor de boca, se señalan tres momentos en los que los guionistas se han preocupado de hacerlo bien en tres campos matemáticos diferentes: aritmética, combinatoria y geometría.
Los clasifica en distintas categorías: disparates, gazapos voluntarios, gazapos aparentes, pi-fias (ya sabéis que en Pi está todo lo publicado y publicable, teoría que también comenta; por dar una condición suficiente, este apartado podría demostrar también que Pi va a aparecer en todo libro sobre cine y matemáticas, no en vano es seguramente la constante más conocida universalmente por lo que guionistas y realizadores van a tender a incluirla allá donde necesiten algo relacionado con las matemáticas, asegurándose de este modo que el público potencial entienda el gag, la referencia o lo que se tercie. Esto garantiza que los que escribimos sobre esto siempre vamos a tener que meter a Pi con alguna nueva película), y dislates varios de la vida real, tomados a pie de calle. Finalmente para no dejar tan mal sabor de boca, se señalan tres momentos en los que los guionistas se han preocupado de hacerlo bien en tres campos matemáticos diferentes: aritmética, combinatoria y geometría.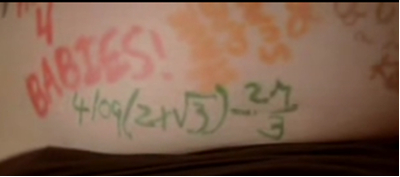 También en páginas previas, se indica acertadamente que algunos gazapos provienen de la versión doblada, no de la original. Por ello es aconsejable siempre tratar de verificar de dónde proviene el posible fallo. Y en este caso, la frase que el protagonista dice en la versión original es: “This was one of the hardest things already decided. It took me three years to do so. And I was in love for it”. No hay alusión a integral alguna por ninguna parte. El gazapo es por tanto achacable al doblaje al castellano (en el doblaje latino, en la versión estrenada en Hispanoamérica, se ha doblado así: “Esta es una de las ecuaciones más interesantes que he resuelto. Me tomó tres años”. Tampoco es una ecuación, obviamente. Puede verse en YouTube bajo el título No puedo decir adiós). Por otro lado (lo siento, las integrales y las series infinitas siempre me han gustado especialmente; raro que es uno) que una calculadora me proporcione un resultado inmediatamente, sin más que dar una tecla, no es un argumento como para parar de resolverla (puede darte pistas de su resolución, eso sí) hasta no encontrar la forma de hacerlo por uno mismo.
También en páginas previas, se indica acertadamente que algunos gazapos provienen de la versión doblada, no de la original. Por ello es aconsejable siempre tratar de verificar de dónde proviene el posible fallo. Y en este caso, la frase que el protagonista dice en la versión original es: “This was one of the hardest things already decided. It took me three years to do so. And I was in love for it”. No hay alusión a integral alguna por ninguna parte. El gazapo es por tanto achacable al doblaje al castellano (en el doblaje latino, en la versión estrenada en Hispanoamérica, se ha doblado así: “Esta es una de las ecuaciones más interesantes que he resuelto. Me tomó tres años”. Tampoco es una ecuación, obviamente. Puede verse en YouTube bajo el título No puedo decir adiós). Por otro lado (lo siento, las integrales y las series infinitas siempre me han gustado especialmente; raro que es uno) que una calculadora me proporcione un resultado inmediatamente, sin más que dar una tecla, no es un argumento como para parar de resolverla (puede darte pistas de su resolución, eso sí) hasta no encontrar la forma de hacerlo por uno mismo. El análisis de todo tipo de datos es para ello fundamental, que va desde la información más simple que en ocasiones nos dan las cifras, pasando por la que se extrae de mensajes encriptados que algunos psicópatas proporcionan sin reparo alguno (la criptografía y el análisis de frecuencias tienen mucho que decir, como en el caso del célebre asesino del zodiaco cuya descripción se detalla a partir de una de las dos recientes recreaciones cinematográficas; también se recuerdan algunos precedentes basados más o menos en ese mismo sujeto). Cuando ese análisis es más concienzudo, y se aplican procedimientos estadísticos, aparecen, por ejemplo, los mapas de probabilidad de “zonas calientes”, ampliamente difundidos en la serie Numb3rs, de la que, obviamente, se repasan varios episodios. La explicación va remitida en general a los propios guiones y diálogos. En relación a los casos planteados, se recuerdan casos similares acontecidos en nuestro país, muchas veces anteriores en el tiempo, lo que ratifica el conocido adagio de que la realidad supera la ficción. En este caso, va por delante, y a partir de ahí el trabajo de los matemáticos, analistas y estadísticos trata de hacer más difícil la tarea de los malhechores.
El análisis de todo tipo de datos es para ello fundamental, que va desde la información más simple que en ocasiones nos dan las cifras, pasando por la que se extrae de mensajes encriptados que algunos psicópatas proporcionan sin reparo alguno (la criptografía y el análisis de frecuencias tienen mucho que decir, como en el caso del célebre asesino del zodiaco cuya descripción se detalla a partir de una de las dos recientes recreaciones cinematográficas; también se recuerdan algunos precedentes basados más o menos en ese mismo sujeto). Cuando ese análisis es más concienzudo, y se aplican procedimientos estadísticos, aparecen, por ejemplo, los mapas de probabilidad de “zonas calientes”, ampliamente difundidos en la serie Numb3rs, de la que, obviamente, se repasan varios episodios. La explicación va remitida en general a los propios guiones y diálogos. En relación a los casos planteados, se recuerdan casos similares acontecidos en nuestro país, muchas veces anteriores en el tiempo, lo que ratifica el conocido adagio de que la realidad supera la ficción. En este caso, va por delante, y a partir de ahí el trabajo de los matemáticos, analistas y estadísticos trata de hacer más difícil la tarea de los malhechores.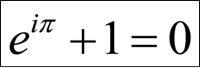 Muy interesante la historia real de Igor Tamm, y una no menos lucida reflexión sobre cómo algunos se han ido cargando el denominado estado del bienestar por su rácana aplicación de pretendidas fórmulas de austeridad. Y por supuesto no podía faltar la guinda del pastel, la calificada como fórmula más hermosa de las matemáticas por conjugar los principales “actores” de diferentes ramas de esta disciplina.
Muy interesante la historia real de Igor Tamm, y una no menos lucida reflexión sobre cómo algunos se han ido cargando el denominado estado del bienestar por su rácana aplicación de pretendidas fórmulas de austeridad. Y por supuesto no podía faltar la guinda del pastel, la calificada como fórmula más hermosa de las matemáticas por conjugar los principales “actores” de diferentes ramas de esta disciplina. A pesar de ser éste el objetivo de la enseñanza de las matemáticas, choca el escaso éxito que los alumnos suelen tener en esta tarea, y no sólo eso sino la verdadera animadversión hacia ello. Una de las causas podría ser, según el autor, la poca fortuna en el planteamiento de los ejercicios que tradicionalmente se han venido proponiendo en la escuela, puestos de manifiesto en varias escenas. Hay también referencias al grupo Bourbaki y a Piaget y la psicología en correspondencia a cómo el primer grupo organizó la estructura de las matemáticas en sus trabajos, a la regla de Laplace para calcular probabilidades, al concepto de esperanza matemática, al origen del álgebra y su aplicación en situaciones prácticas como las herencias, medidas de terrenos, transacciones comerciales, etc.
A pesar de ser éste el objetivo de la enseñanza de las matemáticas, choca el escaso éxito que los alumnos suelen tener en esta tarea, y no sólo eso sino la verdadera animadversión hacia ello. Una de las causas podría ser, según el autor, la poca fortuna en el planteamiento de los ejercicios que tradicionalmente se han venido proponiendo en la escuela, puestos de manifiesto en varias escenas. Hay también referencias al grupo Bourbaki y a Piaget y la psicología en correspondencia a cómo el primer grupo organizó la estructura de las matemáticas en sus trabajos, a la regla de Laplace para calcular probabilidades, al concepto de esperanza matemática, al origen del álgebra y su aplicación en situaciones prácticas como las herencias, medidas de terrenos, transacciones comerciales, etc.