89. (Marzo 2018) Ritmos euclídeos y ritmos equilibrados
89. (Marzo 2018) Ritmos euclídeos y ritmos equilibrados |
 |
 |
 |
| Escrito por Paco Gómez Martín (Universidad Politécnica de Madrid) |
| Miércoles 07 de Marzo de 2018 |
|
1. Ritmos equilibrados y euclídeos La representación geométrica de ritmos y escalas ha sido con frecuencia una herramienta útil para su análisis y para el descubrimiento de nuevos objetos musicales. En esta columna vamos a tratar los patrones rítmicos y de escalas llamados equilibrados y también examinaremos una herramienta, XronoMorph, diseñada por Andrew Milne y Roger Dean [MD16], que permite experimentar con esos ritmos. Para las definiciones que vamos a presentar, necesitamos previamente fijar una circunferencia en la que pondremos los objetos musicales —alturas de sonido o duraciones —. En el vídeo siguiente, A different way to visualize rhythm, John Varney habla de las ventajas de la representación geométrica del ritmo, sobre todo cuando los ritmos son cíclicos y estos se visualizan en una circunferencia.
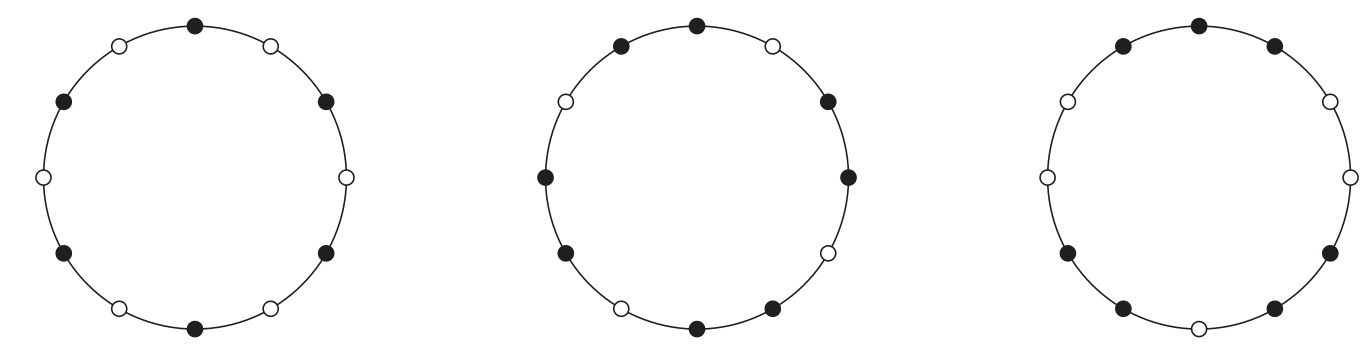
Por sencillez de la exposición, supondremos que los objetos musicales ritmos y, por tanto, los puntos en la circunferencia marcan duraciones consecutivas. El análisis es el mismo si tratamos las escalas. Un ritmo es equilibrado si el centro de gravedad es el propio centro de la circunferencia. Para hablar con propiedad del centro de gravedad, supondremos que cada nota sobre la circunferencia tiene masa unidad y entonces dicho centro es el punto de aplicación de la resultante de todas las fuerzas de gravedad dada por las notas. Por ejemplo, en la figura de abajo, los tres ritmos, dados por los círculos negros, son ritmos equilibrados; aquí se ha tomado doce como número de pulsos para los ritmos.
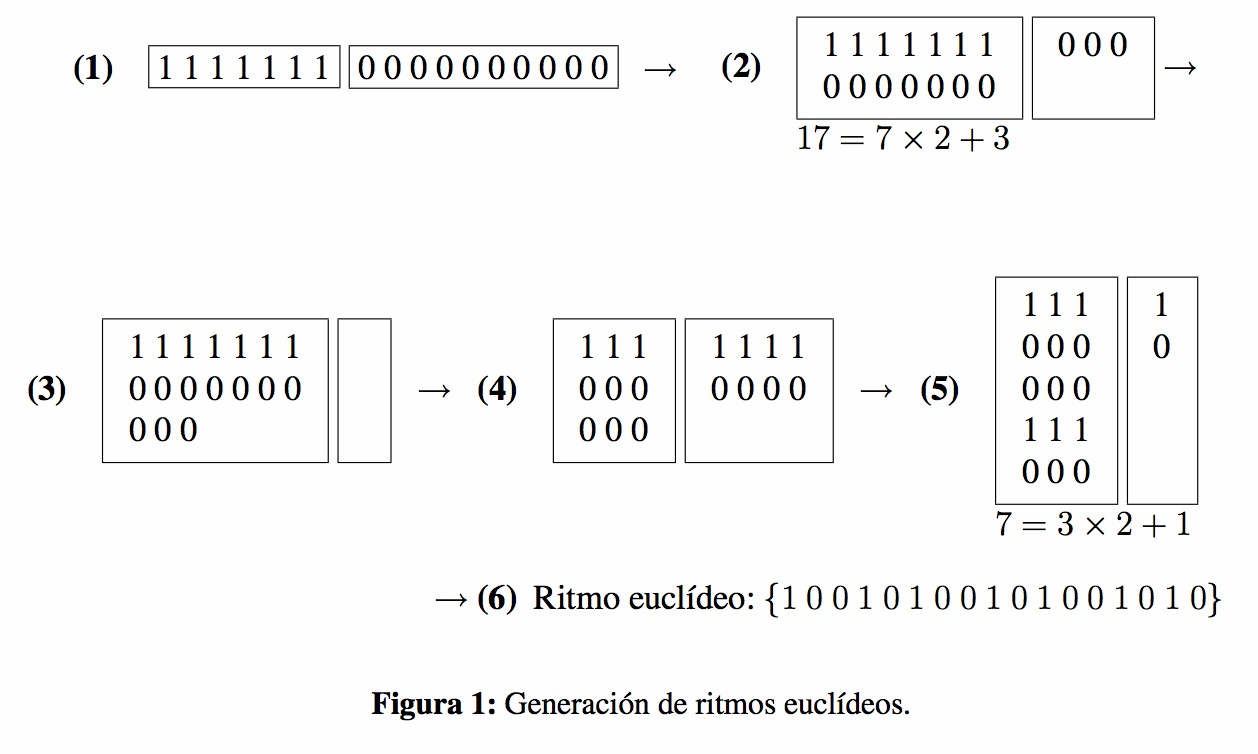
Figura 1: Ejemplos de ritmos equilibrados. El concepto de ritmo equilibrado está relacionado con el de ritmo regular. Un ritmo regular es aquel que tiene las notas distribuidas tan regularmente como sea posible a lo largo del círculo. Se sabe que los ritmos regulares solo pueden tener una o dos duraciones posibles y que estas tienen que estar colocadas en un orden especial. Se conocen varios algoritmos para generar ritmos regulares; entre ellos los más importantes son el de Bjorklund [GMTT09b], el de Clough y Douthett [CD91], o el mismísimo algoritmo de Euclides, que cuando se adapta a la formación de grupos, produce ritmos regulares. Los dos primeros ritmos de la figura 1 son regulares. En una columna anterior [Góm12], Amalgamas, aksaks y métricas euclídeas, se trataron a fondo los ritmos regulares, también llamados ritmos euclídeos. Para información más sobre los algoritmos, propiedades de los ritmos regulares y sus aplicciones en música, véanse [DGMM+09, GMTT09b, GMTT09a, CD91]. En lo que sigue usaremos tres notaciones para designar los ritmos: la notación de ceros y unos, adecuada para el tratamiento algorítmico; la notación de x y ., que es cómoda para la lectura musical; y la notación de distancia. Si no se dice nada en contra, cuando un ritmo se represente sobre el círculo, empezaremos a describirlo desde las doce del mediodía. Así, los ritmos de la figura 1, de izquierda a derecha, se designan por R1 = [101010101010 ] = [x . x .x .x .x .x ] = (222222) R2 = [101101101101] = [x .x x . x x . x x . x] = (21212121) R3 = [110011011001] = [x x ..x x . x x . .x] = (1312131) 2. Ritmos equilibrados y euclídeos 2.1. Ritmos euclídeos En lo que sigue vamos a seguir la exposición del trabajo Si Euclides lo supiese... se sentiría orgulloso [Góm09] del propio autor de estas líneas. El algoritmo de Euclides consiste en hacer divisiones sucesivas para hallar el máximo común divisor de dos números positivos (m.c.d. de aquí en adelante). Si queremos hallar el m.c.d. de dos números a y b, suponiendo que a > b, primero dividimos a entre b, y obtenemos el resto r de la división. Euclides se dio cuenta de que el m.c.d. de a y b era el mismo que el de b y r. En efecto, cuando dividimos a entre b, hallamos un cociente c y un resto r de tal manera que se cumple que: a = c⋅b + r Esta ecuación nos dice que todo divisor común de a y b tiene que serlo también de r. En particular, el m.c.d. de a y b es el m.c.d. de b y r. Por ejemplo, calculemos el máximo común de 17 y 7. Como 17 = 7 ⋅ 2 + 3, entonces el m.c.d.(17, 7) es igual al m.c.d.(7, 3). De nuevo, como 7 = 3 ⋅ 2 + 1, entonces el m.c.d.(7, 3) es igual al m.c.d.(3, 1). Aquí es claro que el m.c.d. entre 3 y 1 es simplemente 1. Por tanto, el m.c.d entre 17 y 7 es 1 también. ¿Cómo se transforma el cálculo del máximo común divisor en un método para generar patrones distribuidos con regularidad máxima? Ilustraremos el proceso con un ejemplo de ritmos. Supongamos que tenemos 17 pulsos y queremos distribuir de forma regular 7 notas entre los 17 pulsos. Sigamos los pasos dados en la figura 2. Primero, alineamos el número de notas y el número de silencios (siete unos y diez ceros); véase la figura 2-paso (1). A continuación, formamos grupos de 7, los cuales corresponden a efectuar la división de 17 entre 7; obtenemos, pues, 7 grupos formados por [1 0] (en columnas en el paso (2) de la figura 2). Sobran tres ceros, lo cual indica que en el paso siguiente formaremos grupos de 3. Tras formar el primer grupo —véase el paso (3) de la figura 2— nos quedamos sin ceros. Continuamos agrupando de 3 en 3 tomando los grupos de la otra caja, en la que quedan 4 columnas (figura 2-paso (4)). Procedemos así que queden uno o cero grupos; de nuevo, esto es equivalente a efectuar la división de 7 entre 3. En nuestro caso, queda un solo grupo y hemos terminado (paso (5)). Finalmente, el ritmo se obtiene leyendo por columnas y de izquierda a derecha la agrupación obtenida (paso (6)).
Figura 2: El algoritmo de Euclides para generar ritmos regulares.
Aquí cada 1 representa una nota [x] y cada 0, un silencio [.]. El ritmo que hemos generado con nuestra notación se escribe entonces como [x . . x . x . . x . x . . x . x .]. Los ritmos generados por este método se llaman ritmos euclídeos. El ritmo euclídeo de k notas y n pulsos se designa por E(k,n). Otra manera útil de designar un ritmo es mediante las duraciones de las notas en términos de pulsos. El ritmo euclídeo que acabamos de obtener con esta notación se escribe E(7,17) = [x . . x . x . . x . x . . x . x .]= (3232322). Demain y sus coautores [DGMM+09] probaron formalmente que este algoritmo proporciona, salvo rotaciones, la única manera de distribuir k objetos entre n del modo más regular posible. Aún más, había varios algoritmos propuestos de manera independiente y ellos probaron que, en realidad, eran todos equivalentes al viejo algoritmo de Euclides. Damos a continuación una pequeñísima muestra de ritmos euclídeos que se encuentran en las músicas tradicionales del mundo.
Existen cerca de dos centenares de ritmos de músicas del mundo documentados que son generados por el algoritmo de Euclides. De nuevo, véase el artículo The distance geometry of music de Demain y sus coautores [DGMM+09]. He aquí una lista de las principales propiedades de los ritmos regulares o ritmos euclídeos:
2.2. Ritmos equilibrados Cuando se considera el círculo donde se inscriben los ritmos, si el polígono resultante al unir las notas consecutivas del ritmo es regular, entonces el ritmo es equilibrado. De nuevo, el recíproco no es cierto, como atestiguan los polígonos de la figura de arriba. En el artículo Perfect balance: A novel principle for the construction of musical scales and meters, de Milne y coautores [MBHW15], se estudian a fondo las propiedades de los ritmos equilibrados. En dicho artículo los autores asocian a cada ritmo una serie de Fourier discreta uno de cuyos coeficientes es una medida del equilibrio del ritmo. La condición de ser equilibrado se puede pensar como la varianza circular. Si el ritmo tiene varianza cero, entonces se reduce a un único punto. En cambio, si la varianza es máxima entonces el ritmo será equilibrado; véase el artículo mencionado para los detalles técnicos. 3. XronoMorph: una aplicación para la experimentación rítmica Para terminar, querríamos comentar el programa XronoMorph. Se trata de una aplicación que permite experimentar con ritmos equilibrados y ritmos euclídeos. Es una aplicación gratis y funciona en los sistemas operativos Mac OS X y Windows. Usa como objeto centrar para la representación una circunferencia y permite describir polirritmos en términos de polígonos inscritos. Abajo tenemos un vídeo donde se ve la interfaz.
En el vídeo de abajo podemos ver un ejemplo en que varios polígonos regulares se superponen. Estos polígonos representan ritmos euclídeos y aparecen organizados en una polirritmia.
En el siguiente vídeo tenemos ritmos equilibrados que también forman una polirritmia, en este caso la superposición de un ritmo binario con uno ternario.
En este otro vídeo vemos un 3 contra 5.
Por último, XronoMorph permite varias operaciones con polígonos, como por ejemplo, la rotación. Se pueden componer polirritmias muy complicadas asignando un instrumento a cada rotación de un polígono. Véase una muestra en el siguiente vídeo.
Bibliografía [CD91] J. Clough and J. Douthett. Maximally even sets. Journal of Music Theory, 35:93–173, 1991. [DGMM+09] Erik D. Demaine, Francisco Gomez-Martin, Henk Meijer, David Rappaport, Perouz Taslakian, Godfried T. Toussaint, Terry Winograd, and David R. Wood. The distance geometry of music. Computational Geometry: Theory and Application, 42(5):429–454, 2009. [GMTT09a] F. Gomez-Martin, P. Taslakian, and G. T. Toussaint. Interlocking and euclidean rhythms. Journal of Mathematics and Music, 3(1), 2009. [GMTT09b] F. Gomez-Martin, P. Taslakian, and G. T. Toussaint. Structural properties of euclidean rhythms. Journal of Mathematics and Music, 3(1), 2009. [Góm09] Paco Gómez. Si Euclides lo supiese... se sentiría orgulloso, Noviembre, 2009. [Góm12] Paco Gómez. Amalgamas, aksaks y métricas euclídeas, Noviembre, 2012. [MBHW15] A. Milne, D. Bulger, S. Herff, and Sethares W. Perfect balance: A novel principle for the construction of musical scales and meters. In T. Collins, D. Meredith, and A. editor Volk, editors, Proceedings of the 5th International Conference on Mathematics and Computation in Music, pages 97–108. Springer, Berlin, 2015. [MD16] Andrew J. Milne and Roger T. Dean. Computational creation and morphing of multilevel rhythms by control of evenness. Computer Music Journal, 40(1):35–53, 2016. |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |