 133. SOLUCIÓN CONCURSO DEL VERANO DE 2018
133. SOLUCIÓN CONCURSO DEL VERANO DE 2018 |
 |
 |
 |
| Escrito por Alfonso Jesús Población Sáez | ||||||||||||||
| Jueves 13 de Septiembre de 2018 | ||||||||||||||
|
Una nueva edición de este concurso, en el que he vuelto a disfrutar con las ocurrentes y meritorias respuestas de los participantes. Desgranamos a continuación todas las cuestiones.
En esta ocasión pretendía que la película fuera más conocida que en años precedentes, y opté por Doctor Zhivago, la versión dirigida por el gran David Lean en 1965. No se encuentra entre mis favoritas de este director (aunque me parece muy relevante prácticamente toda su obra), pero reconozco que es, estéticamente y argumentalmente una producción excepcional, rodada como todo el mundo sabe en su mayor parte en nuestro país. Así pues, la película ha ofrecido poca dificultad a los concursantes; Cuestiones Matemáticas M – 1.- Un grupo de diez amigos quedan para ir al cine. A la vez, un grupo de otros nueve amigos van a la misma película también juntos. Catorce de esas diecinueve personas compran un cucurucho de palomitas. El coste total de la entrada a la película más el cucurucho de palomitas de maíz para uno de los dos grupos resultó ser el mismo que para el otro grupo. Si la entrada al cine costaba 6 euros, ¿cuáles son los posibles precios de las palomitas?
Todos los concursantes han respondido correctamente a esta cuestión, la más sencilla, para animar al personal. Dado que el grupo más grande necesita comprar solo un boleto más que el grupo más pequeño, la diferencia de precio para las entradas entre los grupos es de 6 €. Por tanto, el grupo más pequeño pagó 6 € más por palomitas de maíz que el grupo más grande para compensar la diferencia. Así, el grupo más pequeño debe haber comprado más de la mitad de las 14 bolsas de palomitas de maíz, por lo menos 8 bolsas. Por otro lado, como cada persona sólo puede comprar como máximo un cucurucho, por lo menos 9 bolsas. Las posibilidades del precio de las palomitas son entonces:
M – 2.- Los números 100231 y 25561 proporcionan el mismo resto, el número de largometrajes dirigidos por el realizador de la película, cuando se dividen por el año de estreno de la película que nos ocupa. ¿De qué año es la película? ¿Cuántas películas dirigió el director?
Todos los concursantes dieron la respuesta correcta, pero uno lo hizo sin explicación matemática alguna. Recordemos que en este apartado es preciso incluir una prueba. Dar simplemente la solución no sirve dado que, encontrada la película a partir de la resolución de otras cuestiones, indicar fecha de estreno y películas del director no tiene demasiado misterio ya que son datos localizables fácilmente. En este caso de los diez puntos, sólo se dan la mitad, cinco. Una forma de resolverlo, utilizando exclusivamente los datos del enunciado es la siguiente: Del enunciado del problema se deduce que, llamando x al divisor (el año de estreno de la película) e y al resto (número de películas dirigidas por el realizador), se tiene que ax + y = 100231 bx + y = 25561 Al restar ambas ecuaciones, tenemos que x(a – b) = 74670 = 2·3·5·19·131. Si multiplicamos esos factores, observamos que el único año de producción posible (el cine se descubrió en 1895 y la producción nos llega hasta 2018) es 3·5·131 = 1965. De ahí se deduce inmediatamente el número de películas del director, 16. M – 3.- Demostrar que, si un tetraedro solamente tiene un lado mayor que la unidad, entonces su volumen es menor o igual que un octavo. ¿Podría ser el ejercicio que muestra la imagen de la película?
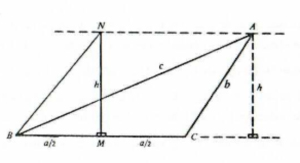
Sean A, B, C, D los vértices del tetraedro con todos los lados menores o iguales a la unidad excepto AD. Denotaremos por a, b, c los lados del triángulo ABC y h la altura de A a BC. Por el punto medio M, de BC, tracemos la perpendicular MN de longitud h (ver figura). Supongamos que A y C se encuentran al mismo lado de la recta MN. Entonces BN ≤ BA. Elevando al cuadrado la desigualdad, tenemos que
Como, por hipótesis, c ≤ 1, esto nos lleva a que h2 ≤ 1 −
Sea k la altura desde D a BC en el triángulo DBC, cuyos lados también tiene longitudes menores o iguales a la unidad. Un razonamiento análogo al anterior demuestra que k ≤
Como a ≤ 1, tenemos que
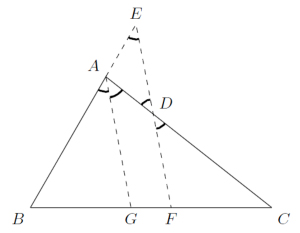
Este ejercicio era un poco más difícil. Uno de los concursantes lo dejó sin hacer y otro demostró que el volumen debería ser menor que 1/3, pero se pedía una acotación más fina. El resto lo resolvió correctamente. Sobre si podría o no ser el ejercicio que resolvia Lara, seguramente no, pero se buscó uno en el que la imagen que aparecía tuviera algún parecido con el propuesto. Desde luego algo de geometría era, pero seguramente más elemental. M – 4.- Un triángulo ABC tiene lados AB = 5, AC = 7, y BC = 8. El punto D se encuentra sobre el lado AC de modo que AB = CD. Extendamos el lado BA a partir de A hasta un punto E tal que AC = BE. La línea ED corta entonces al lado BC en el punto F. ¿Cuánto miden AD, AE, BF y FC? De nuevo pleno de aciertos en los concursantes. El ejercicio también era más sencillo. Han utilizado trigonometría elemental, o geometría analítica. Alguno lo ha resuelto ayudándose de Geogebra. Se detalla a continuación una resolución aún más elemental. Como |CD| = |AB| = 5, y |AC| = 7, |AD| = |AC| − |CD| = 2. Análogamente, |AE| = |BE| − |AB| = |AC| − |AB| = 2. Por tanto, el triángulo DAE es isósceles y ∠AED = ∠ADE = ∠CDF. Más aún, ∠BAC = 180º − ∠DAE = ∠AED + ∠ADE = 2 ∠AED.
Tracemos la bisectriz de ∠BAC, siendo G la intersección de esa bisectriz con el lado BC, como se muestra en el dibujo. El argumento utilizado anteriormente demuestra que todas las medidas de los ángulos indicados son iguales, por lo que AG || EF. Como AG y EF son paralelos, el triángulo ABG es semejante al triángulo EBF, y por tanto
Análogamente, los triángulos CAG y CDF son semejantes, de donde
Teniendo en cuenta estas proporciones, para algún valor a, tenemos que |BG| = 5a, |GF| = 2a, y |FC| = 5a. Entonces |BC| = |BG| + |GF| + |FC| = 12a. Pero como |BC| = 8, se deduce que a = 8/12 = 2/3, y por tanto, |FC| = 10/3, y |BF| = |BG| + |GF| = 14/3. M – 5.- Resolver las siguientes integrales de algún modo “no convencional”
Lo cierto es que las integrales siguen causando cierto “rechazo” entre la gente. Pero no podían faltar en una película ambientada en la Unión Soviética, no en vano, de aquel país provienen un montón de manuales con cientos de ejercicios de integrales que, antes de la difusión de software de cálculo simbólico, había que ingeniárselas para resolverlas (cuando se pedían en modo exacto, obviamente). Se pedía resolverlas mediante alguna “idea feliz” que nos simplificara los tediosos cálculos que a veces acompañan a este tipo de ejercicios. i.- Para la primera estudiamos las simetrías de las rectas y = 9 – x e y = x + 3 comprobando que se corta en x = 3, el punto medio de los extremos de la integral. Además, ambas rectas son positivas en el intervalo [2, 4]. Probemos un cambio de variable que convierta 9 – x en t + 3: 9 – x = t + 3 Eso nos lleva al cambio t = 6 – x. Con él el extremo x = 2 va a parar a t = 4, y x = 4 a t = 2. En definitiva
Obsérvese que el signo menos desaparece si intercambiamos los extremos de integración, y que ambas integrales tiene el mismo denominador. La variable de integración es irrelevante cuál sea, de modo que si sumamos ambas integrales tenemos que
Por lo que I = 1. ii.- En el caso de la segunda integral, el truco consiste en darla un nombre, por ejemplo
y sacarnos de “la chistera” otra integral “parecida”
Gracias a las propiedades de las integrales tenemos entonces que I1 + I2 = ∫dx = x + C1. Además, I1 - I2 = Resolviendo el sistema lineal, deducimos el valor de ambas (dos por el precio de una, ja ja ja). La pedida es finalmente I1 = ½ (x - ln(sen x + cos x)) + Cte. iii.- Para la última, puede escribirse sen(πx) = cos(π/2 – πx), y entonces 1 + sen(πx) = 2 cos2(π/4 – πx/2). Entonces con el cambio de variable t = π/4 – πx/2, llegamos a una integral inmediata, y deshaciendo el cambio, se tiene que
M – 6.- ¿Cuál es la probabilidad de obtener un rey, una reina y un Jack en una baraja francesa (de póker) convencional (52 cartas; sin comodines, por tanto)? Veámoslo de dos modos diferentes. La probabilidad de sacar un rey a la primera es 4/52. La probabilidad de sacar una reina después de un rey en la siguiente extracción, sin haber reemplazado la carta anterior, es 4/51. Análogamente la de sacar una sota (un Jack) la tercera es de 4/50. Por tanto, la probabilidad total (son sucesos independientes) será de Por otro lado, hay seis órdenes posibles de obtenerlos: KQJ, KJQ, QKJ, QJK, JKQ, JQK. Por tanto la probabilidad es 6 x También se puede razonar así: el número de formas de elegir tres cartas cualesquiera del mazo de 52 es
En el caso de las cuestiones de cálculo de probabilidades, siempre surgen dudas respecto a qué se pregunta en realidad. A pesar de que la propia naturaleza del concurso incluye algún tipo de interpretación para dar un poco de juego en cuanto a qué demonios se quiere decir con esto o aquello, lo cierto es que, en este caso, yo creo que estaba totalmente claro, pero os agradezco las puntualizaciones a la hora de mejorar en lo posible los enunciados. Excepto dos personas, el resto interpretó correctamente lo que se pedía. M – 7.- ¿Y la probabilidad de extraer el rey, habiendo extraído previamente la reina y la sota?
Típico ejercicio de probabilidad condicionada, aunque también podemos razonar de un modo más directo: se han extraído ya dos cartas que no se han reemplazado (quedan por tanto 50 en el mazo), y queremos calcular la probabilidad de obtener un rey en la siguiente extracción (no ha salido ninguno, por lo que hay 4). La probabilidad pedida es entonces 4/50 = 2/25 ≈ 0.08
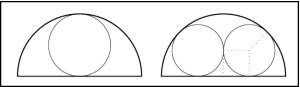
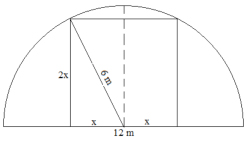
M – 8.- ¿Qué opción es mejor teniendo en cuenta que deseamos que, en caso necesario, se desagüe la mayor cantidad de agua posible lo más rápidamente posible? ¿Qué tamaño de tubería se debería usar?
La imagen muestra las dos opciones que plantea el ejercicio. Si utilizáramos una única tubería, su radio sería, como máximo, de 3 metros (la sección tiene de anchura 12 m.; como es semicircular, la altura será de 6 m., y tratamos de meter una tubería circular lo más grande posible). El área de la sección de la tubería sería por tanto de 9π m2. Si utilizáramos dos tuberías de radio r, la longitud del cuadrado punteado de la imagen sería r. Utilizando el teorema de Pitágoras, la diagonal del cuadrado sería r = 6/( La superficie de las dos tuberías tendría por tanto área 2π r2 = 2π (6 Por tanto, dos tuberías aliviarían mayor cantidad de agua. M – 9.- ¿Y si optan en vez de tuberías por una cámara de sección cuadrada?
La situación es la planteada en la imagen, sólo debemos calcular las dimensiones del cuadrado en cuestión. Aplicando el teorema de Pitágoras, se tiene que 62 = x2 + (2x)2, y de ahí la raíz positiva
El lado del cuadrado inscrito será entonces En definitiva, un poco más que una sola tubería circular, pero menos que dos circulares.
M – 10.- Si finalmente fuera rectangular, ¿cuál serían las dimensiones de superficie máxima? Se trata de un problema clásico de optimización, de cálculo de máximos. En este caso, denotando por x como en M – 9 a la mitad de la base del rectángulo, e y a su altura (de la ecuación de la circunferencia se sigue que esa altura es f(x) = 2x Del análisis elemental se sabe que toda función continua alcanza el máximo y mínimo absolutos en un intervalo cerrado. En este caso nos interesa el valor máximo. Derivamos la función e igualamos el resultado a cero para obtener los puntos críticos. Esto nos da los valores x = 3 Para deducir cuál es el máximo y el mínimo absolutos no hace falta ir a la derivada segunda en este caso ya que el citado teorema de Weierstrass nos asegura que los extremos absolutos se encuentran entre los valores obtenidos y los extremos del intervalo (al ser éste cerrado y acotado). Hay además un valor para el que la derivada primera no existe, x = 6, pero es un caso extremo en el que la función se anula, así que nos permitiremos la licencia de “pasar de él” de acuerdo con el ejercicio que nos ocupa. Así, se tiene que f(0) = f(6) = 0, f(3 de modo que el máximo absoluto se alcanza para x = 3 Uno de los participantes, Ingeniero de Caminos, Canales y Puertos, experto por tanto en este tipo de cuestiones, nos dejó una estupenda descripción desde el punto de vista de la Física de este tipo de problemas de desagües: “El caudal que desagua una conducción es el producto de la velocidad del fluido y de la sección de la tubería, Q = V ∙ S. Dicho esto, cuando el desagüe es en “lámina libre” o sea, la tubería no entra en presión (funcionamiento que es bastante más complejo de formular) y también en régimen laminar (que sería como decir que las gotas de agua van ordenaditas sin formar remolinos), la velocidad del fluido viene gobernada por la fórmula de Manning, la cual, a igualdad de otros parámetros (pendiente de la conducción, material, rugosidad, etc.) depende de una magnitud que se llama radio hidráulico y que se calcula del modo siguiente: Rh = A / P, donde Rh = radio hidráulico de la sección. A = área mojada (área de la sección de agua) Este parámetro, Rh, es un factor en la fórmula de Manning y tiene exponente 2/3”. Muchas Gracias por esta ampliación. Este es uno de los objetivos del juego: todos disfrutamos y todos aprendemos un poco más. M – 11.- ¿Qué cantidad de hombres y mujeres proporcionan el mayor rendimiento de acuerdo a los datos facilitados? ¿Es un buen plan, o con la mano de obra indicada podríamos tener un rendimiento mayor? Describe tal procedimiento, si lo encuentras.
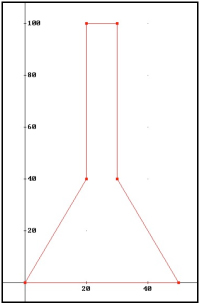
Maximizar el rendimiento z = 2x + y Sujeto a las condiciones y < 2x, si x < 20 y = 100, si 20 ≤ x ≤ 30 y + 2x < 100, si x ³ 30 0 ≤ x ≤ 50, 0 ≤ y ≤ 100 Al representar gráficamente esas condiciones, se obtiene la región factible que aparece en la imagen (que es el objeto oculto del que se habla en la cuestión C – 13, una balalaika). La resolución de estos ejercicios es a través del vector gradiente de la función objetivo z, en este caso el vector (2, 1). Gráficamente el mayor crecimiento se da a lo largo de todo el segmento 100 – 2x, 30 ≤ x ≤ 50 (óptimo múltiple). Siendo z = f(x, y) = 2x + y, f(x, 100 – 2x) = 100, con 30 ≤ x ≤ 50 El jefe de la central, Yevgraf, se las apaña mediante este procedimiento para que el rendimiento descienda lo menos posible en ausencia de mano de obra masculina. El rendimiento en los diferentes casos quedaría entonces así:
En efecto, hay mejores apaños, pero entre su prepotencia y que quería que apareciera la balalaika, esto fue lo mejor que se ocurrió, ja ja ja. M – 12.- Esa noche logra reunir ocho trozos de madera, iguales en longitud cuatro a cuatro, la mitad de ellos el doble de largos. Con ellos podría construir dos cuadrados perfectos, uno el doble del otro. Pero, ¿podría colocarlos de manera que encerraran tres cuadrados exactamente iguales? ¿Cómo?
M – 13.- Algunas cuestiones acerca de la cruz griega para resolver: i.- Cortarla en cuatro trozos con los que componer un cuadrado perfecto. De nuevo la figura adjunta nos indica un modo de hacerlo.
iv.- En tiempos de guerra escasea todo. Se necesitan brazaletes para las enfermeras con una cruz roja, pero sin desperdiciar la poca tela roja de la que disponen. ¿Cómo cortar una pieza cuadrada de modo que logremos tener dos Cruces Rojas exactamente iguales sin ninguna pérdida de tela?
v.- ¿Y si quisiéramos que las cruces resultaran de diferente tamaño?
En este caso la cruz central es de una sola pieza, y la otra se forma con los otros cuatro trozos que sobran. Cuestiones de tipo cultural C – 1.- Dos ejemplos de películas en las que el color sea decisivo, explicando brevemente por qué. Las respuestas de los concursantes han sido las siguientes: Sin City, ciudad del pecado (Robert Rodriguez, EE. UU., 2005) y Sin City: Una dama por la que matar (Sin City: A Dame to Kill For, Robert Rodriguez, EE. UU., 2014) en las que, solo aparecen algunos colores primordiales, como el rojo para destacar algunos elementos sobre otros; Sweeney Todd: El barbero diabólico de la calle Fleet (Sweeney Todd: The Demon Barber of Fleet Street, Tim Burton, EE. UU., 2008), donde se juega con los colores vivos y los colores grises para denotar escenas tristes o alegres, jugando también con la belleza y el degradado, lo limpio y lo sucio; Chocolat (Lasse Hallström, Reino Unido, 2000) donde al inicio se nos presenta un pequeño pueblo donde reina una sociedad cerrada e intolerante, en colores oscuros (grises, negros, azules). Después llegan al pueblo una mujer y su hija, calzando unos zapatos rojos trasgresores. El film se va trasformando en colores y al final hay una fiesta iluminada por un inmenso colorido síntoma del cambio ocurrido en la sociedad; American Beauty (Sam Mendes, EE. UU., 1999) que representa la vida de una familia aburrida y rutinaria, en colores grises. De pronto aparece el color rojo de las rosas y de la sangre, indicativo de pasión y muerte; En Grease (Randal Kleiser, EE. UU., 1978), la gama de colores del vestuario de la protagonista va cambiando de acuerdo a la evolución del personaje. Asimismo, el de otros intérpretes de acuerdo a lo que pretendan transmitir, bien a los demás, bien al espectador; En La Lista de Schindler (Schindler's List, Steven Spielberg, EE. UU., 1993), película a blanco y negro, el color refleja un estremecedor simbolismo en el abrigo rojo de una niña y el color de unas velas; En Alicia en el país de las maravillas (Alice in Wonderland, Tim Burton, EE. UU. 2010), los personajes principales tienen sus propios colores según lo que transmitan: Alicia el azul (frescura, libertad, verdad), el Sombrerero Loco el naranja (optimismo, diversión, entusiasmo, exaltación) y la reina el rojo (autoridad, impulsividad, agresividad, peligro). En El Pianista (The Pianist, Roman Polanski, Reino Unido, 2002) los colores grises y fríos evocan el horror del Holocausto; Del Rosa al Amarillo (Manuel Summers, España, 1963) rodada en blanco y negro separa las dos historias de amor con los dos colores, que sirven para representar dos etapas distintas de la vida, la adolescencia y la vejez; En Tres colores: azul (Trois couleurs:Bleu, Krzysztof Kieslowski, Francia, 1993) el azul trata de representar la libertad con una mujer como protagonista, y se usa magistralmente en multitud de escenas.
Yo, por mi parte, cuando pensé en la cuestión, tenía en mi cabeza títulos más clásicos (uno ya se va haciendo mayor, qué le vamos a hacer): El retrato de Dorian Gray (The Picture of Dorian Gray, Albert Lewin, EE. UU., 1945) rodada a blanco y negro salvo la aparición final, impactante, del cuadro; y El mago de Oz (The Wizard of Oz, Victor Fleming, EE. UU., 1939), en el que contrasta la vistosidad de Oz (a todo color), con la apatía de Kansas, donde vive Dorothy en blanco y negro.
C – 2.- Dos películas en las que, si no se ven en pantalla grande, no te enteras de nada, de dos décadas distintas y de dos nacionalidades diferentes. Los concursantes han propuesto, con bastante acierto (juzgue el lector las elecciones), las siguientes: muchas de ellas por la espectacularidad de los paisajes, vestuario, juegos de luces, la música escuchada con un equipo en condiciones, etc., como en El bueno, el feo y el malo (Il buono, il brutto, il cattivo; Sergio Leone; Italia; 1966), El correo del zar (Strogoff, Eriprando Visconti, Francia 1970), Nacida libre (Born free, James Hill, Reino Unido, 1966), Barry Lyndon (Stanley Kubrick, Reino Unido, 1975), Ran (Akira Kurosawa, Japón, 1985), La misión (The Mission, Roland Joffé, Reino Unido, 1986), Titanic (James Cameron, EE. UU., 1997), Memorias de África (Out of Africa, Sydney Pollack, EE. UU., 1985) y 2001, una odisea del espacio (2001: A Space Odyssey, Stanley Kubrick, Reino Unido, 1968), Handia (Jon Garaño y Aitor Arregi, España, 2017), Cleopatra (Joseph L. Mankiewicz, EE. UU., 1963), Los amantes del círculo Polar (Julio Médem, España, 1998). En otras ocasiones, el 3D, como en Spy Kids 3-D: Game Over (Robert Rodriguez, EE. UU, 2003) o Avatar (James Cameron, EE. UU., 2009), hace que la pantalla grande sea, hoy por hoy, casi la única opción. C – 3.- Dos ejemplos de salas de cine de tu ciudad que hayan desaparecido, dando algún dato, y anuncio de alguna película programada allí, publicada en algún periódico. Si fuera el caso, indicar algún dato evocador y nostálgico de esa sala.
Una pregunta para el recuerdo. Los concursantes nos recordaron salas en
En Valladolid, las salas desaparecidas desde los años 70 del siglo pasado (hubo más anteriormente) han sido muchas: Cines Alameda, Avenida, Babón, Capitol, Castilla, Cervantes (reconvertido en la actualidad en teatro), Coca, Delicias, Embajadores, Goya, Groucho, Lafuente (después Manteria-Renoir), Matallana, Parquesol Plaza, Roxy, Rex, La Rubia, Vistarama, y los teatros que han pasado a ser únicamente eso, teatros, o están cerrados (Calderón, Carrión, Lope de Vega, Zorrilla) e incluso alguno demolido (Teatro Pradera). El fenómeno de las multisalas en centros comerciales no nos ha dejado sin cines, pero supeditados al desplazamiento en automóvil. Sólo sobreviven tres héroes en el centro de la ciudad (Broadway, Casablanca y Manhattan). C – 4.- Dos películas con transiciones, describiendo brevemente las escenas en las que suceden. Esta cuestión ha costado un poco más, y eso que en realidad no había que irse muy lejos (otras películas de David Lean, como ha propuesto algún concursante). A los que no han detallado las escenas concretas se les ha dado una puntuación menor que 10. Sus propuestas han sido: En Lawrence de Arabia (David Lean, Reino Unido, 1962) el sonido del flash se enlaza con el sonido del jinete que se acerca, un golpe sobre un carro de combate se enlaza con la orden de partida de otro carro de combate en otro lugar; etc. En El Puente sobre el río Kwai (David Lean, Reino Unido, 1957) el sonido de los prisioneros bañándose se contrapone con el sonido de grillos para los que están encerrados en la celda de castigo. En Superman (Richard Donner, Reino Unido, 1978) el protagonista patea furiosamente una pelota de fútbol americano y el sonido se transforma en el pitido de un tren, el mismo tren que lleva a sus amigos y que él adelanta para estupefacción de todos ellos. En Titanic (James Cameron, EE. UU., 1997) hay muchas escenas de este tipo, por ejemplo, una orden del capitán se traslada al rugido sordo de la hélice, en el viento que sopla en la proa y en el suave murmullo de agua que rompe contra la proa del barco. En Apocalypse Now (Francis Ford Coppola, EE. UU., 1979) se ve y oye un helicóptero que cambia a un ventilador. En 39 escalones (The 39 Steps, Alfred Hitchcock, Reino Unido, 1935) se pasa del rostro de una portera gritando al chirriante silbido de una locomotora saliendo del túnel. C – 5.- Las tres pasiones del protagonista
Esta era una cuestión de “control” para asegurarme que los participantes vieran la película. La cuestión se refiere a las pasiones del personaje protagonista, Yuri, y algún concursante lo ha tomado como pasiones de Omar Sharif, el actor. Como quiera que la pregunta podía dar lugar a confusión, ambas posibilidades se han dado como válidas. Las tres pasiones de Yuri serían la poesía, la medicina y, por supuesto, Lara (Julie Christie). Las que se han señalado de Omar Sharif han sido el juego (sobre todo el bridge), las mujeres hermosas y los caballos (en efecto así lo indicó en alguna entrevista). C – 6.- Dos obras literarias, que fueran prohibidas en el país de su autor, señalando brevemente los motivos.
En esta pregunta los concursantes se han explayado aportando un montón de obras. La prohibición o censura de libros dice más bien poco a favor de unos gobiernos que deberían haberse dedicado a gobernar mejor. Listamos algunas (todas ellas absolutamente recomendables, por cierto):
C – 7.- ¿Qué actores se barajaron antes del definitivo para realizar la película-enigma de este año? El actor Peter O'Toole, protagonista de Lawrence de Arabia, fue la elección original de David Lean para Yuri Zhivago, pero declinó el papel; Max von Sydow y Paul Newman también fueron considerados. Michael Caine cuenta en su autobiografía que también participó en las pruebas de pantalla con Julie Christie, pero (después de ver los resultados con David Lean) fue quien sugirió a Omar Sharif. Siendo estos cuatro los consignados en la literatura cinematográfica, quien haya indicado menos, se le ha asignado la parte proporcional (redondeada para no incluir decimales; o sea 8 para el que cite tres, 5 para dos, 3 para uno).
C – 8.- ¿Quién es la mujer de la imagen? Señala alguna película en la que participara, y si en alguna ocasión trabajó junto a su esposo.
Siendo ocho tópicos (el nombre y siete películas), como anteriormente, se puntuó la parte proporcional en caso de dar menos (en este caso, 0, 2, 3, 4, 5, 7, 8, 9, 10, respectivamente). C – 9.- ¿Personaje con gusto por las ciencias exactas de la novela? ¿Por qué decimos que resucita? ¿Qué otro personaje, no presente en la película, tiene amplios conocimientos de matemáticas? Se trata de Pavel Ferapoitovich, es decir, Pasha Antipov. Este personaje retoma su pasión por las matemáticas cuando vive en Yuriati, un lugar cerca de los Urales. Se hace referencia a su resurrección debido a que es dado por muerto durante su periodo de servicio como subteniente, atestiguando uno de sus compañeros que le había visto siendo alcanzado por una granada, pero en realidad había sido capturado y hecho prisionero por el enemigo. Tiempo después de aquello consigue escapar y a su vez se cambia el nombre, Strielnikov. Como particularidad, casi al final de la historia se vuelve a decir que ha muerto, pero vuelve a reaparecer. En la novela hay varios personajes con amplios conocimientos de matemáticas, como Nikolai Nikolaevich, que mantiene una conversación profunda al principio de la novela con otra persona, o Shura Schlesinger, que, aunque era teósofa, conocía el rito ortodoxo, las matemáticas, las artes mágicas de la India... C – 10.- Frases semejantes en películas diferentes. ¿Qué tienen en común además esas películas?
Gran parte de ambas películas fueron rodadas en España (en la Comunidad de Castilla y León por concretar más): en Burgos (El bueno, el feo y el malo), y en Soria (Doctor Zhivago). Esta fue la idea, pero los concursantes han añadido nuevas facetas comunes correctas: la presencia en el rodaje de una locomotora de vapor Baldwin, o incluir dos de las melodías más célebres de la historia del cine. ¡¡Bravo!! Cómo afináis.
C – 11.- ¿Qué otra improvisación no esperada ni escrita tuvo lugar entre Rod Steiger y Julie Christie en el rodaje de esta misma película?
Después del baile, en el carruaje en que se desplazan, debían darse un beso. Tras dos tomas, el director no quedaba satisfecho con la escena, y en una nueva toma, Steiger decidió darle a la actriz “un beso con lengua”, lo que evidentemente la sorprendió y cabreó, como así aparece en el forcejeo posterior, que quedó tal cual para la posteridad en la película. C – 12.- ¿Qué otra célebre película se rodó en esa central hidroeléctrica?
Se trata de la presa de Aldeadávila de la Ribera, en Salamanca, en la que se rodó también el impactante desenlace de La cabina (Antonio Mercero, España, 1972) C – 13.- Objeto oculto en algún lugar presente a lo largo de toda la película, muy querido por su protagonista. ¿Cuál es? ¿Qué importancia tiene en el argumento? Una balalaika. Es el hilo conductor que nos indica los miembros de la saga: madre de Zhivago, Zhivago y su hija. Además, es el instrumento primordial del tema sonoro de la película.
Puntuaciones de los Concursantes Como cada año, me lo he pasado genial viendo como las distancias entre los participantes se reducían, cambiaban, se acercaban, según iba metiendo los datos en la hoja de cálculo. Mi más sincera enhorabuena a tod@s. El resultado final es el que veis. Uno de los participantes me ha sugerido que detallara la puntuación en las preguntas de matemáticas (en rojo), y las de tipo cultural (en azul), y lo cierto es que es curioso que el ganador haya obtenido idéntica puntuación en uno y otro lado. Curiosidades de las cifras. Francisco Pi Martínez ............... 236 (118 + 118) Marta Pérez Ceballos ............... 234 (112 + 122) Pablo Palacio Puente ............... 231 (119 + 112) Paz Jiménez Seral ................... 217 (118 + 99) Celso de Frutos de Nicolás ......... 155 (81 + 74) Alberto Gustavo Colomo ............ 142 (35 + 107) Sobre todo, esperamos que hayáis pasado un buen rato, y reiteramos nuestra enhorabuena por vuestras respuestas, algunas de verdadero mérito; y también a aquellos que lo han intentado y finalmente no se han animado a mandar nada, que seguro que los ha habido.
En esta ocasión, la RSME (Real Sociedad Matemática Española) nos ha facilitado tres títulos de la Biblioteca Estímulos Matemáticos (colaboración de la RSME y la editorial SM) para los tres primeros clasificados. Son Círculos Matemáticos; Lilavati. Matemática en verso del siglo XII; y Gardner para aficionados. En unos días recibiréis un correo electrónico para que nos facilitéis una dirección postal a la que enviároslos. Muchas Gracias por vuestra participación (bienvenidos los que participarais por primera vez, espero que os haya gustado y emocionado por los que mantenéis vuestra fidelidad desde hace años). Hasta la próxima (pero seguid la sección, que está presente todo el año, cada mes con una reseña nueva, y también con página en Facebook y Twitter, con contenidos breves, imágenes de películas fundamentalmente, cada poco tiempo). Esta dirección electrónica esta protegida contra spambots. Es necesario activar Javascript para visualizarla |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |







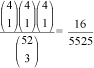
 En este caso se trataba de resolver un ejercicio de programación lineal. Denotamos por x el número de hombres e y el número de mujeres. Modelizando las condiciones que se dan en el enunciado resulta la siguiente situación
En este caso se trataba de resolver un ejercicio de programación lineal. Denotamos por x el número de hombres e y el número de mujeres. Modelizando las condiciones que se dan en el enunciado resulta la siguiente situación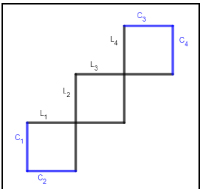 Cuestión tipo rompecabezas. La imagen adjunta nos indica cómo conseguirlo (los lados del cuadrado grande van de negro, y los del cuadrado pequeño, de azul; imagen enviada por uno de los concursantes). No se han dado por válidas aquellas soluciones en las que sobrara algún lado de cualquier cuadrado, o quedara algún cuadrado de los tres que se pedían sin algún lado.
Cuestión tipo rompecabezas. La imagen adjunta nos indica cómo conseguirlo (los lados del cuadrado grande van de negro, y los del cuadrado pequeño, de azul; imagen enviada por uno de los concursantes). No se han dado por válidas aquellas soluciones en las que sobrara algún lado de cualquier cuadrado, o quedara algún cuadrado de los tres que se pedían sin algún lado.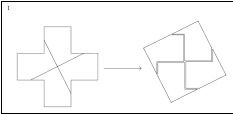 Hay infinitas formas de cortar una cruz griega con ese resultado porque dos cortes rectos cualesquiera que sean paralelos a los mostrados en la imagen adjunta que nos envió uno de los concursantes, se recolocan siempre en un cuadrado perfecto. Este apartado lo resolvieron todos los participantes.
Hay infinitas formas de cortar una cruz griega con ese resultado porque dos cortes rectos cualesquiera que sean paralelos a los mostrados en la imagen adjunta que nos envió uno de los concursantes, se recolocan siempre en un cuadrado perfecto. Este apartado lo resolvieron todos los participantes.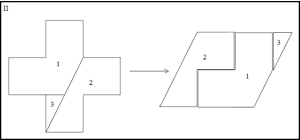 ii.- Cortarla en tres trozos con los que hacer un romboide.
ii.- Cortarla en tres trozos con los que hacer un romboide.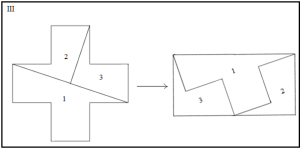 iii.- Cortarla en tres trozos con los que se pueda componer un rectángulo de base el doble de su altura.
iii.- Cortarla en tres trozos con los que se pueda componer un rectángulo de base el doble de su altura.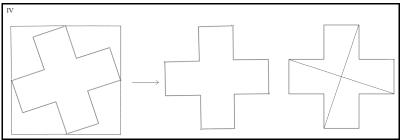
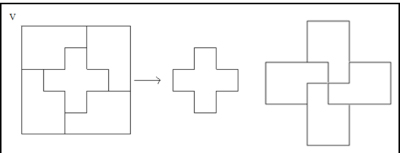
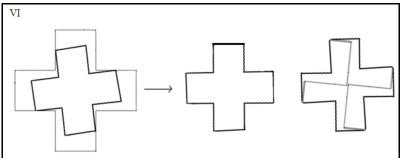 vi.- Cortar una Cruz Roja en cinco partes que formen dos Cruces Rojas más pequeñas, pero del mismo tamaño.
vi.- Cortar una Cruz Roja en cinco partes que formen dos Cruces Rojas más pequeñas, pero del mismo tamaño. Se trata de la actriz Faten Hamama (1931 – 2015), actriz, guionista y productora egipcia, primera esposa del actor Omar Sharif. Participó junto a Omar en las películas siguientes:
Se trata de la actriz Faten Hamama (1931 – 2015), actriz, guionista y productora egipcia, primera esposa del actor Omar Sharif. Participó junto a Omar en las películas siguientes:


