 135. La maravillosa Sra. Maisel (PdM V)
135. La maravillosa Sra. Maisel (PdM V) |
 |
 |
 |
| Escrito por Alfonso Jesús Población Sáez |
| Miércoles 07 de Noviembre de 2018 |
|
Hace apenas unos días se anunció el estreno de la segunda temporada de la serie triunfadora en los pasados Emmy, La maravillosa Sra. Maisel. La primera temporada se ha podido ver en España, y en uno de sus capítulos tenemos algo que comentar, matemáticamente hablando, por supuesto, además de volver a tirar de las orejas a los traductores una vez más.
Ficha Técnica: Título: La maravillosa Sra. Maisel. Título Original: The Marvelous Mrs. Maisel. Nacionalidad: EE. UU., 2017. Dirección: Amy Sherman-Palladino (9 episodios, concretamente el que nos ocupa). Guion: Amy Sherman-Palladino, creadora de la serie. Fotografía: Eric Moynier y M. David Mullen, en Color. Montaje: Kate Sanford, Tim Streeto y Brian A. Kates. Música: Eric Gorfain y Sam Phillips. Producción: Dhana Gilbert. Duración: Episodios de 57 min., aproximadamente. Ficha artística: Intérpretes (se citan sólo los que han aparecido en más episodios hasta el momento): Matilda Szydagis (Zelda, 13 episodios), Rachel Brosnahan (Miriam 'Midge' Maisel, 9 episodios), Alex Borstein (Susie Myerson, 9 episodios) Michael Zegen (Joel Maisel, 9 episodios), Marin Hinkle (Rose Weissman, 9 episodios), Tony Shalhoub (Abe Weissman, 9 episodios). Hace escasamente unos días (el 25 de octubre) se anunció el estreno de la segunda temporada de esta serie (será el 5 de diciembre en España) que arrasó en todas las categorías de comedia de los premios de televisión de los Globos de Oro (se llevó dos, a la mejor comedia y a la mejor actriz), ocho premios Emmy (mejor comedia del año, mejor guion, mejor dirección, mejor actriz cómica protagonista, mejor actriz cómica secundaria, mejor casting, mejor montaje, mejor dirección musical). En total ha conseguido hasta el momento 24 galardones y otras 23 nominaciones sin premio. Toda una revelación a pesar de la escasa publicidad que se la ha dado en general. Se trata de una serie de Amazon Prime Video (quizá sea ésta una de las razones por las que ha pasado de puntillas, por la escasa promoción que esta plataforma hace de sus productos, o que estamos todos ya un poco saturados con los anuncios de tantas cadenas y no hacemos demasiado caso), y se puede encontrar en el catálogo en español de esta plataforma. O quizá porque inicialmente su argumento no llama demasiado la atención. Cuenta los desvelos de la joven Miriam Maisel (la suelen llamar por el diminutivo apocopado Midge), una chica judía en el Manhattan de los años 50 del pasado siglo, cuya vida parecía planificada desde que nació: ir a la universidad, casarse, tener hijos, respetar los ritos de su religión, organizar las fiestas de su entorno de amigos y familiares, etc. Casi sin darse cuenta, se encuentra exactamente donde tenía que estar, viviendo feliz con su esposo y sus dos hijos en el Upper West Side. Pero, inesperadamente, su vida perfecta se vuelve del revés cuando su esposo la deja por otra mujer. Completamente descolocada, Midge no tiene más remedio que volver a evaluar qué hacer con su vida. Por casualidad, se encuentra en el escenario de un local en el que se hacen monólogos, descubriendo que tiene una habilidad especial para la comedia y decide utilizar este nuevo talento para reconstruir una vida diferente. La serie rastreará la trayectoria de Midge a medida que avanza en su carrera. Qué tiene de especial No hay más que ver unos minutos de algún capítulo para engancharse definitivamente a la serie. Los diálogos, frescos, ocurrentes, llenos de ironía y doble sentido, son muy ágiles y divertidos, muy característicos de la guionista Amy Sherman, co-creadora de la serie junto a su marido Daniel Palladino (si alguien ha visto Las chicas Gilmore, reconocerá inmediatamente el estilo). Además, el modo de poner en escena y narrar las situaciones es muy destacable. Y los temas que aborda son bastante actuales, sobre todo el papel social de la mujer. Les resultará difícil mantener el nivel de la primera temporada. Por otro lado, el elenco de actores, sobre todo la protagonista principal, es insuperable. Inmediatamente uno se siente identificado con alguno, y sobre todo con Midge. También se han cuidado mucho otros detalles de producción como el vestuario, la puesta en escena, la iluminación, la escenografía, el maquillaje. Sin esta minuciosidad, una serie de época, no resultaría convincente. Se agradece por otra parte que no haya que tragarse 120 capítulos (bueno, esto aún está por ver; money is money) para disfrutar de una serie. De momento ocho, y los que nos esperan para esta nueva temporada. Las matemáticas
Resulta que el padre de Midge, Abe Weissman, es profesor universitario de matemáticas (por eso hemos añadido al título de esta reseña lo de PdM, que para quien no lo recuerde o no nos siga habitualmente indica una serie de películas/series en las que el Profesor de Matemáticas tiene un protagonismo relevante). En la imagen lo vemos dirigiéndose al aula donde imparte docencia, en la primera aparición del personaje en su actividad laboral. Lo saludan alumnos, bedeles, incluso un alumno le abre la puerta para que entre, pero él no dice una sola palabra a nadie. No altera su expresión y continúa mirando al frente con gesto serio, muy serio. Avanza con paso firme, no se detiene ni titubea en ningún momento. Esta breve aparición nos define perfectamente cómo es. En el segundo episodio nos lo encontramos impartiendo clase. El tema es independencia lineal, vectores dependientes concretamente. Repasemos la escena:
Profesor: Ahí está. Estudiadla (observamos en la pizarra la definición de vectores linealmente dependientes: “Dos vectores v1 y v2 son linealmente dependientes si un vector es un múltiplo del otro”. Como se ve en la siguiente imagen, pone como ejemplo v1 = (1, 2, 4) y v2 = (1/2, 1, 2), y los coloca en una matriz). Bien. Esta matriz está compuesta por dos filas de vectores, v1 y v2, pero el rango es sólo uno. ¿Alguno me dice por qué? Todos los alumnos de la clase levantan la mano. El profesor va descartando uno a uno: Profesor: No, no, no, no, no. Truman. Truman: Porque una vez resuelto el primer nivel, sólo queda un vector independiente. Profesor: Correcto. Bien. ¿Alguien puede hablarme de la nulidad de esta matriz? Vuelve a levantar la mano el total de los alumnos presentes. Profesor: No, no, no, no, no. Truman. Alumno 1 (en bajo): Increíble. Profesor: Disculpa. ¿Tienes algo que comentar? Alumno 1: Nunca me pregunta a mí. Ni a ninguno de nosotros. Solamente a Truman.
Profesor: Truman sabe las respuestas. Siempre sabe las respuestas. Alumno 1: Pero nosotros podríamos saberla. Profesor: ¿En serio? ¿La sabes? Alumno: No. Profesor (a otro alumno): ¿Tú sabes la respuesta? Alumno 2: No. Profesor (a otro diferente): ¿Tú la sabes? Alumno 3: No. Profesor: No. Bien. Nadie sabe la respuesta. Sólo Truman. Alumno 1: Pero podríamos saberla. Esa es la cuestión. Profesor: ¿Podríais? ¡Podríais! Charlie, el podría no cuenta. El tal vez no cuenta. A ver si acierto no cuenta. Comentario Desde luego el razonamiento del profesor Weissman acerca de por qué siempre pregunta al mismo alumno no deja de tener su lógica, aunque tal y como indica el alumno no es demasiado edificante, didácticamente hablando. Pero es que Abe es un tipo bastante particular, también en su vida diaria. Su forma de enseñar podría resultar también llamativa, aunque no lo es tanto ya que somos muchos los que de vez en cuando tenemos que “captar” la atención de los alumnos que suelen estar más a otra cosa, o medio dormidos si es una hora propicia para ello, y “teatralizar” un poco nuestras clases. Sin embargo, la respuesta a porqué el rango de la matriz
es uno que da el “aplicado” Truman, es un poco “rara”. Recordémosla: Porque una vez resuelto el primer nivel, sólo queda un vector independiente. ¿Qué es eso del primer nivel? Soy licenciado en matemáticas, ¿me he perdido algo en estos años? ¿Se refiere a la primera fila? ¿Al primer elemento de la matriz? ¿De qué nivel se habla? Como tantas otras veces, la respuesta la tenemos en las lamentables traducciones que se hacen para los doblajes al castellano en asuntos que tiene que ver con materias técnicas (¡¡ya hemos comentado esto en muchas ocasiones, tanto desde esta sección como otros compañeros!! Y ya hemos razonado porqué deberían molestarse en hacer las cosas correctamente, pero bueno, será que nadie nos lee, o a nadie le importan estos “detallitos sin importancia”. Luego que las notas de los ciudadanos en ciencias son malas, o nos reímos de los disparates que se sueltan). Sin más dilación, vayamos a la versión original (¡¡a lo mejor el fallo viene de origen!!). Pues bien, Truman dice esto: Because once it's reduced to echelon form, there's only one independent vector ¿Hace falta que lo comente? Venga sí, dedicándoselo (¡¡con cariño!!) al “eminente” traductor responsable del tema (¡¡por favor, que llegue a sus oídos, si alguien lo conoce!! No para mofa y escarnio, para que se moleste en preguntar o pensar más cómo redactarlo la próxima vez). Textualmente la traducción correcta sería: Porque una vez calculada la matriz escalonada reducida, sólo queda un vector independiente. Para el que no sepa que es esto de la matriz escalonada reducida (o sea que no ha llegado aún a primer curso de cualquier grado en ingeniería, matemáticas, física, etc.), una matriz es escalonada cuando cumple dos cosas: 1.- Si tiene filas nulas, son las últimas. 2.- La primera posición no nula de una fila está al menos una columna a la derecha de la primera posición no nula de la fila anterior. Es más difícil de enunciar que de entender. Los ejemplos nos aclaran a que nos referimos: A = Una matriz es escalonada reducida cuando es escalonada, el primer elemento no nulo de cada fila (se le llama pivote) es un uno, y cada columna que contenga a un pivote tiene esta entrada como única no nula. La matriz C = Las matrices escalonadas son imprescindibles a la hora de estudiar los temas de Álgebra Lineal, porque nos muestran de un rápido vistazo el comportamiento de los vectores, la discusión de las soluciones de un sistema de ecuaciones lineal, el manejo de las aplicaciones lineales, sus subespacios, los cambios de base, …, en fin, mogollón de conceptos, todos los que estudia, como hemos dicho, el Álgebra Lineal. ¿Y cómo se calculan? Pues haciendo operaciones elementales a las filas de una matriz (no voy a ponerme a explicar aquí y ahora el tema, como podréis comprender; dejaríais de leer). En el caso de la matriz que aparece en el episodio de la serie,
Da la impresión que han querido reflejar con lo de “una vez resuelto el primer nivel, sólo queda un vector independiente”, el resultado de que se obtiene al hacer esa matriz escalonada reducida. Pero tal y como lo han dejado, si no sabes matemáticas, no se entiende nada, y sabiendo, te cuesta comprender por qué han puesto eso. Vamos que queda incomprensible en cualquier caso, y no estamos para decir cosas incorrectas en las poquitas matemáticas que aparecen en las películas, que luego se coge mala fama injustamente. Y claro, viendo estas cosas, uno se pregunta, ¿estaré enterándome bien de las películas y series que veo? ¿Se estarán inventando los diálogos de algo más? ¿O de todo? Ante estas dudas razonables, ya saben, a aprender idiomas y disfrutar de la versión original, que en idiomas tampoco andamos demasiado bien en general. Disfruten de la maravillosa señora Maisel. (Gracias Ana García Lema por recomendármela). Esta dirección electrónica esta protegida contra spambots. Es necesario activar Javascript para visualizarla |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |








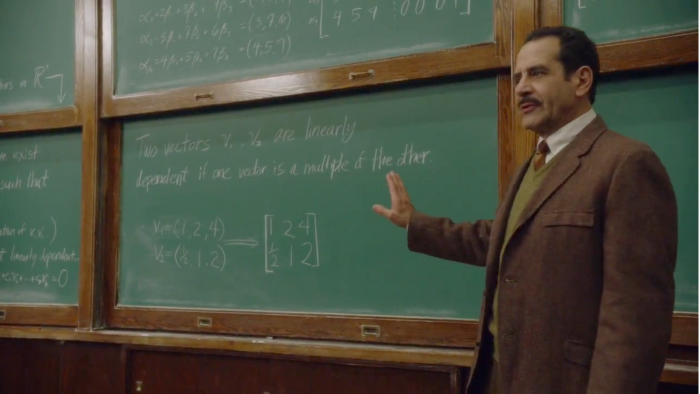
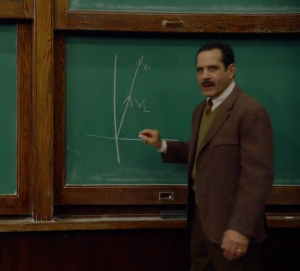
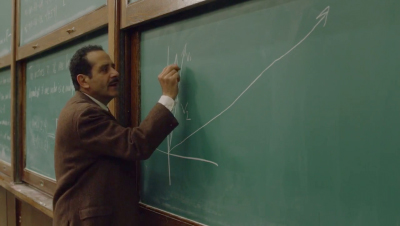 Porque esta aula es un santuario a salvo de las variables del mundo exterior. En esta sala tratamos con valores absolutos y punto. En esta sala esto es lo que cuenta. Estos dos vectores son colineales. (Ver siguiente imagen). Avanzan juntos. Y seguirán avanzando siempre juntos. Este es el voto solemne propio de las matemáticas. En esta sala v2 nunca romperá ese voto para decidir que no necesita al otro vector y fijar por su cuenta una línea independiente. v2 nunca llegará a casa del trabajo y le dirá a v1 “¿Sabes? Creo que necesito mi propio espacio vectorial. Adiós”. (Siguiente imagen: ha dibujado una recta. El supuesto nuevo espacio vectorial al que va a emigrar v2). Porque llegaría el padre de v1 y diría, “¡¡No!! No puedes dejar que v2 haga eso. Tienes que ir a buscar a v2 y que vuelva”. Una solución provisional, porque el padre de v1 no va a poder estar siempre para resolver los problemas de v1. Tomad nota.
Porque esta aula es un santuario a salvo de las variables del mundo exterior. En esta sala tratamos con valores absolutos y punto. En esta sala esto es lo que cuenta. Estos dos vectores son colineales. (Ver siguiente imagen). Avanzan juntos. Y seguirán avanzando siempre juntos. Este es el voto solemne propio de las matemáticas. En esta sala v2 nunca romperá ese voto para decidir que no necesita al otro vector y fijar por su cuenta una línea independiente. v2 nunca llegará a casa del trabajo y le dirá a v1 “¿Sabes? Creo que necesito mi propio espacio vectorial. Adiós”. (Siguiente imagen: ha dibujado una recta. El supuesto nuevo espacio vectorial al que va a emigrar v2). Porque llegaría el padre de v1 y diría, “¡¡No!! No puedes dejar que v2 haga eso. Tienes que ir a buscar a v2 y que vuelva”. Una solución provisional, porque el padre de v1 no va a poder estar siempre para resolver los problemas de v1. Tomad nota. es una matriz escalonada, pero B =
es una matriz escalonada, pero B = 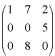 no lo es. Básicamente que los ceros deben ir en forma de “escalera”.
no lo es. Básicamente que los ceros deben ir en forma de “escalera”. es escalonada reducida.
es escalonada reducida.