 143. SOLUCIÓN CONCURSO DEL VERANO DE 2019
143. SOLUCIÓN CONCURSO DEL VERANO DE 2019 |
 |
 |
 |
| Escrito por Alfonso Jesús Población Sáez |
| Viernes 06 de Septiembre de 2019 |
|
Como siempre, atacando por la espalda, cuando empezamos a disfrutar de las vacaciones, aparece septiembre y el nuevo curso. En fin, que todo cada vez pasa más deprisa.
No quiero enrollarme mucho, que la reseña ya es de por si extensa (gracias Nerea por tu comprensión, sobre todo por la dificultad de repasar los símbolos matemáticos con la dificultad añadida de los editores en la red). Simplemente felicitar a todos los participantes e indicar que es el primer año de los quince del concurso que dos de ellos no han dado la película-enigma (uno por confusión con otra con ciertas similitudes, y otro, supongo, porque no ha tenido demasiado tiempo para meterse con ello). Ciertamente intenté que las cuestiones matemáticas fueran más asequibles, y las pistas sobre la película algo más difusas (a lo mejor me pasé, pero es que es, al menos para mí, un título muy conocido). Tenía ganas además de poner algún título de Fritz Lang, uno de mis realizadores favoritos (tengo muchos, pero Lang fue un crack, ya desde la etapa muda). No es su mejor película, obviamente, pero fue la que más me cuadró para esta propuesta “para todos los públicos” (y en este caso me refiero desde el punto de vista de aceptación por la mayor parte de todos; no voy a meter en estas cosas a Bergman o Tarkovski, como cualquiera puede comprender). Cuestiones Matemáticas M – 1.- Si nos dijeran que la suma de un número de cuatro dígitos y sus cuatro dígitos resulta ser 2019. ¿De qué número de cuatro dígitos hablamos? Llamemos n a dicho número. Es obvio que n < 2019. Entonces la cifra de unidad de millar será 1 o 2, y la suma de las tres otras cifras (unidades, decenas y centenas) es como máximo 27 (porque 9 x 3 = 27 en el caso extremo). Por tanto, la suma de los dígitos del número que buscamos es a lo sumo 29, y entonces n ≥ 1990. Llamemos S a la suma de n y los dígitos que lo forman, y sea d un dígito cualquiera.
En principio, hay dos posibles soluciones. Después de resolver la siguiente cuestión, la M – 2, deduciremos cuál de los dos valores es el buscado. M – 2.- La diferencia de años entre el número anterior y el año de estreno de la película tiene el mismo número de divisores que el propio año de estreno de la película. ¿Serán suficientes esos datos para determinar dicho año de estreno? Dar un razonamiento a favor o en contra. Adelantándonos un poco, y utilizando información que posteriormente averiguaremos, como el año de estreno de la película es 1955 = 5 • 17 • 23, el número de divisores es 8 de acuerdo con una conocida expresión (si n = p1d1 • p2d2 • …. • prdr, entonces el número de divisores de n es el producto div(n) = (d1 + 1) (d2 + 1) …. (dr + 1) De las dos posibles soluciones del apartado anterior M – 1, como 1995 – 1955 = 40 = 23•5 (que tiene 8 divisores también ya que son (3+1) (1+1), de acuerdo con la fórmula anterior), pero 2013 – 1955 = 58 = 2 • 29, tiene sólo (1+1) (1+1) = 4 divisores. Por tanto, la solución de M – 1 es 1995. Sin ningún otro dato adicional, no es posible determinar el año x de estreno si no lo supiéramos, ya que, según el enunciado, lo que debe cumplirse es que div(1995 – x) = div(x), y eso lo cumplen un montón de valores de x: 1955, 1957, 1961, 1965, 1969, 1971, 1975, 1981, 1985, 1993. En definitiva, que harían falta más datos para determinar el año. M – 3.- La acción tiene lugar en el siglo de las luces, en un año tal que al ser dividido por 2 y por 4 da resto 1, y al hacerlo por 3 y por 5 da resto 2. ¿A qué año nos referimos? El siglo de las luces es el siglo XVIII, de modo que buscamos un valor entre 1701 y 1800. Al tener los restos y los divisores, parece un claro ejemplo de utilización del conocido como teorema chino de los restos. Veamos si ese resultado nos lleva a la solución. Si n es el número que buscamos, los datos que nos dan son n ≡ 1 mod 2 n ≡ 1 mod 4 n ≡ 2 mod 3 n ≡ 2 mod 5 La primera condición nos indica que n = 2k + 1, para algún valor de k. Sustituyendo ese valor en la tercera condición, tenemos que 2k + 1 ≡ 2 mod 3 Simplificando llegamos a que 2k ≡ 1 mod 3. Para despejar k, basta con multiplicar la congruencia por un valor que nos dé coeficiente uno para k módulo 3. Eso se logra al multiplicar por 5, ya que 10 ≡ 1 mod 3. Eso nos lleva a que k ≡ 5 mod 3, y por tanto k es de la forma k =3t + 5, para algún valor de t. Sustituyendo k en la igualdad que teníamos de n, llegamos a que n = 2(3t + 5) + 1 = 6t + 11 Del mismo modo que en el paso anterior, sustituimos en la cuarta condición, teniendo que 6t + 11 ≡ 2 mod 5, es decir, 6t ≡ 1 mod 5. Multiplicando la ecuación por 6, se concluye que t ≡ 6 mod 5, es decir, que t = 5r + 6, para algún valor de r. Sustituyendo ese valor en la última expresión que habíamos deducido para n, se tiene que n = 6 (5r + 6) + 11 = 30 r + 47 Finalmente, empleando el segundo dato (que me lo he saltado por simple despiste), tendremos que 30 r + 47 ≡ 1 mod 4, o lo que es igual, 30 r ≡ - 46 mod 4, o análogamente, 2r ≡ 2 mod 4, o r ≡ 1 mod 4. De ahí, n = 30(4s + 1) + 47 = 120 s + 77 Para s = 14 encontramos el único valor entre 1701 y 1800, que resulta ser 1757. M – 4.- En un cierto día, la luna se ve con la sombra pasando a través de puntos diametralmente opuestos. Si el centro del arco circular que se está formando se encuentra en la circunferencia de la luna, determinar la proporción exacta de la luna que no está en la sombra. ¿Cuál es dicha proporción (en modo exacto)? Llamemos r al radio de la luna y C su centro. Sea R el radio del arco circular que forma la sombra y O el centro de dicho arco. Sean P y Q los puntos donde la sombra corta a la circunferencia de la luna. Sea x el área del triángulo POQ, y el área de la región entre PQ y el arco que pasa por P y Q centrado en O, y z el área de la región limitada entre los dos arcos (o sea el área de la sombra). Como PC = CQ = r, OP = OQ = R, y el ángulo POQ es de 90 grados (dado que PQ es un diámetro), entonces x + y = ¼ π R2 = ¼ π ( También se observa que la suma de las superficies y y z es la mitad del área del círculo centrado en C, es decir, y + z = ½ π r2 Entonces x + y = y + z, y de ahí se sigue que x = z. Como x es igual al área del triángulo rectángulo POQ, entonces z = x = ½ (√2 r)2 = r2. El área de la región que no está en la sombra es igual al área del círculo completo centrado en C menos z: π r2 - r2 = r2 (π - 1) Por tanto, la proporción exacta de la Luna que no está en sombra es
Si se desea en porcentaje, esa fracción es aproximadamente 0.6817…, es decir, un 68.17%. M – 5.- Los carruajes tardaban exactamente tres horas en ir y volver a la ciudad más próxima situada 30 millas al oeste. Llegando octubre, el recorrido se dilataba media hora más. Estimar en ese caso la velocidad del viento. A falta de más datos (tiempo de descanso en el destino, etc.), supondremos que el carruaje circula a velocidad uniforme. Entonces ésta será Vcarruaje = espacio/tiempo = 60/3 = 20 millas por hora. Llamemos w a la velocidad del viento. En uno de los dos trayectos (ida o vuelta), el carruaje circula a favor del viento, de manera que su velocidad será de 20 + w, mientras que en trayecto opuesto será de 20 – w. Entonces el tiempo que tarda en cada trayecto será en un caso
Resolviendo la ecuación tenemos que la velocidad del viento será w = M – 6.- Si la forma de la suela del zapato (excluyendo el talón, que está más reforzado) sigue la ecuación 4x2 + y2 ≤ 4, con y ≥ 0, y el desgaste del material que conforma la suela se expresa en cada punto (x, y) por la función f(x, y) = 4x2 + y2 + 4x – 3y, determinar en qué punto exactamente se ha hecho el agujero, justificando el resultado. Si el desgaste de material viene dado por f(x, y), parece lógico pensar que el agujero se hará donde mayor desgaste de la suela se produzca (suela que viene dada por la semielipse positiva centrada en (0, 0) y de semiejes 1 y 2, respectivamente, ya que 4x2 + y2 ≤ 4, con y ≥ 0, es lo mismo que
x2 + Por tanto, buscamos el máximo absoluto de la función desgaste, condicionado a la suela del zapato. Dicho máximo se alcanza con seguridad ya que la función de dos variables que describe el desgaste es continua (es polinómica) y la suela del zapato (la semielipse) es un conjunto cerrado (contiene el borde, es decir, los puntos frontera) y acotado (se puede incluir en un entorno de centro (0, 0) y radio 2.1, por ejemplo). En virtud del teorema de Weierstrass, la función desgaste alcanza con seguridad el máximo y el mínimo absolutos dentro de la semielipse. Utilizaremos para localizar el máximo absoluto el método de los multiplicadores de Lagrange. Definimos entonces la función auxiliar de Lagrange F(x, y) = 4x2 + y2 + 4x – 3y + λ(4x2 + y2 – 4) En primer lugar, veamos si los extremos relativos de f(x, y), son posibles candidatos a extremos absolutos. Como las derivadas parciales de f son, respectivamente, 8x + 4 y 2y – 3, el único extremo posible en R2 será (–1/2, 3/2). Como dicho punto se encuentra dentro de la suela del zapato (es decir, está en S, siendo S = {(x, y) / 4x2 + y2 ≤ 4}), es un posible candidato a extremo absoluto. Como seguramente el lector recuerde, para poder aplicar el método de los multiplicadores de Lagrange, los puntos obtenidos deben ser regulares de S. Y desgraciadamente, pueden alcanzarse extremos en puntos no regulares (a los que no podemos, insisto, aplicar el método de los multiplicadores de Lagrange). Así que, procedamos a localizar los puntos no regulares de S. Éstos son aquellos para los que el gradiente de la función g(x, y) = 4x2 + y2 – 4 no es máximo, es decir, el rango(∇g) < 1. Como ∇g(x, y) = (8x, 2y), el rango es nulo, si, y sólo si (x, y) = (0, 0). Y (0, 0)∈S, de modo que también es candidato a extremo. Aplicando la condición necesaria de extremo a F, obtenemos el sistema
Con un poco de paciencia (despejando y sustituyendo) obtenemos como solución los puntos
Ambos están en S, de modo que dos nuevos candidatos. Finalmente debemos considerar los puntos de la frontera y = 0 (los del borde de la elipse, son los anteriores). Estos son (1, 0), (–1, 0), y además aparece el (–1/2, 0), ya que al hacer y = 0, la función desgaste queda h(x) = 4x2 + 4x, y su derivada se anula en –1/2. Al verificarse el teorema de Weierstrass, basta con que evaluemos la función desgaste en todos esos candidatos a extremo. El valor mayor corresponderá al máximo absoluto, y el menor al mínimo absoluto. El primero es en el punto (1, 0) y el segundo en (–1/2, 3/2). Hubiera quedado más acorde con la película que saliera en el medio de la suela, pero el caso es que el máximo absoluto que resulta con estos datos es 8, que se alcanza en el punto (1, 0). M – 7.- Si imagináramos que el protagonista se encuentra en el punto A(0, 0) de un también imaginado plano coordenado, al reiniciar su camino se desplaza 1 unidad a la derecha, después r al norte, r2 a la izquierda, luego r3 al sur, r4 al este, r5 al norte, continuando con ese mismo patrón. Si lo hiciera indefinidamente, y siendo r un número positivo menor que 1, llegaría a un punto B(x, y). Demostrar que AB > 7/10. Denotemos por Pn = (xn, yn) el punto en el que se encuentra después de n movimientos. Así, tenemos que P0 = A = (0, 0), P1 = (1, 0), P2 = (1, r), P3 = (1 – r2, r), …. Es fácil comprobar que, para cada m ≥ 2, x2m-1 = x2m = 1 – r2 + r4 – …. + (–1)m–1 r2m–2 y2m = y2m+1 = r – r3 + r5 – …. + (–1)m–1 r2m–1 Utilizando la suma de los términos de una progresión geométrica, concluimos que
Así, AB2 = x2 + y2 =
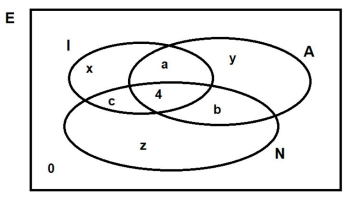
M – 8.- ¿Cuántos?
Tomando prestado el diagrama de uno de los concursantes, lo que buscamos en realidad es el valor de a + b + c. Tenemos los siguientes datos: Card(I) = 74, Card(A) = 17, Card(N) = 25, Card(I∩A∩N) = 4. Aplicando el principio de inclusión-exclusión, Card(I∪A∪N) = Card(I) + Card(A) + Card(N) – Card(I∩A) – Card(I∩N) – Card(A∩N) + Card(I∩A∩N). Entonces, despejando, se tiene que Card(I∩A) + Card(I∩N) + Card(A∩N) = Card(I) + Card(A) + Card(N) + Card(I∩A∩N) – Card(I∪A∪N) = 74 + 17 + 25 + 4 – 100 = 20. De acuerdo con el diagrama, (4 + a) + (4 + b) + (4 + c) = 20, luego a + b + c = 20 – 12 = 8. M – 9.- Calcular razonadamente el volumen de uno de estos objetos de altura h, sabiendo que se refuerza como vemos en la imagen con seis aros de hierro circulares, tres de ellos de diámetros distintos d1, d2 y d3 (d1 < d2 < d3). hasta la mitad; los otros tres repiten esos valores simétricamente, tal y como se observa en la imagen.
El problema de modelización que pongo todos los años en el que el concursante debe “buscarse un poco la vida” aportando los datos que considere pertinentes para encontrar una solución práctica. Prácticamente todos los participantes han utilizado el cálculo integral para determinar el volumen de revolución de una parábola en la que previamente han colocado los valores d1, d2 y d3 que se indicaban. No incluyo las operaciones concretas por no alargar este texto. A todos les he dado la puntuación completa (salvo a los que simplemente dan un valor sin indicar como se obtenía, obviamente). M – 10.- ¿Qué barril se quedó sin comprar? El cliente pagó la misma cantidad (14 libras) por los de mejor calidad y por los de peor, y sabiendo que los primeros valen el doble que los segundos, eso significa que la suma de galones de los de mejor calidad es justamente la mitad que los de inferior. Se trata por tanto de agrupar los galones en dos grupos, uno con el doble de galones que el otro, dejando uno de ellos sin contabilizar. Si uno de esos grupos suma el doble del otro, eso significa que al menos uno de ellos debe sumar una cantidad par de galones. La suma de todos los barriles es 98 galones. Vayamos probando: 1.- Dejamos fuera el barril de 3 galones. El resto suma 95 galones. Hay que dividir 95 en tres partes, ya que una debe ser el doble de la otra. Eso no nos da números enteros, luego no es solución. 2.- Apartamos el barril de 13 galones. El resto suma 85 galones. Tampoco es divisible por 3. 3.- Quitamos el barril de 15 galones. El resto suma 83 galones. Tampoco es posible. 4.- Si eliminamos el de 17 galones, el resto pesa 81 galones. En un grupo por tanto debemos tener 27 galones y en el otro 54. Pero si intentamos sumar 27 galones con los datos de los barriles que tenemos, comprobamos que no es posible. 5.- Descartando el de 19 galones, nos quedarían 79 galones, que no es múltiplo de tres. 6.- Finalmente, apartando el de 31 galones, tendríamos 67 galones, que tampoco es divisible por tres. Por tanto, con esos datos no hay solución. ¿Y cómo puede ser? Pues porque el “listo” que esto escribe, con las prisas, cambió un barril: el de 3 galones, debería haber sido de 8 galones, y entonces, el cliente hubiera comprado los barriles de mejor vino de 13 y 15 galones a 0.50 libras el galón, y los de 8, 17 y 31 galones a 0.25 libras el galón, quedando por tanto sin vender el barril de 19 galones del que no sabríamos si era de vino de mayor o menor calidad. Mil disculpas. Ha habido participantes que lo han razonado perfectamente; al resto se les ha dado una puntuación proporcional al buen planteamiento que hayan realizado. M – 11.- A la entrada de la fiesta, una campana anunciaba con un toque la llegada de los invitados. Cuando llegó el primero, la campana sonó por primera vez. Cada vez que la campana sonó después, el número de invitados que llegaba eran dos más que los que habían llegado la vez que la campana sonó anteriormente. Si la campana tañó n veces, ¿cuántos invitados estuvieron en la fiesta?
La cuestión es muy sencilla, a partir de una tabla como la siguiente: Veces que toca la campana 1 2 3 4 … n Invitados que llegan 1 3 5 7 … 2n - 1 Por tanto, la suma total de invitados es la suma de la segunda fila, es decir, 1 + 3 + 5 + 7 + …. + 2n - 1 Utilizando la suma de los primeros sumandos de una progresión aritmética, se tiene que
M – 12.- Para juzgarlo, calcúlese la probabilidad de obtener en una mano de 7 cartas (las cinco del reparto inicial más 2 de cambio) cuatro reyes. Comparar con la probabilidad de obtener en las mismas condiciones únicamente tres reyes. Calcular ambas probabilidades es realmente sencillo. Utilizaremos como referencia la baraja francesa de 52 cartas (la que suelen utilizar las películas anglosajonas). Como ir sacando cuatro reyes de la baraja (sin reemplazar las cartas) responde a sucesos independientes, basta con multiplicar las sucesivas probabilidades de extraer un as, luego un segundo as, etc.; una vez obtenidos los cuatro, las restantes nos resultan indiferentes. Ahora bien, los ases pueden salir en cualquier momento de las siete extracciones (es decir, puede ser KKKKXXX, o XKXXKKK), de modo que hay que multiplicar la probabilidad por el número de sucesos posibles. Éstos serán
Por tanto, p(4 reyes) = 35 En el caso de tres reyes, la probabilidad se calcula exactamente igual, con la diferencia de que, sacados tres reyes, después necesitamos que salga cualquier carta restante de la baraja, excepto el cuarto rey. Por tanto, p(3 reyes) = 35 es decir, es mucho más probable, del orden de prácticamente 6 de cada 1000 partidas jugadas, mientras que la de los cuatro reyes, del orden de 1 de cada 10000 partidas. De modo que es bastante acertado concluir que hubo trampas, más aún teniendo en cuenta que su oponente había obtenido ¡¡cuatro reinas!! M – 13.- ¿Qué relación tiene
M – 14.- El emblema divide al círculo en tres regiones. ¿Son iguales? ¿Podrían serlo?
Respecto a la cuestión M – 13 , al tener una raíz cuadrada de dos en liza, lo primero que a uno le viene a la cabeza es involucrar una distancia, o si sus matemáticas son más elementales, la hipotenusa de un triángulo rectángulo (que es una distancia). Tampoco es muy complicado darse cuenta que el punto B, al ser el punto de intersección de la bisectriz del primer cuadrante (o sea, la recta y = x) y la circunferencia unidad (x2 + y2 = 1) tiene por coordenadas (
Algún concursante (más sofisticado y perspicaz que yo), ha recordado que la cantidad dada es la razón o proporción de plata, y ha buscado el rectángulo de plata (aquel cuya proporción entre base y altura es ese valor) que contiene parte del emblema (no es muy complicado, basta darse cuenta del valor de la diagonal BC, por ejemplo). Lo destacable es que lo ha relacionado con el argumento de la película, ya que en ella se dice que las monedas que guardaba el pirata Barbarroja eran precisamente de plata y el medallón del esqueleto de Barbarroja también se dice que es de plata. Excelente observación, que debo reconocer como proponente, en la que nunca pensé, pero que ahí está. Por si fuera poco, otro concursante ha encontrado un curioso juego de palabras. El emblema de los Mohume es una Y (que en inglés se pronuncia “guay”, escribiéndola tal cual), y Why not es el nombre de la taberna del pueblo en la novela (Why también se pronuncia “guay”). M – 15.- El documento está doblado varias veces formando un cuadrilátero ABCD convexo e inscrito en el medallón (es decir sus cuatro vértices tocan la circunferencia que determina el medallón, como aparece en la imagen). Las diagonales AC y BD se cortan en el punto E. Sabiendo que AB = 39, AE = 45, AD = 60 y BC = 56, determinar la longitud de CD.
Empecemos por la semejanza de triángulos: los triángulos AEB y DEC son semejantes (tienen un vértice común y los ángulos en E son opuestos por un vértice). Por tanto,
Por la misma razón, son semejantes AED y BEC, por lo que
De la primera y la tercera de estas fracciones, tenemos que Por otra parte, el teorema de Ptolomeo afirma que AD • CB + AB • CD = BD • AC Sustituyendo los valores conocidos, tenemos que 60 • 56 + 39 • CD = (42 + ED) • (45 + EC) (3) De (1), se tiene que CD = 60 • 56 + 39 • Resolviendo la ecuación, se llega a que ED = 21 (la solución ED = - 75 obviamente la rechazamos), y de ahí, como CD =
Cuestiones culturales y cinematográficas
C – 1.- Es curioso que una película, en apariencia de aventuras, no se estrenara en España hasta pasados 27 años de su estreno internacional, y que además se hiciera por televisión, concretamente el domingo 6 de junio de 1982, por la segunda cadena de televisión española, a las 22:15, aunque se había programado para el sábado 6 de febrero de ese mismo año por la primera cadena, pero “sin ninguna explicación”, el ente público la cambió. En salas comerciales se pudo ver, como nos comentan los concursantes, en circuitos restringidos como salas de arte y ensayo, cine clubs o filmotecas. Así, en Madrid, el cine Bellas Artes la programó el 28 de agosto de 1987, en Sevilla el multicine Cristina la programó el 28 de mayo de 1988, y también el cine club Arquitectura el 15 de marzo de 1990. En Bilbao el 15 de noviembre de 2005 en el cine club FAS, uno de los más antiguos de España en activo, por cierto (seguramente el que más, pero habría que confirmarlo). También nos indican que en Vigo o Gijón se pasó por salas, pero sin prueba que lo demuestre, lo dejamos en el aire. En Valladolid, las salas Casablanca (aún en activo, especializadas en cine de autor) la programó el 7 de abril de 1988 (adjunto el anuncio de esa fecha del periódico El Norte de Castilla); posteriormente el viernes 11 de septiembre de 1988 la filmoteca de la Caja de Ahorros Popular también la pasa en un ciclo dedicado al realizador alemán. Curiosamente, el viernes 30 de agosto (a un día de finalizar el plazo de envío de las respuestas de este concurso) la Filmoteca Española la puso a las 18:00 en el Cine Doré, aunque allí la han programado más veces.
C – 2.- Aunque los concursantes han hecho referencia al desplante del director alemán a Goebbles y su huida a Norteamérica, además de su ascendencia judía por parte de madre, y que en España el gobierno de Franco le tendría alguna animadversión, eso implicaría que ninguna película suya se hubiera estrenado por aquí, y eso no fue así. En este caso, nada que ver con la política. Ni a la productora (la Metro-Goldwyn-Mayer), ni al director, les gustó demasiado el producto final, por lo que no tenían demasiado interés en estrenarla en los EE. UU. Esto fue fruto de que al realizador se le impuso un guion, un formato en el que no estaba cómodo (el CinemaScope) y allá donde pudo fue modificando cosas durante el rodaje. Por ello, ni unos ni otros quedaron contentos. Finalmente se estrenó el 12 de mayo de 1955 en sesiones dobles y de cine infantil, sin ningún tipo de promoción, casi avergonzándose de proyectarla. Tampoco hicieron lo mínimo por distribuirla a otros países. En un viaje por Italia, el crítico y cineasta francés Luc Moullet la vio, y escribió una pequeña crítica en la prestigiosa Cahiers du Cinema (en el nº 62, para más detalles) calificándola de genial. Muy cerca de la redacción de la revista se encontraba el cine Mac-Mahon (en la homónima avenida), que se había especializado en estrenar películas que no hubieran llegado a Francia por circuito comercial, en versión original. Y en 1960 logran estrenarla publicitando el hecho como un gran triunfo. ¿Y cómo es posible que no gustara a los yanquis, siendo, porque lo es, una gran película? Hay que verla para descubrirlo, pero se trata de una película (y una novela) incómoda para lo que podríamos llamar, las mentalidades “políticamente correctas”. Nos han hecho a la idea de que a los niños se les debe mostrar un mundo bonito, perfecto, que ya tendrán tiempo de descubrir la realidad cuando crezcan. Hombre, no vamos a poner a los niños ante hechos salvajes o truculentos, eso está claro, pero tampoco podemos estirar el mito de los Reyes Magos al máximo, porque al final la decepción es tan mala como lo que pretendíamos reservar. Es una obra (novela y película) oscura, incómoda, sobre todo para los adultos, y eso, en 1955 costaba. Aunque de 1953 se estrenó Raíces Profundas (Shane, George Stevens, EE. UU.), con la que tiene no pocas similitudes, y sin embargo hasta la “oscarizaron”. Pero claro, no era lo mismo un western (para los que la mayoría no veía más allá de tiros y caballos) con un personaje íntegro hasta la médula, que la lejana costa inglesa con un protagonista vividor cínico, ambicioso y sin escrúpulos. C – 3.- El título original, Moonfleet, lugar inexistente en la realidad, es un compuesto de Moon (Luna) y Fleet (admite varios significados: el más evidente, Flota, pero también hace referencia a un estuario, una ría, una zona de marismas; y como verbo, ondear, ondular, rielar. Todas las acepciones cuadran, tal y como se indica en el párrafo que va a continuación de la novela), aunque el autor indica en la novela que “cuando era un niño pensaba que este lugar se llamaba Moonfleet porque en una noche tranquila, ya sea en verano o durante las heladas invernales, la luna brillaba muy intensamente en la laguna; pero luego aprendí que era la abreviatura de la "flota Mohune", de los Mohunes, una gran familia que una vez fueron los señores de todas estas partes”. C – 4.- Todos los concursantes han descrito que se asusta de una mano que sale de debajo de la tierra, de uñas muy largas, sucia y movimiento lento, tratando de asustar al niño. De un contrabandista en el contexto de la película, obviamente. Sin embargo, a lo que me refería con la cuestión era a quien concretamente pertenece la mano (). Fritz Lang tenía a gala, a modo de marca de fábrica, filmar su propia mano en sus películas. Esta es su mano (maquillada para la ocasión, claro; pensé que bastaba esa insinuación, para que los lectores lo dijeran, pero ya he visto que no). Así que sólo 5 puntos para todos en esta ocasión, excepto para uno que le doy 6 al darse cuenta de que la mano aparece exactamente en el “pinuto” 3:14, ja, ja, ja. C – 5.- Los diez puntos los alcanzan los que hayan indicado que los barriles de contrabando al subir la marea chocaban entre si flotando en la cripta que servía de escondite que se encontraba justamente bajo la iglesia (con esa intención se hizo la pregunta). El sonido se amplificaba a través de las cavidades, percibiéndose en la iglesia con cierto estruendo, que los lugareños atribuían al fantasma de Barbarroja (y obviamente difundido y amplificado por los propios contrabandistas, interesados en que se aceptara la explicación sobrenatural; vamos como algunos otros que hay por ahí que pretenden que creamos en …, bueno mejor me callo y que cada cual concluya). No obstante, los barriles son omnipresentes en toda la trama: el chiquillo se cae de un barrilete y gracias a eso descubre el medallón en el ataúd de Barbarroja, se utiliza medio barril para acceder al pozo donde se halla el diamante, en los barriles se guarda la preciada mercancía de contrabando. Los que hayan indicado alguna de éstas razones, más obvias, tienen cinco puntos. C – 6.- El papel encontrado dentro del medallón de Barbarroja describe varias citas bíblicas que el sacristán/sepulturero Felix Ratsey (buen conocedor de la Biblia) descubre (en la película) al instante que están mal citadas (el versículo no corresponde al texto). Este dato hace pensar a Jeremy Fox que el número incorrecto que sustituye al verdadero debe indicar algo. Tomando de cada cita la palabra que corresponde al número incorrecto (la secuencia es 10 - 6 - 15 -11 – 10) se compone la frase Treasure fourscore feet deep well, cuya traducción sería algo así como Tesoro a 80 pies de profundidad del pozo (obsérvese que fourscore son cuatro veintenas, es decir, ochenta). Eso les lleva al pozo de Hollisbrooke, que se dice el más profundo de Inglaterra, localidad en la que además Barbarroja fue gobernador del castillo. No entiendo por qué los guionistas cambiaron el nombre del lugar original, Carisbrooke, por el imaginario de Hollisbrooke. En este lugar hay un castillo medieval visitable y de cierto interés histórico y turístico, y con una Casa del pozo (Well-House) que data de 1587 y con una curiosa estructura de rueda de tracción animal y eólica para sacar agua. Es una de las mayores atracciones del castillo, donde se forman grandes colas de gente para observar a los burros de Carisbrooke trabajar (recordemos que así se mueve también en la película). C – 7.- Se trata de un símbolo heráldico denominado pall, y es el emblema de la familia Mohune. Uno de los concursantes ha tenido la paciencia de indicar el minuto exacto donde aparece el citado símbolo:
C – 8.- La caratula del DVD editado en España, el menú de opciones, etc., tienen el título con el que se conoce, Los contrabandistas de Moonfleet, heredada de la versión estrenada en Francia, pero cuando lo reproducimos en la versión doblada al castellano, la voz en off dice Los aventureros de la noche, que es cómo se emitió por televisión española y se anunció en los medios de comunicación. Siendo el año 1982, ya instaurada la democracia y la correspondiente eliminación de la censura desde hacía unos años, no entiendo ese otro título, y no he encontrado por qué en ninguna parte. Sólo cabe la especulación de que quizá no se quería presentar en una película, aparentemente de aventuras, y por tanto para todos los públicos, una actividad ilícita en el título como es el contrabando. Pero insisto, es pura especulación. C – 9.- La película y la novela tienen muchas diferencias (como decía un participante, casi es más breve indicar las coincidencias). Hago una lista de todas las que nos habéis mandado, aunque como sólo se pedían seis, ese número basta para alcanzar los diez puntos de la pregunta, aunque algunos os habéis explayado: 1.- El Barbarroja de la película es en la novela Barbanegra. 2.- En la novela la posada se llama Why Not, mientras que en la película es The Halberd. 3.- En el libro, es el corpulento Elzevir Block (mesonero encubierto de la taberna) quien se encarga de John Trenchard (llamado John Mohune en el film), mientras que en la película es el galante contrabandista Jeremy Fox (administrador de los bienes de la familia Mohune). 4.- Además, Elzevir Block es el héroe de la novela, pero en el film es un contrabandista sin importancia y uno de los villanos (de hecho, es el que se enfrenta con una enorme lanza a Jeremy Fox en el duelo en la posada). 5.- En la novela, el joven Trenchard es, desde el primer momento, un habitante del pueblo de Moonfleet, y no un recién llegado como ocurre en la película. 6.- John es huérfano, pero en la novela vive con su tía Jane. Este personaje desaparece en la versión cinematográfica, donde solo se menciona la muerte de su madre Olivia. 7.- En la película, John es mucho más aniñado (tiene 11 o 12 años) y temeroso que en la novela (en la que tiene 15 años), y es más adulto y audaz. 8.- En el libro, tras encontrar John el diamante y subir del pozo, Elzevir lucha con el hombre que limpia las instalaciones, quien acaba cayendo al pozo. En la película, se queda inconsciente en el borde del pozo. 9.- En la novela, John se hace con la clave del acertijo gracias a una pista facilitada involuntariamente por la tía, pudiendo localizar así el escondrijo (el castillo donde estuvo retenido el rey Carlos I). 10.- En el libro, John viaja con la biblia de su madre y usa esta para descifrar el mensaje, pero lo hace dentro de la cueva donde se refugian. En la película lo descifran sin la biblia y escondidos en el camino tras unos arbustos. 11.- En la novela, John y Elzevir renuncian al diamante pues un malintencionado joyero holandés les dice que no es auténtico, sino de cristal. Esto no ocurre en la película. 12.- En la novela, Elzevir acoge al muchacho desde el principio, pero en la película, Jeremy tratará por todos los medios de deshacerse del muchacho y la compenetración será progresiva. 13.- John y Elzevir van varios años a la cárcel y después son enviados a Java, pero durante el trayecto, la embarcación naufraga frente a la costa de Moonfleet. Aunque John logra llegar a tierra, Elzevir muere ahogado. En la película no van a la cárcel y Jeremy Fox muere malherido por Ashwood, adentrándose en la mar en un bote. 14.- En el film, el magistrado Maskew no es el padre (como ocurre en la novela), sino el tío de Grace (la niña de quien está enamorado John en la novela). 15.- A diferencia de lo que sucede en el libro, en el film el párroco no interviene en las actividades delictivas de su comunidad, al menos de una forma cómplice. 16.- En la novela, John acaba casándose con Grace y tienen 3 hijos. La película termina con ellos niños. 17.- En la novela a Maskew lo matan accidentalmente sus propios hombres mientras persiguen a los contrabandistas, mientras que en la película Jeremy Fox lo despeña . 18.- La acción en la novela trascurre a lo largo de varios años y en la película sólo en unos pocos días. 19.- En el libro se disfrazan de carreteros, de albañiles y de marineros mientras que en la película Jeremy Fox se disfraza de soldado. 20.- En el libro el que resulta herido es John, en una pierna, mientras que en la película hieren a Jeremy Fox en una mano. 21.- En la película el castillo donde está el diamante se llama Hollysbrooke, en el libro se llama Carisbrooke. C – 10.- El diamante de Moonfleet de John Meade Falkner (el título original es Moonfleet), fue la novela elegida para iniciar este proyecto, disponible desde el 21 de mayo. Los libros de la colección presentan prólogos inéditos de Arturo Pérez-Reverte, portadas diseñadas en exclusiva por el célebre ilustrador Augusto Ferrer-Dalmau, y la traducción está hecha en exclusiva por la escritora Dolores Payás. Una magnífica iniciativa a la que deseamos larga vida. C – 11.- Varios cineastas franceses (ya comentamos antes el aprecio de los críticos de Cahiers por ella) han manifestado su interés y reconocimiento por Fritz Lang. El más conocido que manifestó su devoción por esta película fue François Truffaut, aunque tampoco escatimaron elogios Serge Daney, Jean Luc Godard, Luc Moullet o Bernard Eisenschitz. Cualquiera de estos nombres sirve como respuesta. C – 12.- Hergé (seudónimo de Georges Prosper Remi), autor de la célebre serie de historietas gráficas de Tintín, reconoció que Tintín y el capitán Haddock fueron inspirados en sus características básicas por John Trenchard y Elzevir Block, respectivamente, de la novela. C – 13.- Película: Los contrabandistas de Moonfleet (Moonfleet, Fritz Lang, EE. UU., 1955) Novela: Moonfleet (1898) de John Meade Falkner.
Puntuaciones Es realmente gratificante comprobar el magnífico nivel de todos los participantes (quiero hacer una mención especial a Alba Diez Mariño, que siendo una chica de 14 años solamente, ha resuelto, con las herramientas matemáticas que conoce a esa edad, la mayor parte de las cuestiones; algunas, era imposible que las hiciera, pero ha sido además honesta y no ha pedido a nadie que se las resolviera). Salvo malentendido de algún enunciado, todos han afrontado perfectamente todas las cuestiones matemáticas. Respecto a las de cine, siempre baja un poquillo, pero internet suele suplir las lagunas. 1.- Alejandro Apezteguía.- 274 puntos 2.- Francisco Pi Martínez.- 265 puntos 3.- Marta Pérez Ceballos.- 262 puntos 4.- Pedro Pablo Palacio.- 229 puntos 5.- Alba Diez Mariño.- 196 puntos 6.- Celso de Frutos de Nicolás.- 118 puntos 7.- Alberto Gustavo Colomo.- 10 puntos Agradezco a todos su buenísima disposición, la aceptación de la propuesta, y sus elogios (inmerecidos). Espero que hayan pasado de verdad un buen rato. En breve recibiréis un mail, algunos para pediros una dirección postal a la que enviaros un pequeño obsequio de DivulgaMAT, y los demás para comentaros un poco las puntuaciones de cada cuestión, una vez hayáis leído las soluciones. Esta dirección electrónica esta protegida contra spambots. Es necesario activar Javascript para visualizarla |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |







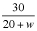 , y en el otro
, y en el otro 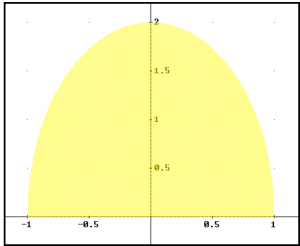
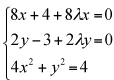
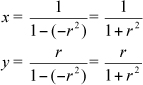
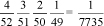 ≈ 0.0001292824822….
≈ 0.0001292824822….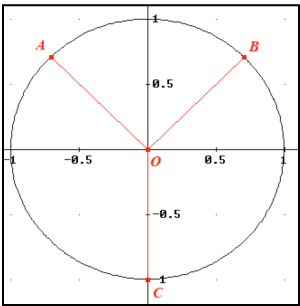 Atacamos en conjunto ambas cuestiones. Claramente el anillo circular de la película tiene marcada una Y, como indica la figura (es decir, si colocamos como centro O el punto desde el que parten los tres segmentos de la Y, los superiores están sobre las bisectrices del primer y segundo cuadrante, respectivamente). La primera parte de la cuestión
Atacamos en conjunto ambas cuestiones. Claramente el anillo circular de la película tiene marcada una Y, como indica la figura (es decir, si colocamos como centro O el punto desde el que parten los tres segmentos de la Y, los superiores están sobre las bisectrices del primer y segundo cuadrante, respectivamente). La primera parte de la cuestión 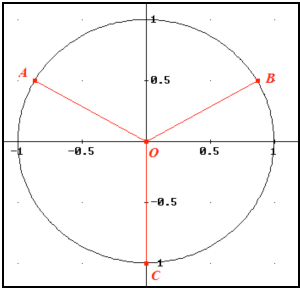 Entonces para que fueran iguales, deberíamos considerar ángulos (los tres) de 120º. Entonces la figura sería como la de la segunda imagen, que claramente no es la del anillo de la película. He tomado la circunferencia de radio unidad, de modo que el área del círculo sería 2π, y por tanto, cada parte sería de superficie 2π/3. Como ven no hace falta hacer ninguna integral, pero si la hacen, háganla en coordenadas polares que es mucho más rápida y sencilla su resolución.
Entonces para que fueran iguales, deberíamos considerar ángulos (los tres) de 120º. Entonces la figura sería como la de la segunda imagen, que claramente no es la del anillo de la película. He tomado la circunferencia de radio unidad, de modo que el área del círculo sería 2π, y por tanto, cada parte sería de superficie 2π/3. Como ven no hace falta hacer ninguna integral, pero si la hacen, háganla en coordenadas polares que es mucho más rápida y sencilla su resolución.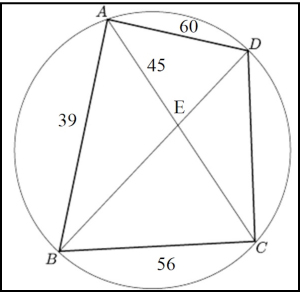 NOTA: En efecto, las medidas de la imagen no están a escala (otro lapsus). No obstante, podemos hacer perfectamente el ejercicio.
NOTA: En efecto, las medidas de la imagen no están a escala (otro lapsus). No obstante, podemos hacer perfectamente el ejercicio.
 Desde hace tres años existe una publicación digital llamada
Desde hace tres años existe una publicación digital llamada 