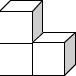
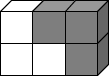
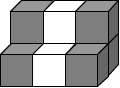
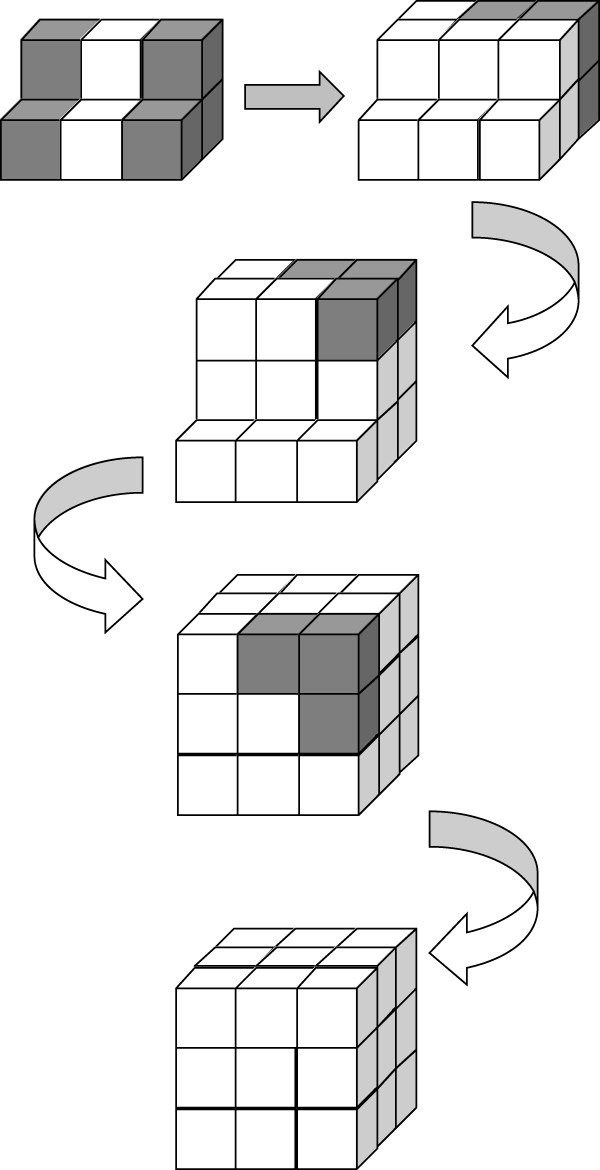
11. (Julio 2020) SOMA: antepasados y descendientes
11. (Julio 2020) SOMA: antepasados y descendientes |
 |
 |
 |
| Escrito por Vicente Meavilla Seguí |
| Miércoles 15 de Julio de 2020 |
|
Las disecciones del cubo proporcionan una rica fuente de inspiración a los diseñadores de rompecabezas tridimensionales. En este artículo ofrecemos una selección de puzles 3D obtenidos a partir del poliedro regular que, en la cosmología platónica, representaba la tierra. 1. El cubo diabólico
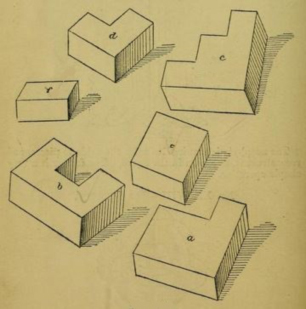
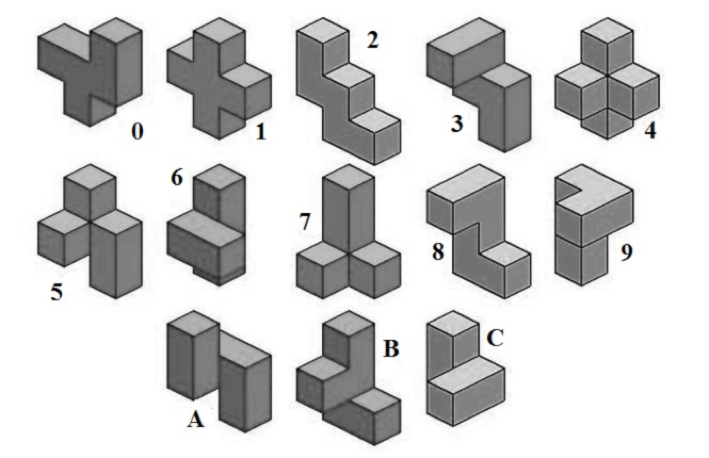
Profesor Hoffmann En 1893, el profesor Hoffmann[1] publicó en Londres sus Puzzles Old and New en los que introdujo un rompecabezas, el «cubo diabólico», formado por seis piezas con las que se puede construir un cubo 3x3x3.
Puzzles Old and New, p. 108 Dichas piezas están formadas por 2, 3, 4, 5, 6 y 7 cubos unitarios, tal como puede verse en la figura adjunta.
Las seis piezas del «cubo diabólico» En la páginas 142 y 143 del mismo libro, Angelo John Lewis propuso la siguiente construcción del cubo.
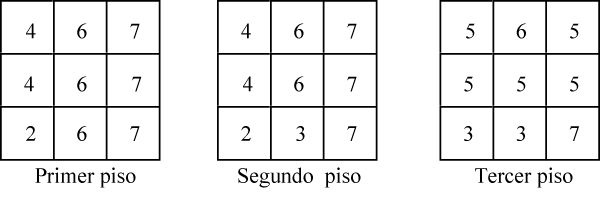
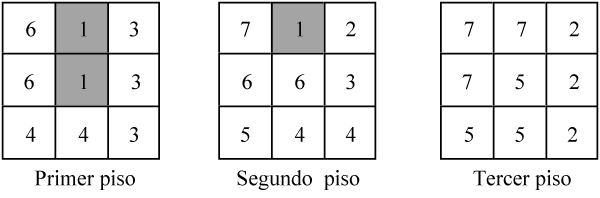
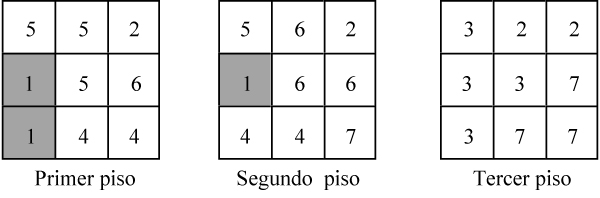
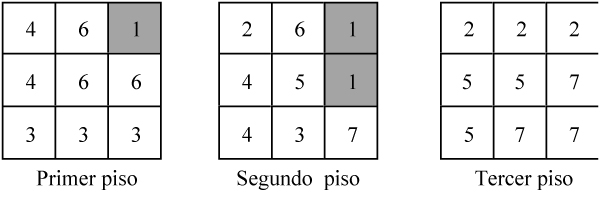
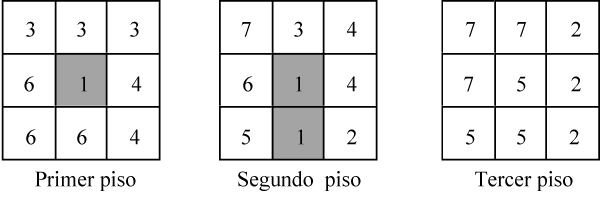
Se colocan las piezas c [= 6], a [= 7] y e [= 4] una al lado de otra tal como se indica en la figura anterior. Acto seguido, la pieza f [= 2] se acopla delante de la e. Después, la pieza d [= 3] se sitúa entre a y f, completando una cara del cubo. Por último, en los espacios vacíos que quedan, se coloca la pieza b [= 5]. Para describir la construcción anterior de forma más precisa, utilizaremos tres cuadrados 3x3 que, escritos de izquierda a derecha, representan el primer, segundo, y tercer piso del hexaedro. Además, en cada cuadrícula escribiremos el número de la pieza que se apoya en él.
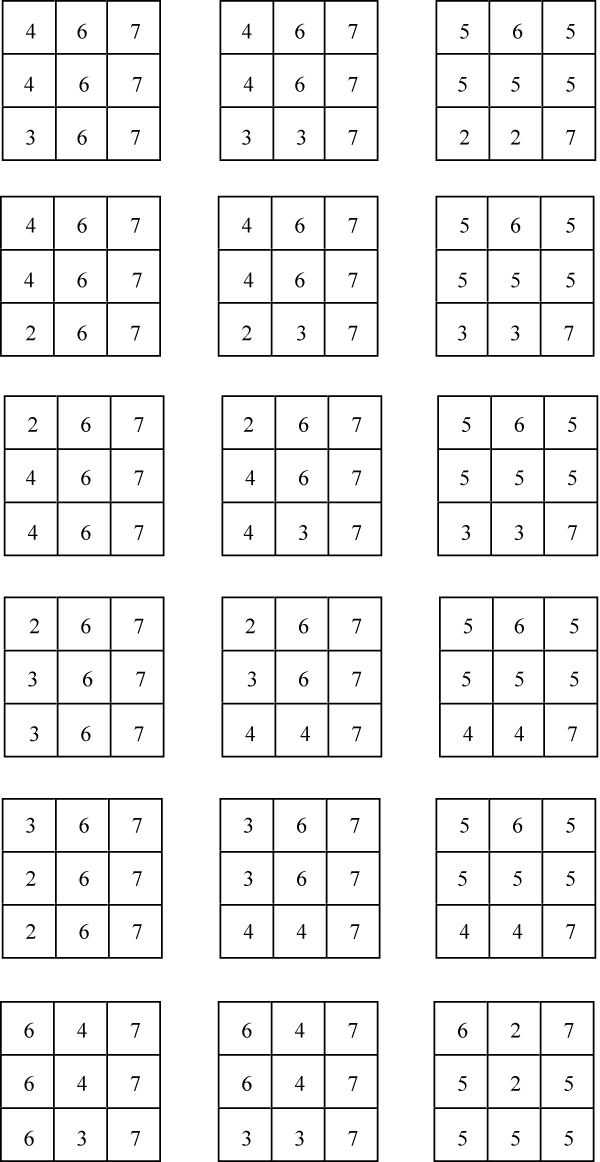
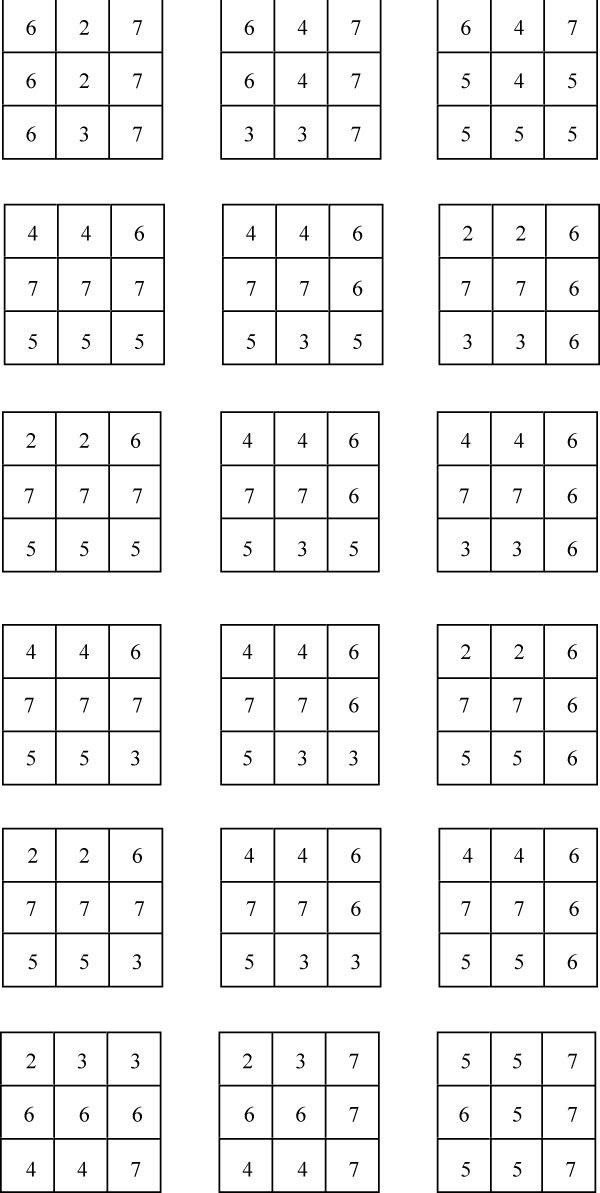
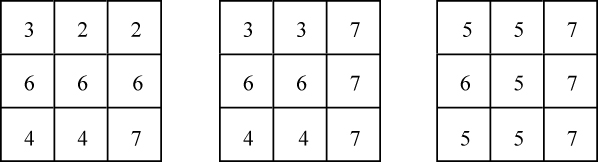
Hay trece formas diferentes de construir un cubo 3 3 3 con las seis piezas del «cubo diabólico». Las presentamos con la ayuda del código que acabamos de describir. Notemos que la segunda de ellas es la propuesta por Hoffmann.
2. El cubo SOMA2.1. El puzleEl rompecabezas tridimensional SOMA fue ideado por el poeta, filósofo, matemático y científico danés Piet Hein.
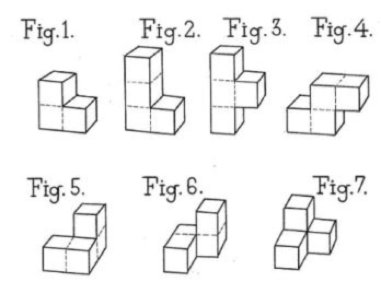
Piet Hein (1905 – 1996) Al parecer, la idea le surgió durante una conferencia sobre Física Cuántica. En la patente inglesa del SOMA, fechada el 19 de marzo de 1934, leemos: Mi invento se ilustra en los dibujos adjuntos, en los que: Las figuras 1-7 son dibujos en perspectiva de las siete piezas.
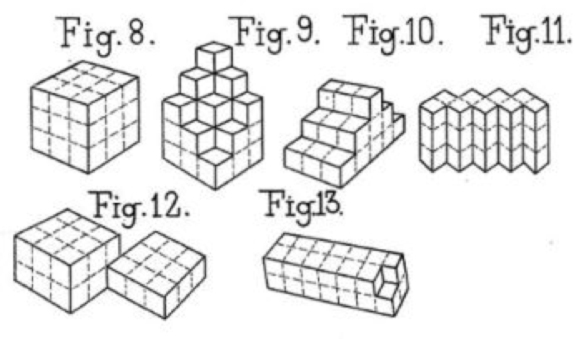
Las figuras 8-13 son ejemplos de cuerpos o figuras geométricas sólidas que se pueden construir con las siete piezas.
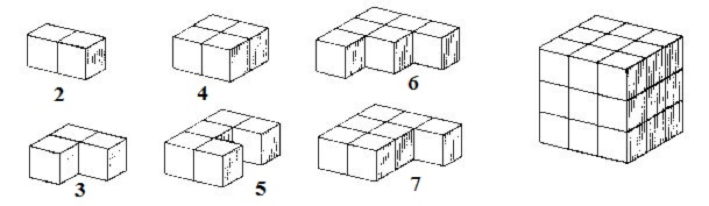
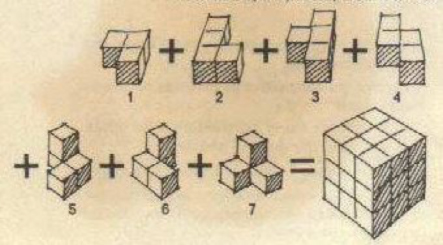
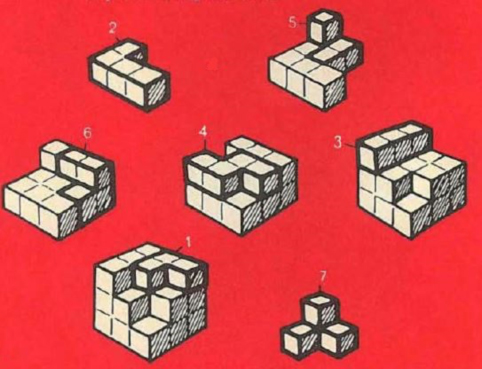
Cada una de las piezas de las figuras 1-7 se componen de tres o cuatro cubos yuxtapuestos. La pieza 1 está formada por tres cubos, mientras que cada una de las restantes está compuesta por cuatro cubos dispuestos de diferentes formas. El conjunto de todas las piezas equivale a veintisiete cubos.
2.2. El problema fundamentalCon las siete piezas del SOMA, se puede generar un sinfín de objetos 3D.
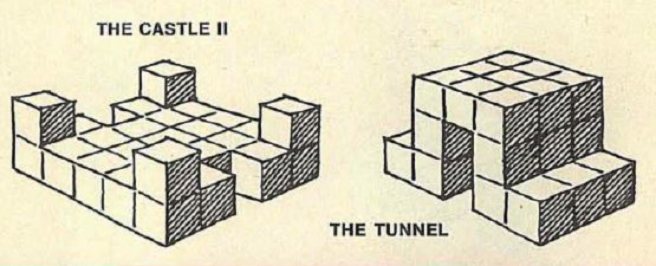
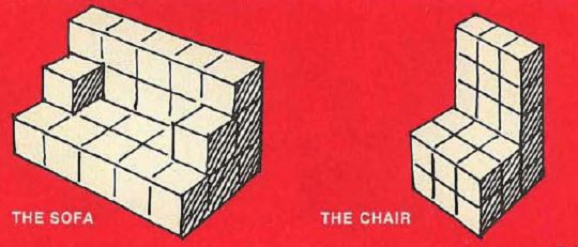
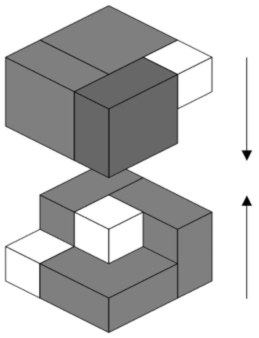
Objetos 3D que se pueden construir con el SOMA. Además, se puede construir un cubo 3x3x3 («problema fundamental»).
Ilustración del manual del SOMA (p. 4) En 1961, los matemáticos de la Universidad de Cambridge John Horton Conway y Michael J. T. Guy (1942) obtuvieron manualmente las 240 formas distintas de hacerlo.
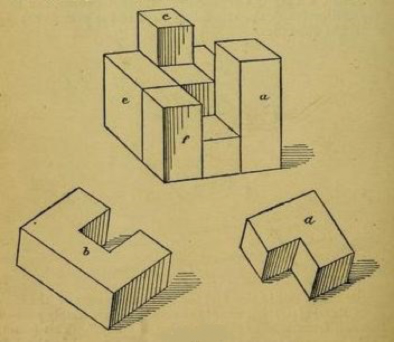
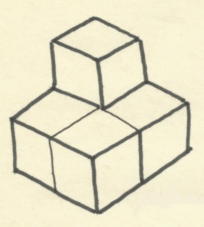
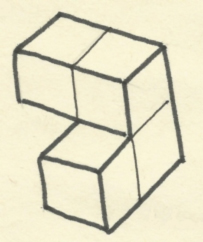
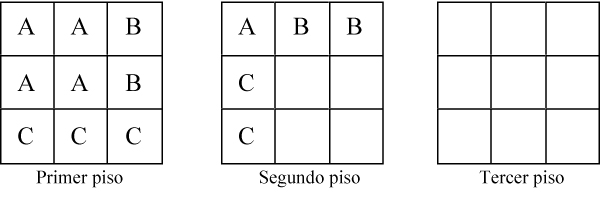
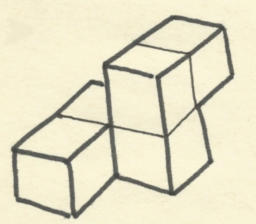
John Horton Conway (1937) En la figura adjunta reproducimos una posible solución del «problema fundamental»
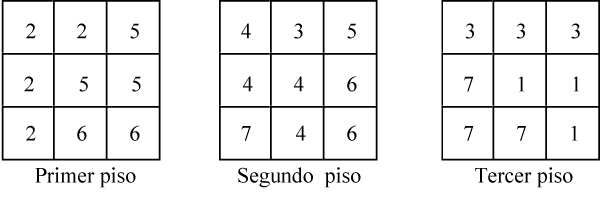
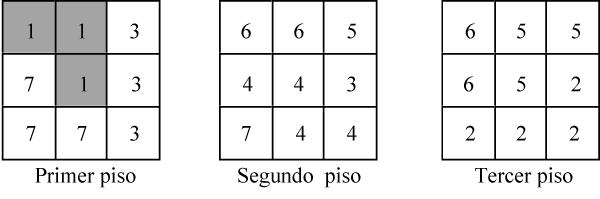
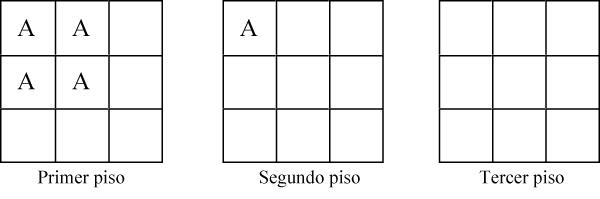
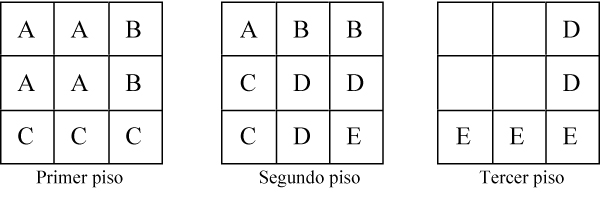
Construcción del cubo con las siete piezas del SOMA[3] Utilizando el código descrito en el parágrafo 1, la construcción anterior se convierte en:
2.3. Jugando con el SOMACon dos juegos SOMA, dos jugadores pueden poner a prueba su habilidad tridimensional en un torneo intelectual que se ajusta a las siguientes reglas:
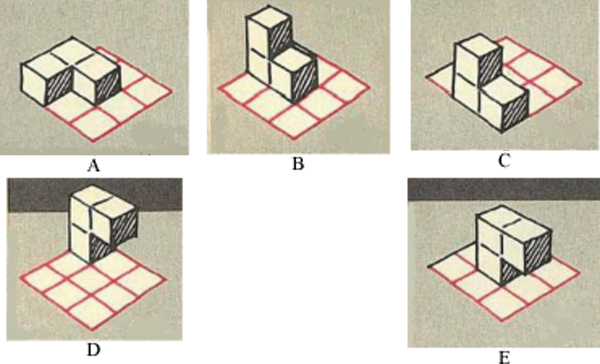
Los siguientes dibujos de Piet Hein muestran algunas posiciones teóricas de partida para la pieza 1.
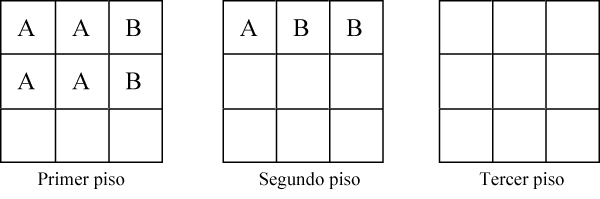
Proponemos algunas construcciones del cubo a partir de dichas posiciones. POSICIÓN A
POSICIÓN B
POSICIÓN C
POSICIÓN D
POSICIÓN E
3. El cubo de Mikusinski
Jan Geniusz Mikusinski (1913 – 1987) El matemático polaco J. G. Mikusinski obtuvo la siguiente disección del cubo en seis policubos.
Las seis piezas del «cubo de Mikusinski» El «cubo de Mikusinski» también se conoce como «cubo de Steinhaus» dado que apareció por primera vez, que sepamos, en el libro Mathematical Snapshots (1950) del matemático y pedagogo polaco Hugo Steinhaus.
Hugo Steinhaus (1887 – 1972) La reconstrucción del cubo con dichas piezas sólo admite las dos soluciones que se muestran en la figura siguiente.
4. Disecciones del cubo en piezas idénticas4.1. El cubo de O’BerineAtendiendo al testimonio de Martin Gardner (Rosquillas anudadas, p. 33), se debe al escocés Thomas H. O’Berine la disección de un cubo en nueve «tricubos» como el de la figura adjunta.
Según el divulgador norteamericano: Los intentos de atinar por tanteo a construir un cubo con los nueve tricubos pueden resultar verdaderamente exasperantes, salvo que, por fortuna se haya acertado en un procedimiento sistemático. ¿Cómo descubrir dicho procedimiento sistemático? En primera instancia, notemos que con dos tricubos se puede construir una estructura [= 2TC] como la del diagrama siguiente.
Por consiguiente, con seis tricubos se pueden construir tres. Acto seguido, dispongamos los tres tricubos restantes tal como se detalla a continuación.
A partir de aquí, añadiendo sucesivamente las tres estructuras 2TC a la «escalera» anterior, se puede completar un cubo 3x3x3 siguiendo las indicaciones de la figura adjunta.
4.2. Un cubo grande: el Gridlock PuzzleEl Gridlock Puzzle es un rompecocos 3D compuesto por cincuenta y cuatro piezas como las de la figura adjunta.
El objetivo que se persigue es el de construir un cubo 6x6x6 con todos los tetracubos del rompecabezas. Para conseguirlo, basta con construir (utilizando dieciocho piezas) dos capas del cubo superpuestas [= paralelepípedo 6x6x2], tal como se detalla en los diagramas adjuntos.
Repitiendo este proceso dos veces más se consigue materializar el cubo con todas las piezas del puzle. 5. El puzle de Slothouber-Graatsma
William Graatsma (1925) y Jan Slothouber (1918 – 2007) Se debe a los arquitectos holandeses Jan Slothouber y William Graatsma un puzle formado por seis bloques 1x2x2 y tres bloques 1x1x1 con los que se puede formar un cubo 3x3x3. La solución es única, salvo simetrías y rotaciones, y se comprende fácilmente a partir del esquema siguiente.
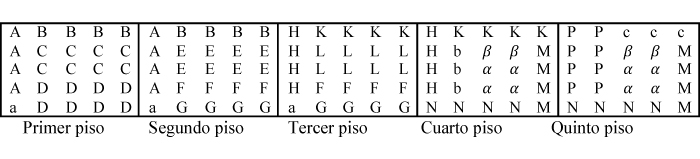
6. El cubo de ConwayJohn Horton Conway, del que ya hemos hablado en el parágrafo 2.2., diseñó un puzle compuesto por las dieciocho piezas siguientes:
Con ellas se debe formar un cubo 5x5x5.
Los cuatro tipos de bloques Designando los trece bloques 1x2x4 por A, B, C, D, E, F, G, H, K, L, M, N y P, los tres bloques 1x1x3 por a, b y c, el bloque 2x2x2 por α, y el bloque 1x2x2 por β, una posible construcción del cubo requerido es:
7. El cubo de BedlamAcabamos este catálogo de rompecabezas hexaédricos con un puzle compuesto por trece piezas (doce pentacubos y un tetracubo), cuyos bocetos adjuntamos.
Su creador es el británico Bruce Bedlam.
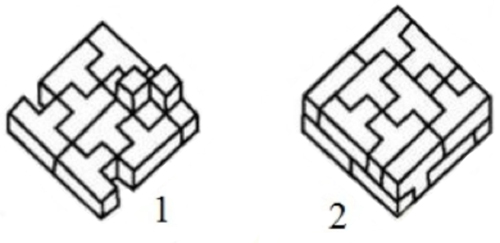
Bruce Bedlam Con las trece piezas se puede montar un cubo 4x4x4 de 19186 formas diferentes. El reto de conseguir una no es fácil y se necesita una gran dosis de paciencia, organización y constancia.
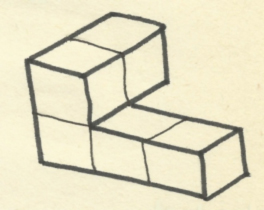
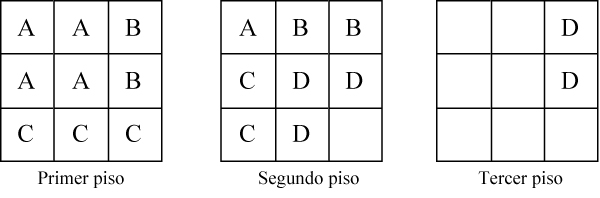
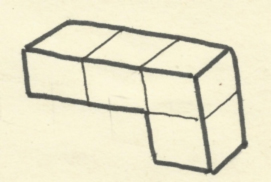
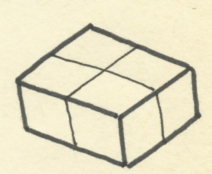
Una solución al cubo de Bedlam 8. Fábrica de rompecabezas cúbicosEn las secciones precedentes hemos presentado varios puzles cúbicos sin prestar atención al procedimiento que pudieron seguir sus inventores a la hora de diseñarlos. Desde una óptica formativa, esta fase de creación resulta particularmente interesante. Por este motivo, en este último parágrafo (a modo de anexo), ofrecemos el alumbramiento de un «nuevo» rompecabezas hexaédrico. Un puzle 3x3x3 con seis piezas[1] Empezamos con un pentacubo A, cuatro de cuyos cubos ocupan el primer piso y uno ocupa el segundo.
La apariencia tridimensional de A se ajusta al boceto siguiente.
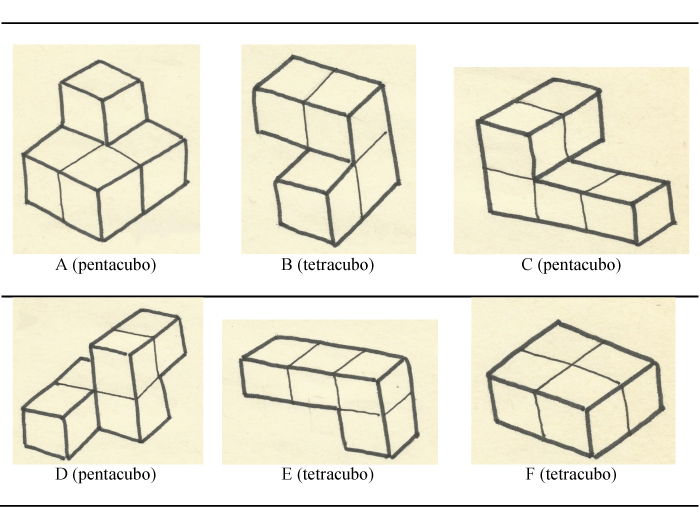
[2] Proseguimos con el tetracubo B, dos de cuyos cubos ocupan el primer piso y los dos restantes ocupan el segundo.
En la figura siguiente se ofrece una representación en perspectiva de B.
[3] En tercer lugar, concebimos el pentacubo C, tres de cuyos cubos ocupan el primer piso y los dos restantes el segundo.
En el boceto adjunto se muestra una representación de C.
[4] Acto seguido «creamos» el pentacubo D, tres de cuyos cubos están en el segundo piso y los dos restantes en el tercero.
En la figura siguiente ofrecemos una representación de D.
[5] Incluimos ahora el tetracubo E que tiene un cubo en el segundo piso y tres en el tercero.
La representación 3D de dicho policubo se ofrece en el boceto siguiente.
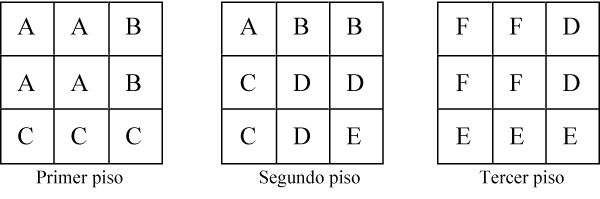
[6] Habiendo llegado a este punto, los huecos que quedan por cubrir sólo se pueden llenar con el tetracubo F.
La figura adjunta es una representación plana del policubo F.
Con esto, acabamos de «inventar» o «reinventar» un rompecabezas cúbico de seis piezas (tres tetracubos y tres pentacubos).
Referencias bibliográficasGARDNER, M. (1987). Rosquillas anudadas y otras amenidades matemáticas. Barcelona: Editorial Labor, S. A. HOFFMANN, P. (1893). Puzzles Old and New. London: Frederick Warne and Co. MEAVILLA SEGUÍ, V. (2011). El lobo, la cabra y la col. Córdoba: Editorial Almuzara, S. L.
Referencias onlineCubic Block Puzzles. The 3x3x3 Cube
Notas:[1] Pseudónimo del inglés Angelo John Lewis (1839 – 1919). [2] Parker Brothers distribuyó el SOMA en Estados Unidos. El manual editado por dicha empresa fue escrito e ilustrado por Piet Hein (Introducing SOMA, 1969). |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |