 Fractales, sello a sello
Fractales, sello a sello |
 |
 |
 |
|
Heraldo de Aragón, 28 de Julio de 2020 También los fotogénicos fractales, esos objetos geométricos cuya estructura se repite a diferentes escalas, están presentes en la filatelia.
Sello emitido en Macau en 2005 y dedicado al Conjunto de Mandelbrot
¿Cuánto mide la costa de Gran Bretaña? Con esta pregunta de apariencia sencilla, Benoît Mandelbrot titulaba en 1967 un artículo científico que ponía de manifiesto la existencia de contornos (las costas geográficas) cuya medida dependía del instrumento utilizado para medir. Aparecen así curvas, como el copo de Koch, que tienen dimensión fraccional superior a 1. Su construcción iterativa la podemos ver en el sello de Macau. 
Copo de Koch en estos sellos suecos (2000)
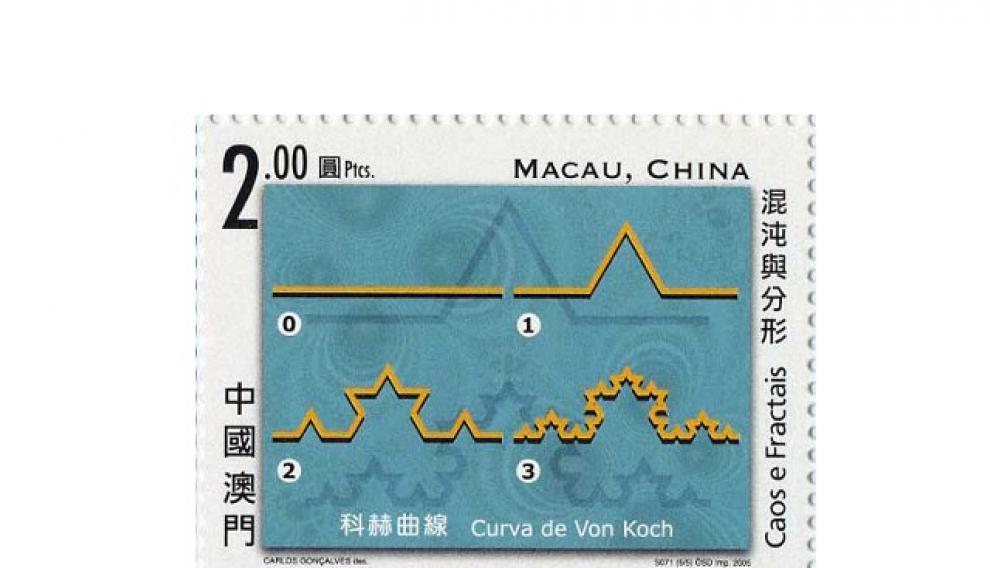
Macau, 2005 Estos objetos cumplen una propiedad llamada autosimilitud o autosemejanza, es decir, todo el objeto es exactamente o aproximadamente similar a una de sus partes. Dicho de otro modo, al hacer zoom sobre el objeto vemos lo mismo que antes de hacer el zoom. El nombre matemático para estos objetos es fractal. Así, un fractal es un objeto geométrico cuya estructura se repite a diferentes escalas. La propiedad matemática que lo define es que su dimensión fractal es un número racional mayor a su dimensión topológica (1 para líneas o 2 para figuras planas).La dimensión fractal de la curva de Koch es log(4)/log(3) (aproximadamente 1,2618) y la de la curva de Hilbert es 2. 
La curva de Hilbert en un sello emitido en Macau en 2005 Hay dos ejemplos de fractales clásicos que no cumplen la definición anterior: el conjunto de Cantor y el triángulo de Sierpinski. Sus dimensiones fractales son log(2)/log(3) <1 y log(3)/log(2) < 2, respectivamente. 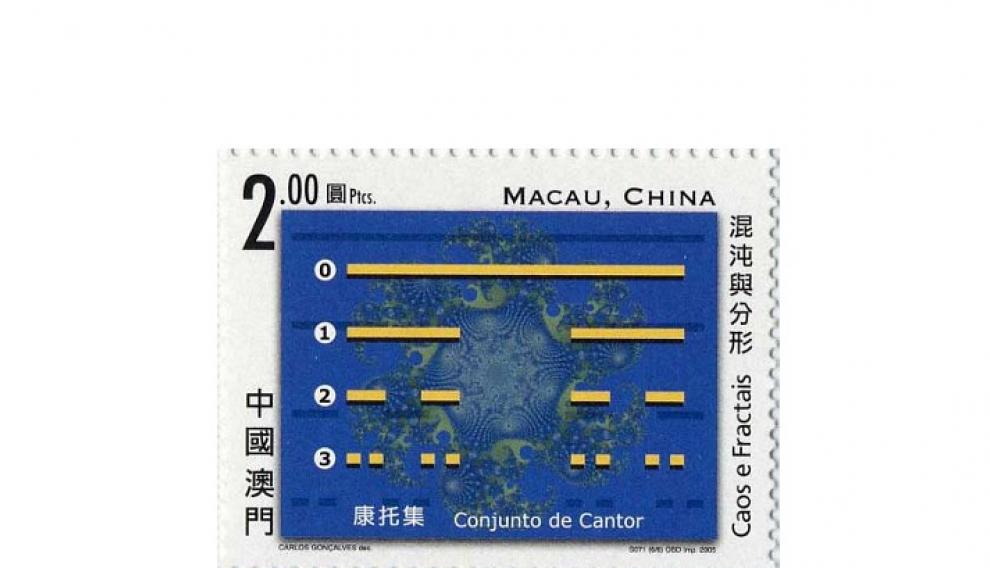
Conjunto de Cantor en un sello emitido en Macau en 2005 
Sierpinski y su triángulo en sellos de Polonia (1982) y Macau (2005)
Como muestran los ejemplos anteriores, el concepto de iteración está muy unido al de fractal. Otro tipo de fractales, los llamados conjuntos de Julia y los conjuntos de Mandelbrot, surgen de la iteración de funciones cuadráticas definidas en el plano complejo. 
Sellos de España (2001) e Italia (2000) 
Israel (1997) La fractalidad también está presente en la naturaleza aunque no de manera infinita por los propios límites de la materia. Las nubes, los copos de nieve o el sistema circulatorio serían algunos ejemplos que cumplen la propiedad de invarianza a determinadas escalas. En los sellos de Estados Unidos se muestran imágenes de copos de nieve reales recogidos en Alaska, Michigan y Ontario. 
Sellos de Estados Unidos (2006) y Hungría (1973) La propiedad de autosimilitud de los fractales tiene importantes aplicaciones en la técnica y la tecnología. Por ejemplo, en la animación por ordenador, donde a partir de la repetición de una sencilla instrucción se pueden crear árboles o montañas. 
Macau (2005) y Estados Unidos (2015) |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |







