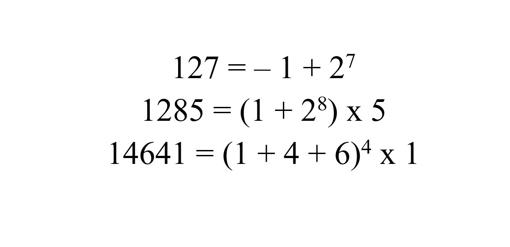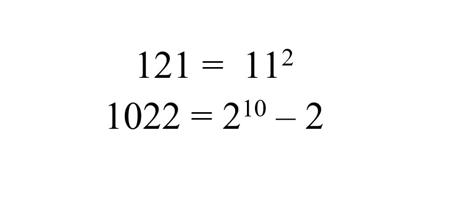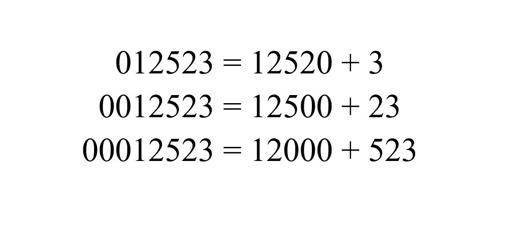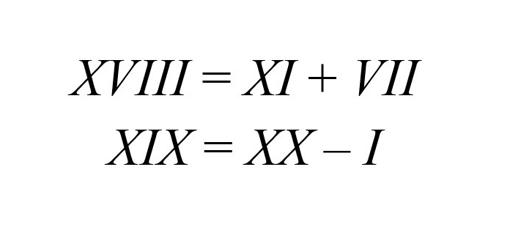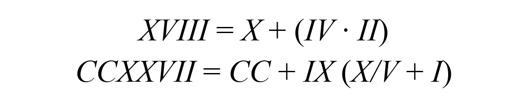Los números de Friedman, cuando los números están dentro de los números
Los números de Friedman, cuando los números están dentro de los números |
 |
 |
 |
|
ABC, 2 de Noviembre de 2020 Son números enteros que puedan expresarse con los dígitos con los que están formados utilizando las operaciones aritméticas básicas
Entre las muchas citas que uno escucha sobre casi cualquier asunto (normalmente con el suficiente ingenio como para llamar la atención y alguna parte de verdad que redondeé la frase y nos haga reflexionar o, al menos, para que esbocemos una sonrisa) en alguna ocasión he leído u oído que las matemáticas es la disciplina en la que las cosas o son útiles o son divertidas. La construcción disyuntiva de la sentencia implica que no pueden darnos algo útil y a la vez divertido (algo que no comparto, pero de esto podemos hablar otro día). Hoy voy a contarles algo entretenido, más que divertido, y por ahora, completamente inútil (de modo que los aficionados al estoparaquésirve, vayan pensando otra pregunta más original): los números de Friedman. Se han bautizado con ese nombre a aquellos números enteros que puedan expresarse con los dígitos con los que están formados utilizando las operaciones aritméticas básicas (suma, resta, multiplicación y división) junto a las potencias y los paréntesis. Por ejemplo:
Si nos fijamos un poco, los dígitos aparecen en el segundo miembro en el mismo orden que su expresión decimal. No es necesario para que sea un número de Friedman. En otras palabras, también son números de Friedman:
Estaremos no obstante de acuerdo en que quedan mejor en el mismo orden. Por ello se les ha añadido en ese caso el calificativo de simpáticos: números de Friedman simpáticos. También he visto el adjetivo agradables. No sé muy bien a quien se debe esa expresión (en el original en inglés se denominan, nice Friedman numbers; quizá yo sea un poco «soso» pero considero, en ambos idiomas, que una expresión más acorde sería la de números de Friedman propios, pero, en fin, como se suele decir, doctores tiene la Santa Madre Iglesia). ¿Lo hemos entendido? ¿Seguro? Obsérvese en los dos ejemplos anteriores que pueden utilizarse números de más de una cifra, con tal de que sus dígitos sean del número inicial. Así para el 121 podemos utilizar el 11, o para el 1022 la potencia 10. Lo que no se puede es poner ceros delante del número, porque entonces cualquier número sería de Friedman. El 24, por ejemplo, podríamos ponerlo como 024 = 20 + 4. Entonces podríamos hacer esa jugada con cualquier número porque bastaría con añadir tantos ceros delante como nos hicieran falta para descomponerlo en suma:
Y así sucesivamente, de modo que no vale poner ceros por delante. Bien, esto aparentemente no es más que un pasatiempo, con el que «entretener» a los alumnos para que practiquen un poco el cálculo y las operaciones (¿o quizá no?). Pero como los matemáticos no podemos dejar las cosas en algo tan «trivial», podemos empezar a hacernos preguntas. Por ejemplo, ¿existen infinitos números de Friedman, o sólo son un capricho curioso de unos pocos números? ¿Cómo podemos demostrar que hay, o no, infinitos? En realidad, aunque lo parezca, resolver esa cuestión no es demasiado complicado…, si han entendido bien la pregunta, porque en matemáticas muchas veces nos obcecamos con lo que creemos entender y no con lo que en realidad es. Probar que existen infinitos números de Friedman no quiere decir «encontrarlos todos» (entre otras cosas porque si son realmente infinitos, nunca terminaríamos, salvo que pudiéramos describirlos con una fórmula). Nos bastará con encontrar una expresión que agrupe a infinitos de ellos, aunque no sean todos. Y esa expresión existe y alguien la ha encontrado y nos la ha legado:
para todo n > 0. Está claro que el número n es tan grande como queramos (puede tomar infinitos valores, por tanto), y que 161051 es igual que 11^5". En el segundo miembro se han utilizado los tres unos, el seis, el cinco, pero, ¿por qué esa suma de ceros? Si n = 1, el número es:
Si cuentan el número de ceros que aparecen (para eso les he incluido una separación cada tres dígitos), son 18 x 3 + 1, o sea 55. En la expresión del segundo miembro, recopilemos, tenemos los dígitos n, los tres unos, el seis, el cinco y cuatro ceros. Están todos, salvo 51 ceros más, que añadimos en forma de suma. Para valores más grandes de n, puede que aparezcan más ceros, pero no importa porque podemos añadir todos los que nos hicieran falta con ese truco tan elemental. Vale, hay pues infinitos números de Friedman, ..., en base diez. ¿Ocurrirá lo mismo en otras bases? Por ejemplo, en base dos, ya saben, sólo con ceros y unos. Veamos el siguiente número:
Recuerden que estamos en base dos, y las operaciones debemos hacerlas asimismo en binario, no en base decimal. Así, en el segundo miembro, 1 + 1, ¿cuánto es? No, 2 no, porque sólo tenemos ceros y unos. Alguien dirá: como 2 es igual a 0 en base dos, pues entonces es 0. Tampoco. Es 10, porque 2 en base binaria se escribe 10 (ya saben, 1 x 2 + 0 x 2^0). Vamos con el exponente, 111. En base dos es 111; en base decimal es:
O sea, el número 7. Las posiciones de unidades, decenas, centenas, etc., van multiplicadas por las sucesivas potencias de 2. Seguro que tienen esto un poco olvidado, ¿verdad? Esto de la base binaria es cómo los ordenadores interpretan todo. No me digan que una ignorante máquina se maneja mejor que ustedes, porque no debería ser así. A las máquinas, en lo único que debemos permitirles que nos superen es en velocidad (que para eso están), pero en nada más. En fin, sigamos. Hagamos la siguiente operación:
Piensen en modo decimal, pero luego escríbanlo en binario; es lo mejor para no liarse. Como 111 en binario es el 7 en decimal, estamos elevando 10 a la séptima potencia, por tanto, el resultado es el uno y siete ceros. Continuando con la operación que nos traemos, ¿y cuánto es 10000000 – 1? Pensemos, como les he dicho, en el número en modo decimal.
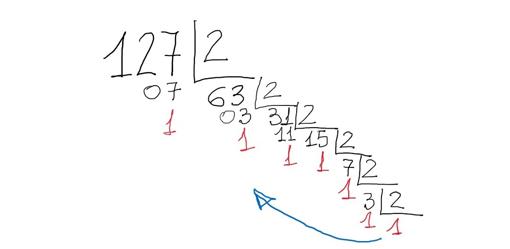
O sea que es el número 128 en base decimal. Y 128 – 1 = 127. ¿Y cómo es 127 en base binaria? Recordemos también cómo se obtenía el número en binario a partir de la notación decimal. En este caso tenemos que dividir por 2:
El número en base dos está formado por todos los restos que se obtienen (aparecen en color rojo) junto al último cociente, empezando por éste último y siguiendo el sentido de la flecha azul). Por tanto 127 en binario es 1111111. Y por eso la operación del segundo miembro es idéntica en binario a la del primer miembro, es decir:
Si repasan el inicio de esta reseña, resulta que, en decimal:
Es decir que, 127 es un número de Friedman simpático, ¡¡¡tanto en base decimal, como en base dos!!! Además, 127 es el primer número de Friedman que es primo (todos los anteriores son compuestos). Seguramente a estas alturas, ustedes mismos se estén haciendo ya otras preguntas: ¿existen infinitos números de Friedman primos? ¿Existen infinitos números de Friedman en base dos? ¿Y en otras bases? Pues sin querer abrumarles más de la cuenta, se pueden hacer otras muchas preguntas: ¿existen sucesiones de enteros consecutivos de Friedman? ¿Cuál es la más larga? Si elegimos un número al azar, ¿cuál es la probabilidad de que sea un número de Friedman? ¿Hay números de Friedman sin ceros en su expresión? ¿Y que tengan los diez dígitos una única vez? ¿Y con todos los dígitos iguales? ¿Conocen los números vampiros, variedad particular de los números de Friedman? Perfectamente se puede escribir un libro y bastante grueso hablando sólo de este tipo de números (igual que con cualquier otro asunto matemático). La persona que ha dado nombre a estos números, es un profesor jubilado de matemáticas de la Universidad Stetson de Florida (EE. UU.), Erich Friedman, al que le apasionan los juegos matemáticos (sobre todo los que pueden construirse en madera; no sé si saben que a esta parte de la matemática recreativa se la llama metagrobología; les hablaré de ello en otro artículo, que es muy divertido). El propio Friedman ha propuesto también los llamados números Anti-Friedman como aquellos números que no tienen dígitos repetidos y pueden formarse usando todos los dígitos no presentes en el número original, pudiendo usarse las mismas operaciones de los números de Friedman, es decir, suma, resta, multiplicación, división, exponenciación y concatenación. Por ejemplo, 10752 sería un número Anti-Friedman, porque puede expresarse con todos los dígitos que no aparecen en él:
De éstos, de momento, se sabe menos. El más grande encontrado hasta ahora es:
Si los Romanos levantaran la cabezaFriedman también se planteó la idea de si utilizando notación de números romanos, podrían componerse números de Friedman (como ven no sólo los Romanos están locos que diría Obélix; por cierto, no me resisto a contarles, a lo mejor ya lo saben que, esa frase, en italiano es Sono Pazzi Questi Romani, cuyas iniciales componen SPQR, que ya sabrán que es. Goscinny nunca dejará de sorprendernos). La sorpresa es que todos los números romanos con más de una letra son números de Friedman. Y para ello basta con sumas, ocasionalmente alguna resta, y el re-orden adecuado. ¿Quieren probar?
Pero todos ellos son demasiado triviales (a la altura precisamente de los Romanos ideados por Goscinny). Por eso los aficionados a estos pasatiempos, buscan expresiones lo más complejas posibles, con productos, divisiones, exponenciaciones, mejor que simples sumas y restas. Por ejemplo, el anterior XVIII prefieren describirlo como:
Ninguno de los propuestos es número romano de Friedman simpático. ¿No los hay? Pues sí, si los hay. A ver si encuentran alguno. Les dejo como curiosidad, para terminar por hoy, el único número de Friedman simpático que contiene todos los dígitos, salvo el cero, que se conoce. (Anímense a ver si encuentran otro).
Alfonso J. Población Sáez es profesor de la Universidad de Valladolid y miembro de la Comisión de divulgación de la RSME. El ABCDARIO DE LAS MATEMÁTICAS es una sección que surge de la colaboración con la Comisión de Divulgación de la Real Sociedad Matemática Española (RSME) |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |