ABC, 19 de Abril de 2021
CIENCIA - El ABCdario de las matemáticas
Pedro Ramos Alonso

Desarrollaron una forma de enseñar matemáticas que pudieron trasladar a sus aulas con los excelentes resultados

Niños de primaria en una clase en Singapur - Reuters

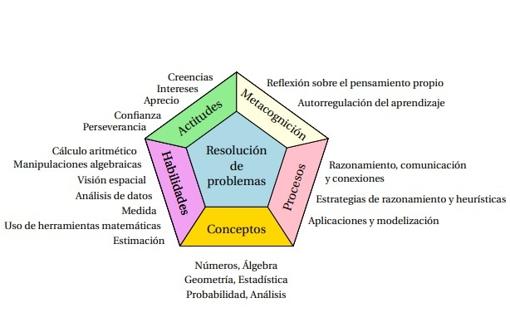
Singapur era hace 50 años un país en vías de desarrollo, sin recursos naturales. A finales del siglo XX empezó a encabezar los resultados de las pruebas internacionales más conocidas, como PISA, TIMSS o PIRLS, tanto en matemáticas como en ciencias o lengua. Al progreso educativo le han acompañado el progreso económico, y Singapur es en nuestros días uno de los países más ricos del mundo. Aunque no es fácil analizar por completo las razones de este progreso económico, existe una opinión bastante extendida de que el éxito en educación ha tenido un papel fundamental. En este progreso educativo existen con seguridad razones sociológicas (como la valoración oriental del trabajo y el saber) pero también puramente educativas (elegir bien qué enseñar y cómo enseñarlo). En particular, esto es cierto en matemáticas, que es el área en la que comenzaron sus reformas a comienzos de los años 90.

La enseñanza de las matemáticas en Singapur hace 50 años era tradicional, y sus resultados, modestos. Según Yeap Ban Har, una de las figuras más conocidas, a nivel internacional, en la divulgación de este enfoque de la enseñanza de las matemáticas, estos son los errores que cometían en su país en aquellos años: demasiados cálculos tediosos y largos, cuya utilidad en estos tiempos es cuestionable; aprendizaje de procedimientos sin comprensión; excesivo uso del aprendizaje memorístico.

Aunque es complicado generalizar, sí creemos que estas prácticas están bastante extendidas en la forma en que se enseñan y aprenden matemáticas en nuestras aulas. Así se refleja en los estudios internacionales antes mencionados, donde nuestros alumnos muestran ser capaces de resolver las cuestiones básicas, de carácter repetitivo, pero tienen muchas más dificultades cuando se enfrentan a tareas de mayor demanda cognitiva, como el razonamiento y la resolución de problemas no rutinarios.

La reforma que se desarrolló en Singapur durante los años 80 dio lugar a lo que ahora se conoce en los países de nuestro entorno como 'Matemáticas Singapur' aunque, como sus promotores reconocen, «no hay nada de Singapur en esas matemáticas». Los principios en los que se basa esta metodología son occidentales, y bien conocidos en el área de Didáctica de las Matemáticas. Lo que hicieron en Singapur fue una síntesis de estos principios, y basados en ellos desarrollaron una forma de enseñar matemáticas que pudieron trasladar a sus aulas con los excelentes resultados que hemos mencionado.

En Singapur consideran la resolución de problemas como el objetivo central del aprendizaje de las matemáticas, y este hecho está muy bien resumido en la imagen (de elaboración propia, a partir de la que figura en la documentación del Ministerio de Educación de Singapur): los conceptos, las habilidades, las actitudes, los procesos y la metacognición son fundamentales, pero todos estos componentes del proceso de aprendizaje tienen un objetivo común: la resolución de problemas.

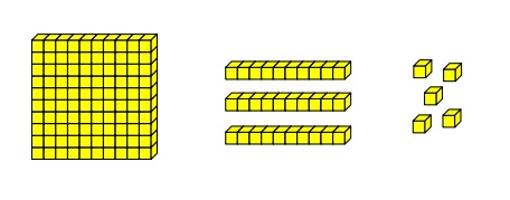
Las características de este enfoque de enseñanza de las matemáticas se aprecian mejor en las primeras etapas, en la Educación Primaria. Es en esta etapa donde varios de los principios metodológicos que ahora expondremos tienen más importancia, y donde los resultados de Singapur en las pruebas internacionales son más llamativos. En la prueba de TIMSS de 4º de Educación Primaria, el liderazgo de Singapur es cada vez más claro. En particular, resulta muy llamativa la cantidad de sus alumnos que llegan al máximo nivel en la prueba, denominado «Avanzado», y que muestra que los alumnos son capaces de resolver problemas no rutinarios. Mientras que en el conjunto del estudio el 7 % de los alumnos alcanzan este nivel, en el caso de Singapur la cifra es del 54 %. Su liderazgo en este aspecto es especialmente llamativo, pues le siguen Hong Kong con el 38 % y la República de Corea con el 37 %. En este indicador nuestros resultados son especialmente preocupantes, pues solo un 4 % de nuestros alumnos alcanzaron ese nivel de resultados. Creemos que este contraste ya es suficiente para conjeturar que el enfoque de la enseñanza de las matemáticas que utilizan en Singapur en esas etapas educativas está generando un buen aprendizaje.

Vamos a intentar dar una descripción rápida de los principios metodológicos que están en la base de las 'Matemáticas Singapur'. Despues daremos algún ejemplo concreto de cómo se pueden aplicar estas ideas en la enseñanza de las matemáticas de primaria.

Seguramente la idea más importante es la del aprendizaje en tres etapas, debida a Jerome Bruner: para que los alumnos puedan entender un nuevo concepto matemático deben empezar con una primera fase manipulativa, en la que se utilizan materiales concretos; la segunda etapa debe ser gráfica, y en ella se representa la información; finalmente, en la tercera, la simbólica, es donde las ideas anteriores se formalizan para llegar al lenguaje matemático tradicional.

Por ejemplo, si queremos que los alumnos adquieran sentido numérico y comprendan la notación posicional, es fundamental que tengan la ocasión de contar en situaciones diversas, y de utilizar materiales como los bloques de base 10 de la imagen, diseñados para ayudar a entender que un grupo de 10 unidades forma una decena, y que 10 decenas forman una centena.

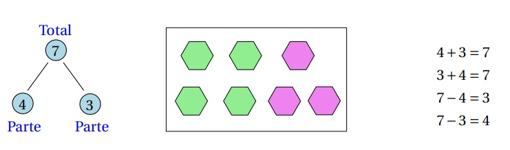
Richard Skemp fue un matemático británico que se interesó en la educación matemática, y que por ello cursó también estudios de psicología. Una de las contribuciones más relevantes de Skemp al desarrollo de la educación matemática fue la distinción entre comprensión instrumental y comprensión relacional. Cuando un alumno afirma que entiende cómo se dividen dos fracciones, porque las multiplica en cruz, está mostrando comprensión instrumental, conoce el procedimiento. La comprensión relacional (es tentador calificarla como la comprensión real) requiere que el alumno comprenda el significado de la operación y que sepa relacionarla, por ejemplo, con la división de números naturales que ha estudiado en cursos anteriores.

Richard Skemp afirmó que solo hay auténtico aprendizaje cuando se alcanza esta comprensión relacional, y que aprender los procedimientos sin entender lo que se está haciendo, y sin poder relacionarlo con otros contenidos matemáticos, es algo que debemos evitar. Uno de los principios directores del currículo de Singapur es tratar en cada momento lo que los alumnos puedan comprender, e introducir los diversos procedimientos cuando los alumnos están preparados para comprender su funcionamiento, y dedicando el tiempo suficiente para que puedan alcanzar esa comprensión. Seguramente los docentes que estén leyendo este texto habrán reaccionado ante esta última frase: la falta de tiempo es una de las quejas más frecuentes en nuestro sistema. ¿Qué hicieron en Singapur para disponer de ese tiempo necesario para trabajar los conceptos en profundidad?

1. Una revisión del currículo, eliminando contenidos que consideraban menos importantes. Estudian menos cosas, para poder estudiarlas mejor.

2. Eliminar la repetición de contenidos: cuando algo se estudia en profundidad, se puede repasar, y se debe utilizar más adelante, pero no es necesario volver a estudiarlo. La repetición de contenidos, porque no se han aprendido cuando se vieron anteriormente, es uno de los problemas más frecuentes en nuestras aulas.

Algunas ideas de Lev Vygotski están también entre las más importantes de esta metodología:

1. La importancia del andamiaje y la zona de desarrollo próximo. Es importante diseñar las secuencias didácticas para que las actividades propuestas estén próximas a lo que los alumnos ya conocen. Cada vez que se produce un salto demasiado grande corremos el riesgo de que algunos alumnos no comprendan lo que hacemos, y se vayan quedando rezagados.

2. La relevancia del aprendizaje entre iguales, y la importancia de la verbalización. Sin menoscabo del papel del docente como transmisor de conocimientos, es importante dar oportunidades para que los alumnos verbalicen sus razonamientos. Cuando explicamos lo que hacemos se profundiza nuestra comprensión.

Veamos algunos ejemplos concretos de propuestas didácticas que nos parecen especialmente relevantes, por su importancia en el aprendizaje.

El sentido numérico se suele definir como la comprensión de los números y su significado, sus relaciones, y cómo esto se puede aplicar a calcular de manera flexible y razonada. Las descomposiciones numéricas son seguramente la clave para el desarrollo del sentido numérico y, como ocurría con los fundamentos metodológicos, no son específicas de las matemáticas Singapur. La aportación de esta metodología ha sido su integración en el desarrollo del cálculo. En Singapur hablan de «number bonds» (números conectados) y los representan como se muestra en la imagen. El número conectado permite resumir la situación de la imagen, y ayuda a la conexión de los significados de la suma y la resta, fundamental al comienzo del estudio de estas operaciones.

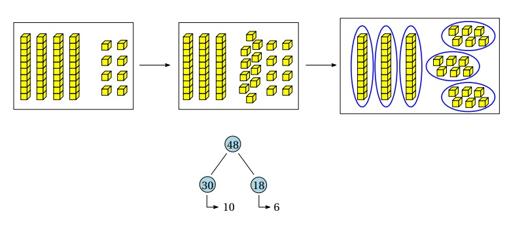
Los números conectados son de gran utilidad para calcular sumas y restas de números de dos cifras, pero vamos a mostrar un ejemplo un poco más avanzado, viendo cómo también se pueden usar para el cálculo de divisiones.

Supongamos que queremos calcular 48 ÷ 3. Si queremos hacer este cálculo sin recurrir al algoritmo tradicional, seguramente la primera alternativa que se nos puede ocurrir es descomponer 48 como 4 decenas y 8 unidades, es decir, 48 = 40 + 8. Sin embargo, esta no es particularmente adecuada para hacer este cálculo, pues 40 no es divisible entre 3. Si hemos trabajado de manera sistemática las descomposiciones numéricas, y si nos ayudamos de las representaciones del 48 con los bloques de base 10, como en la imagen, nos podemos dar cuenta de que 48 también se puede descomponer como se muestra en forma de número conectado, y esta descomposición nos permite terminar la división propuesta: 48 ÷ 3 = 16

Recordemos que el objetivo no es que los alumnos dividan de esta forma durante todo el aprendizaje. La idea de las tres etapas de Bruner es que en la primera etapa los alumnos hacen estos cálculos con ayuda de materiales manipulativos y en una segunda etapa lo representan gráficamente, como hemos hecho aquí. Esto permite que alcancen una comprensión profunda de los procesos involucrados y que en la última fase, la simbólica, sean capaces ya de calcular sin apoyo adicional y comprendiendo el procedimiento.

El modelo de barras es sin duda la herramienta más conocida de la metodología Singapur, y es de gran ayuda en la resolución de problemas. La idea es muy sencilla: las barras son rectángulos, con los que representamos los datos del problema, y las relaciones que hay entre ellos. En la imagen se muestran los modelos que resumen buena parte de los problemas de estructura aditiva que aparecen en los primeros cursos de primaria, en los que tenemos un total, y dos partes. Si conocemos las partes, y nos pregunta el total, será un problema 'de sumar'. Si, por el contrario, conocemos el total y una de las partes, será un problema 'de restar'.

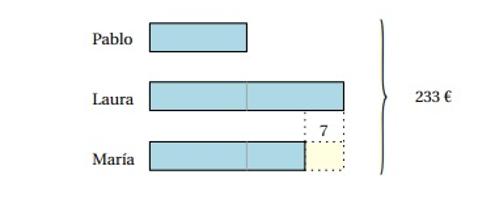
El modelo de barras es una herramienta que se introduce en 2º EP, y que hay que trabajar con paciencia, porque se trata de un cambio significativo en la forma de pensamiento. Hasta ese momento los alumnos han visto las cantidades de forma explícita, y en este momento ven un rectángulo que representa una cantidad en un problema, y otra cantidad completamente distinta en el problema siguiente. Se trata, en definitiva, de empezar a desarrollar el pensamiento prealgebraico, fundamental en el aprendizaje de las matemáticas. No se trata, por supuesto, de una 'receta mágica', pues no todos los problemas aritméticos se pueden resolver con ayuda de este modelo, pero sí es de gran ayuda en buena parte de los problemas que se estudian en la Educación Primaria (además de apoyar la introducción al álgebra en Secundaria, como veremos en un momento). Para terminar, veamos dos ejemplos de problemas de cursos más avanzados donde el modelo de barras muestra su potencial.

Pablo tiene la mitad de dinero que Laura, y María tiene 7 euros menos que Laura. Si entre los tres tienen un total de 233 euros, ¿cuánto dinero tiene cada uno?

En la imagen vemos el modelo de barras que representa la información del enunciado.

A la vista de la imagen, creemos que no es difícil darse cuenta de que, añadiendo 7 euros al total, aparecen 5 rectángulos iguales, por lo que cada uno de ellos representa euros. Con esta información, es inmediato contestar cuánto dinero tiene cada uno.

Este ejemplo también es útil para darse cuenta de cómo el modelo de barras se puede utilizar como introducción al álgebra. Si, guiados por el modelo de barras, llamamos x a la cantidad de dinero que tiene Pablo, entonces Laura tiene 2x y María 2x - 7 . Sumando las tres cantidades, obtenemos la ecuación 2x + 2x - 7 = 233 . El modelo nos sirve, además, para entender cómo podemos resolver esta ecuación: si sumamos 7 en los dos términos obtenemos la ecuación 5x = 40, equivalente a la anterior, pero más sencilla de resolver. Evidentemente, también podríamos haber empezado llamando a la cantidad de dinero que tiene Laura, y en ese caso obtendríamos otra ecuación equivalente a la anterior: x/2 + x + x - 7 = 233.

Para terminar, dejamos propuesto un problema tomado directamente de la prueba que hacen en Singapur al terminar su etapa de primaria. La duración es de 6 cursos, igual que en nuestro país.

El reto, claro, es resolver el problema sin métodos algebraicos.

Luis y Nuria hicieron tarjetas durante dos días. El sábado Nuria hizo 19 tarjetas más que Luis. El domingo, Nuria hizo 20 tarjetas, y Luis hizo 15. Al acabar los dos días, comprobamos que Nuria hizo 3/5 del total de las tarjetas. ¿Cuántas tarjetas hizo Luis?

Pedro Ramos Alonso es profesor Titular del Departamento de Física y Matemáticas de la Universidad de Alcalá de Henares (Madrid) @MsIdeasMnosCtas.

El ABCDARIO DE LAS MATEMÁTICAS es una sección que surge de la colaboración con la Comisión de Divulgación de la Real Sociedad Matemática Española (RSME)