El 'cuadrado mágico de Foz', los 'fozudokus' y las matemáticas llegadas desde Lugo
El 'cuadrado mágico de Foz', los 'fozudokus' y las matemáticas llegadas desde Lugo |
 |
 |
 |
|
ABC, 31 de Mayo de 2021 Un lector del ABCdario de las Matemáticas propone un reto: una variante de los sudokus a la gallega
Cuadrado Mágico de FOZ - Antonio Pomares Olivares
Muchos de los artículos publicados en periódicos y revistas de matemática recreativa (y de otras temáticas) suelen mencionar en ocasiones aportaciones de los lectores, que proponen sugerencias, rebaten argumentos, expresan dudas, resuelven cuestiones planteadas, u ofrecen información relacionada con el tema que se trate. En este ABCdario de las Matemáticas aparecen algunas en los comentarios, y otras nos llegan a los autores mediante correos electrónicos. Todas son leídas, y algunas respondidas, si bien desearíamos disponer de más tiempo para dedicarles mayor atención. Y es realmente enriquecedor conocer e intercambiar ideas y opiniones en la mayor parte de las ocasiones. A finales de diciembre del año pasado, recibí uno de estos correos planteándome unas preguntas sobre un juego inventado por el remitente. Hoy les voy a describir dicho pasatiempo porque una vez visto con cierto detalle me parece de interés, sobre todo por el mensaje final que deseo transmitirles, y porque creo que su autor merece que se conozca su invención, y nuestro aplauso. Antes les introduzco un par de conceptos en los que se basa, que seguramente conozcan la mayoría, pero que no está de más recordar muy esquemáticamente. Cuadrados mágicosEn reseñas previas ya hemos hablado de ellos (véanse un ejemplo y otro). Un cuadrado mágico es una disposición de números en un cuadrado (pueden ser consecutivos, sólo pares, solo impares, sólo primos, repetirse o no, etc., no hay restricción, aunque los 'clásicos' son los consecutivos del 1 en adelante) de manera que todas las filas, todas las columnas, y las dos diagonales del cuadrado sumen el mismo valor (no sólo existen aditivos, sino que la operación puede ser la multiplicación también, llamándose en ese caso cuadrados mágicos multiplicativos). Se llama orden del cuadrado mágico al número de casillas que tenga cada fila (o columna).
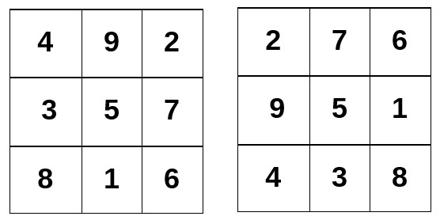
Obviamente el de orden uno es una trivialidad, de orden dos (con los números del 1 al 4) no es posible esa disposición, y la cosa empieza a ser interesante con orden tres, tratando de disponer los números del 1 al 9 cumpliendo dichas reglas. Sólo existe una disposición que lo verifica (no se cuentan giros ni simetrías; en la imagen pueden verlo en dos versiones, pero es el mismo cuadrado: en el segundo simplemente se han colocado las filas del primero como columnas, y de abajo hacia arriba), y es conocida desde el 2200 a. C., el célebre Lo-Shu chino. Con orden cuatro, es decir, disponiendo los números del 1 al 16, existen 880 configuraciones diferentes. Fue el matemático aficionado francés Bernard Frénicle de Bessy quien expuso esa cifra en la Academia de las Artes de París en 1676, y Philippe de La Hire el que hizo un listado de todos ellos en 1693. Se ha demostrado que existen 275305224 cuadrados mágicos de orden 5, pero para órdenes mayores conocer su número exacto es un problema no resuelto (por ahora sólo se tienen estimaciones aproximadas).
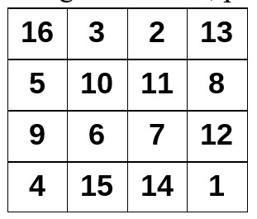
Uno de esos cuadrados mágicos, célebre por aparecer en el grabado Melancolía (1514) de Alberto Durero es el mostrado en la siguiente imagen. Además de por indicar la fecha de realización del grabado en las casillas centrales inferiores, es singular porque hay 24 configuraciones diferentes que suman 34, la constante mágica para los cuadrados de orden cuatro. Supongo que conocen porque es precisamente 34: los números del 1 al 16 suman 136, y como hay que repartirlos entre cuatro filas, cada una debe sumar 136/4 = 34. No hay ningún misterio, por mucho que queramos sacárselo al adjetivo 'mágica'. Las 24 configuraciones diferentes son las siguientes:
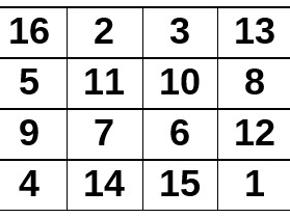
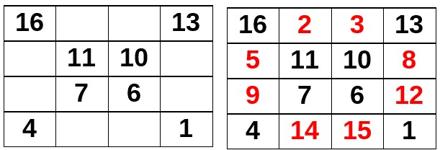
Hay alguna configuración más que suma 34, como es el movimiento del caballo de ajedrez 3 – 8 – 14 – 9 y 2 – 12 – 15 – 5. Pero nos vamos a centrar únicamente en las 24 reflejadas en la imagen anterior. Si intercambiamos las columnas segunda y tercera del cuadrado mágico, obtenemos esta otra configuración:
Es otro de los 880 posibles cuadrados mágicos de orden cuatro, que sigue cumpliendo que las 24 configuraciones de cuatro cifras descritas anteriormente suman 34. Nos quedamos con este cuadrado mágico y esas configuraciones. Desde el punto de vista matemático, los cuadrados mágicos siempre se han considerado un entretenimiento, una curiosidad sin mayor aplicación, salvo como base de algunos trucos de magia. Cuadrados latinosUn cuadrado latino (así denominado por Leonhard Euler hacia 1779 simplemente porque empleó letras latinas en su composición) es una disposición cuadrada de símbolos (pueden ser letras, números, colores, dibujos, cualquier cosa) en el que cada símbolo no se repite nunca en la misma fila o columna (matemáticamente cada fila o columna es una permutación distinta de los elementos de las otras). No hay ninguna operación aritmética (a diferencia de los cuadrados mágicos), simplemente se disponen los objetos de la manera descrita. Los sudokus son un ejemplo de cuadrado latino que utiliza los dígitos del 1 al 9.
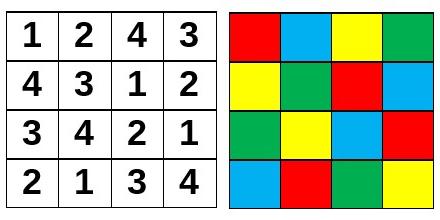
En la imagen aparece un cuadrado latino de orden cuatro con números y el mismo con colores. De orden cuatro existen 576 cuadrados latinos diferentes. Si añadimos la condición de que tampoco haya repetición en las dos diagonales (cuadrado latino diagonal), entonces hay únicamente 2 diferentes (el mostrado antes es uno de ellos, ¿podría el lector encontrar el otro?). A diferencia de los cuadrados mágicos, la teoría de cuadrados latinos constituye un campo activo de investigación matemática, al ser clave en la resolución de determinado tipo de problemas, y llevar intrínseca la estructura de grupo. Hay muchas cuestiones abiertas (planteadas y sin resolver) que involucran este tipo de cuadrados. Los FozudokusAntonio Pomares Olivares es un empleado jubilado del servicio postal británico (Post Office) que vive en Londres desde hace más de cincuenta años. Con trece años dejó de estudiar, para ponerse a trabajar, con lo que sus conocimientos matemáticos son los básicos, aunque se declara aficionado a las cuestiones de matemática recreativa, en particular de los cuadrados mágicos que le mostró su padre siendo un niño.
En uno de sus veraneos en Foz (Lugo), concretamente en 2014, jugando con unos imanes de colores, se percata de la posibilidad de colocarlos en cuatro filas sin que se repita ninguno (la estructura de un cuadrado latino que hemos comentado) y lo une al cuadrado mágico de orden cuatro descrito anteriormente formando la siguiente configuración (en la imagen, la composición que ha plasmado en la fachada de su casa gallega). Además, idea un algoritmo para generar el cuadrado a partir del orden natural de las cifras con ellas ocultas y lo escenifica como un truco de magia (no exactamente porque los magos no revelan sus métodos y Antonio sí, no tiene problema en explicarlas). En este video casero (desde el minuto 1:15), lo realiza.
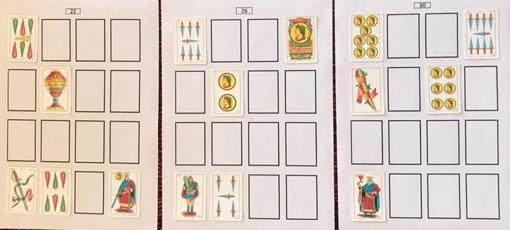
No hay duda de que dicho procedimiento es creación suya, porque en realidad la construcción de ese cuadrado es mucho más sencilla (aunque menos espectacular para hacerlo pasar como 'algo mágico', desde luego): el conocido método de la X para componer cuadrados mágicos de orden par es mucho más simple. Se trata de colocar, bien empezando desde arriba, o desde abajo, da lo mismo (lo muestro desde abajo para que quede igual que el suyo), los números naturales en su orden habitual sólo en las diagonales del cuadrado, como se ve en la imagen. Después hacemos una segunda pasada desde arriba colocando, también en su orden natural, los números que faltan (en color rojo). Así, con sólo dos pasos, construimos el cuadrado, mucho más sencillo y rápido que el procedimiento de Antonio que lo hace en tres pasos y con unos cambios bastante enrevesados. Entre los amigos a los que se lo cuenta y él mismo, deciden 'bautizar' al cuadrado con el nombre del pueblo en el que están, y lo llaman 'Cuadrado mágico de Foz'. Bien, hasta aquí, nada que no fuera conocido. La segunda parte es la interesante, y a mi juicio, novedosa (al menos yo no la he localizado en ninguna otra parte; la ha denominado Fozudoku). Traslada la idea a una baraja de cartas, en la que ahora los números son los valores de la carta, y los colores los palos (copas, espadas, oros y bastos). Normalmente utilizamos la baraja española de 40 naipes, pero él añade las necesarias para jugar al póquer, es decir, añade los ochos y nueves, con lo que tenemos 48 cartas, del 1 al 12 de cada palo. Con ellas puede construir tres cuadrados mágicos de orden cuatro. Ojo: cuadrados mágicos de cartas, no numéricos. Es decir, en cada cuadrado mágico, las filas, columnas y diagonales van a ser cartas distintas, entendiendo por distintas, de distinto valor numérico y distinto palo, porque necesariamente con cuatro ases, por ejemplo, para solo tres cuadrados, obviamente en alguno se repite el valor numérico. Es más, va a exigir, como ocurre con el cuadrado mágico de Durero y su variante, que haya otras combinaciones con la misma suma. En concreto, las mismas 24 que se indicaron arriba. Con estas condiciones, Antonio ha ideado un algoritmo de cinco pasos, en el que se pueden disponer todas las cartas de la baraja con esas condiciones, de modo que el primer cuadrado sume 22, el segundo 26 y el tercero 30. Después de colocadas todas ellas boca abajo (sin verse) mediante ese algoritmo, se descubren cinco, y a partir de ellas, se trata de intentar adivinar cuál es cada carta tapada. Un buen pasatiempo (similar al Sudoku, en el que además hay que hacer sumas) que atrae la atención de niños de primaria y personas mayores en los lugares en los que lo ha explicado (colegios, asociaciones, entre otros).
Cuestiones matemáticasInmediatamente surgen algunas cuestiones. ¿Cuántos cuadrados mágicos de este tipo se pueden construir? ¿Es obligatorio destapar cinco para resolverlos? ¿Se podría con menos? ¿Se podrían construir otras tripletas en las que la suma de los cuadrados fuera diferente? ¿Se pueden encontrar otros algoritmos que construyan Fozudokus de este tipo? Los valores numéricos que se repiten en los que ha construido (que no las cartas, volvemos a aclarar) son (1, 2, 3, 4) para el primero, (5, 6, 7, 8) para el segundo y (9, 10, 11, 12) para el tercero. ¿Podrían componerse con otras repeticiones diferentes? Antonio Pomares ha pensado también en estos y otros interrogantes. Por el momento está centrado en descubrir cuántos hay del tipo que ha ideado. Hasta el momento ha compuesto 365 posibilidades diferentes, pero no sabe si son todas las posibles o puede haber más. Recordemos que su método de trabajo, dados sus conocimientos matemáticos, es el de ensayo y descarte. Seguro que entre los lectores pueden darle alguna indicación o consejo para resolver su pregunta. Antonio también ha pensado diferentes variantes. Por ejemplo, sobre cómo utilizar esto como juego entre dos, no solo como solitario: se proponen las cinco cartas de cada uno de los tres cuadrados (quedan 33 por colocar), se reparten 10 cartas a cada jugador, quedando un mazo con 13 cartas que se colocan boca abajo encima de la mesa. Alternativamente, cada jugador coloca una carta sobre los cuadrados de acuerdo con las normas, y cuando no puede (o no sabe) colocar ninguna de las que le quedan, roba del mazo hasta que encuentre una que pueda colocar. El ganador es, obviamente, el jugador que primero termine de colocar todas sus cartas. No obstante, ha ido refinando las reglas a partir de las experiencias de personas que han practicado el juego que le han ido llegando, ya que, con un poco de práctica de ambos jugadores, esas condiciones llevan siempre a las tablas. Asimismo, ha adaptado la idea a la baraja de póquer francesa, e ideado una variante para cruces y estrellas mágicas. Y ha desarrollado un caso aún más complejo en el que los Fozudokus deben verificar 36 combinaciones distintas, en lugar de las 24 mencionadas. Lo ha denominado 'Fozudoku del muro', y la solución parece ser única. Toda la información, detalles, videos ejemplo, ficheros con todas las posibilidades, absolutamente todo lo que ha ido deduciendo lo comparte en varios idiomas en este enlace. Para terminarEs evidente que juegos como éste son un buen ejercicio, tanto para niños como para adultos, ayudando a desarrollar y mantener nuestra agilidad mental. Pero, sobre todo, ha sido, y es, un reto personal para el propio Antonio, un aliciente con el que ocupar y disfrutar de las horas del día, aportando además algo provechoso para todo el mundo. Las matemáticas (también otras disciplinas, como la literatura, la historia, la pintura, la música, en realidad cualquier actividad humana) permiten a las personas investigar, aprender y compartir conocimiento. La diferencia es que algunas requieren más esfuerzo o aptitudes específicas (leer mucho, redactar bien, tener buen oído, etc.) y paradójicamente, a pesar de ser considerada una disciplina compleja, las matemáticas tienen muchos niveles de profundización, y como vemos, con poquita cosa, con contenidos muy sencillos, podemos adentrarnos, con ingenio y perseverancia, en asuntos apasionantes y relevantes incluso. Con los Fozudokus, además de actividades en algunos centros educativos de Foz, de Alicante (la ciudad natal de Antonio; por ejemplo, en la Asociación de Vecinos El Templete de Benalúa), de Londres (incluyendo un centro de sordomudos), este pasatiempo ha sido utilizado en el 'Festival Matemático Julia Robinson', un crucero virtual por 22 países de Iberoamérica en que se trabajaron diferentes aspectos de las matemáticas a partir de juegos, celebrado el pasado mes de abril. Gracias a la colaboración de amigos, vecinos y otras personas, esta iniciativa se va abriendo camino, a través de las redes, de los medios de comunicación, etc. ¡¡Que cunda el ejemplo!! Alfonso J. Población Sáez es profesor de la Universidad de Valladolid y miembro de la Comisión de divulgación de la RSME. El ABCDARIO DE LAS MATEMÁTICAS es una sección que surge de la colaboración con la Comisión de Divulgación de la Real Sociedad Matemática Española (RSME) |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |