El profesor de matemáticas bilbaíno que hacía bailar a los números
El profesor de matemáticas bilbaíno que hacía bailar a los números |
 |
 |
 |
|
ABC, 14 de Junio de 2021 El autor recuerda a Héctor Antoñana, autor de un ingenioso libro de matemáticas en los años 80
Adobe Stock
Recordarán los lectores más fieles que hace unos meses esbocé una semblanza de Mariano Mataix, centrándome sobre todo en su faceta de escritor de libros de matemática recreativa, al ser, junto a Martin Gardner, uno de los autores que más leí en mi etapa de estudiante. Asimismo, les anunciaba mi intención de dedicar de vez en cuando estas breves líneas a evocar aquellos textos que, aunque no tuvieran tanto alcance como los que nos venían de fuera, también merecen su espacio y seguramente tuvieron su influencia en que algunos orientáramos nuestra carrera profesional en la enseñanza y/o divulgación de las matemáticas. Creo que es justo, por tanto, reconocer su mérito, fuera poco o mucho, y que no queden olvidados para siempre. Además, puede que, en algún momento, caiga en nuestras manos alguno de sus libros, de una biblioteca, de una librería de lance, de la desmantelada vivienda de algún familiar, y queramos saber algo de sus autores.
Hacia el año 1983, justo antes de comenzar mis estudios en la facultad, en ese verano antesala de comenzar la Universidad, una vez hecha la Selectividad de entonces y habiendo pagado ya la matrícula del curso, con ese run-run con el que todo el mundo te machacaba de “no sabes dónde te metes”, “¿matemáticas? pero si acaban todos locos”, etc., etc. (espero que ya no se diga eso, y que estas reseñas hayan contribuido a cambiar esa leyenda urbana; de hecho, así debe ser, porque ahora se pide una nota altísima para acceder a esos estudios), cayeron en mis manos algunos libros de matemática recreativa. Padres, profesores, compañeros mayores, te sugerían que fueras leyendo (incluso repasando) los límites, las derivadas, las integrales… Pero, obviamente, con el calor no apetecía demasiado empezar lo que sería irremediable tres meses después. Los acertijos, los juegos, los problemas de lógica, las anécdotas de la vida de los matemáticos eran mucho más deseables. Y en ese verano me prestaron dos: 'Nuevos pasatiempos matemáticos', de Martin Gardner (publicado por Alianza Editorial) y 'La danza de los números', de un tal Héctor Antoñana, cuya portada ven en la imagen adjunta. De este autor es del que quiero hablar hoy. Ambos son libros de bolsillo, absurdo intentar fotocopiarlos, por tanto. Los leí de cabo a rabo en poco tiempo, y me llamaron la atención muchas cosas, completamente desconocidas para mí. Así que, me puse a copiar lo que me interesaba, con mis propias anotaciones entremedias, o añadidos que veía en otros libros o revistas. Conservo esos folios. Los de Gardner podía haberlos tirado a la basura porque con el tiempo he ido comprando todos los libros que han ido presentándose a mi alcance. Pero no así el segundo. No encontré por ninguna parte ningún dato del señor Antoñana (pensemos que aún no existía internet en los ochenta, al menos para la gente común). Pensé que sería algún autor anónimo de los que de vez en cuando recopilan ejercicios de aquí y de allá, y tiene la suerte o el contacto adecuado para que le publiquen un libro. Pero después de publicar en esta sección el recuerdo de Mataix, me acordé de aquel libro y aquel nombre. Y encontré algunos datos, que paso a resumirles. Es triste en la condición humana el que nadie te haga caso nunca en vida y se acuerden de ti criando malvas, pero lo cierto es que, en las necrológicas, en las esquelas, es uno de los lugares en los que más información acabas encontrando de muchas personas. Y tal es el caso. Héctor Antoñana Gortázar nace en Bilbao el 3 de agosto de 1922, cerca de la Gran Vía. Sobre su vida no he encontrado demasiados detalles, fuera de su trabajo como religioso: estudia en el Colegio Santiago Apóstol, de los hermanos de La Salle, en Bilbao; ingresa en la Compañía de Jesús, desarrollándose toda su trayectoria profesional en centros e instituciones de la Compañía, la mayor parte en el colegio San José de Durango (Vizcaya), donde desempeña diferentes cargos, entre los que estuvo el de profesor de dibujo y matemáticas entre 1962 y 1994. Según los testimonios de personas que lo conocieron personalmente, fue una persona con un especial sentido del humor, al que nunca faltaba la frase ingeniosa o el chiste, no sólo como diversión sino también como reflexión. En lo que nos atañe aquí, sus alumnos indican que hacía vivir las matemáticas mediante ejemplos, trucos, cuestiones de ingenio, provocando la curiosidad. Buscaba recursos en los lugares más inverosímiles, y era cercano al estudiante, que estaba encantado con estas excursiones fuera del tradicional libro de texto. Cuentan que su cabeza iba más rápido que sus explicaciones, lo que muchas veces complicaba ser entendido oralmente, pero ese inconveniente era suplido con sus ejemplos y demostraciones. Escribió varios libros (doctrinales básicamente, salvo uno de filatelia vasca, en colaboración con sus alumnos), y sólo uno, el citado anteriormente, relacionado con las matemáticas. Hizo también algunas traducciones al español de textos franceses. Falleció en Madrid el 9 de noviembre de 2016, a los 94 años de edad.
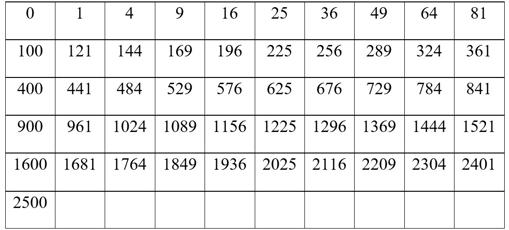
'La danza de los números'El libro está estructurado en dos partes claramente diferenciadas, cada una con varios capítulos. La primera de esas partes se dedica a recopilar diferentes temas relacionados con los números, mientras que la segunda son ejercicios concretos resueltos y comentados. En el primer capítulo, 'Números curiosos', Antoñana nos muestra algunas de las más conocidas (algunas no tanto) curiosidades y 'casualidades' numéricas (el entrecomillado es, obviamente, porque ya saben que en matemáticas no existen casualidades), algunas también descritas en esta serie de artículos (véase éste, por ejemplo). El lenguaje en que escribe el libro es coloquial, como si nos estuviera hablando de tú a tú. Una muestra: Un problema que propuse a un alumno y no me supo resolver es, ya metidos en cálculos, buscar y hallar el número que, multiplicado por 49, nos dé otra vez todos 1. La solución, y perdona la broma es 2.267.573.696.145.124.716.553.287.981.859.410.430.839 Recordemos que el libro está publicado en 1982, y los ordenadores personales no estaban aún generalizados. Las calculadoras no nos dan más de ocho cifras, de modo que, o directamente encontró ese número en algún artículo o libro, o lo dedujo él mismo. Como no aporta bibliografía, no lo sabremos nunca. Otra “llamativa” relación que describe es con las terminaciones de las potencias sucesivas de los números naturales. Por ejemplo, con los cuadrados:
Reproduzco nuevamente sus propias palabras: “… basta fijarse en las terminaciones para quedar sorprendido ante el resultado: 0 – 1 – 4 – 9 – 6 – 5 – 6 – 9 – 4 – 1 – 0. Un perfecto capicúa. Más aún. Tomando las terminaciones de dos en dos cifras, se forma un periodo de 51 dígitos: 00 – 01 – 04 – 09 – 16 – …. – 16 – 09 – 04 – 01 – 00. Y estas consideraciones pueden extenderse indefinidamente. Así, las tres últimas cifras de los cuadrados consecutivos forman un periodo de 501 cifras. Y las cuatro últimas constituyen un periodo que se repite cada 2501 cifras, y así sucesivamente. Pero basta ya de casualidades”. Evidentemente es un buen anzuelo para que el lector piense ¿Y por qué pasa esto?, y se ponga a intentar ver la razón (si alguno lo hace, ya sabe, congruencias). En el segundo capítulo, 'Rarezas que no son rarezas', es un listado de propiedades numéricas, pero ahora sí, hace con detalle las demostraciones. Son enunciados sencillos, pero ilustrativos para que el lector no versado en matemáticas, se 'entrene' y conozca la filosofía de las demostraciones matemáticas. Por ejemplo (inténtenlo; es muy sencillo): “Todo número primo aumentado o disminuido en una unidad es siempre múltiplo de 6”. El tercer capítulo nos presenta los 'Números perfectos', los siguientes van dedicados a los 'Números amigos', 'Pitágoras sin triángulo', 'Con cifras iguales' (expresar los números con un número determinado de cifras iguales; por ejemplo, con tres nueves, tres cuatros, etc.), 'Con cuatro cifras' (sobre escribir el mayor número posible con sólo cuatro cifras), 'El calculador relámpago' (sobre calculadores prodigio y algunos de sus trucos; recientemente ha aparecido un libro dedicado exclusivamente a este tema, 'Calculadoras humanas', de Vicente Meavilla; con esto quiero indicar que todos estos temas no han perdido actualidad, y periódicamente siguen aportándose nuevos datos, con nuevas metodologías y nuevos puntos de vista), 'Persistencia', '¿Casualidades?', 'Cuadrados mágicos', 'Cuadrados Latinos' (seguro que estos dos capítulos les suenan, aunque nada de lo que aparece lo tomé para mis anteriores reseñas), 'El sistema binario', 'Álgebra Aplicada' y 'Matemáticas Modulares'. En este último capítulo, aparece una respuesta ingeniosa (humorística, más bien) al famoso problema de los granos de trigo que la leyenda dice que pidió el inventor de ajedrez como recompensa a su invención, que como saben es 264 - 1 = 18446744073709551615Antoñana indica que una posible respuesta del rey al inventor, si hubiera sabido algo de matemáticas es haberle dado 3 granos de trigo, porque 264 - 1 ≡ 3 (mod 7)Como ven, humor no le faltaba al autor, aunque me parece que hizo mal la cuenta, o hay una errata, porque esto es falso. Si quiere que sea congruente con 7, debería darle 8 granos de trigo, no 3. Pero ya puestos, dado que el damero habitual es 8 x 8, yo usaría módulo 8, y entonces le daría 7 granos de trigo, quedando así números más 'bonitos' (ya saben que todo lo que entrecomillo va con retintín). La segunda parte del libro la dedica a plantear y resolver ejercicios curiosos, como ya comenté anteriormente. Empieza con algunos relacionados históricamente con grandes sabios (Arquímedes y su Eureka, a su uso de la palanca, al célebre arbelos, o a su epitafio en el que aparecen cono, cilindro y esfera y la relación entre sus áreas y volúmenes; el reloj de Einstein; al epitafio de Diofanto; a la lúnula de Hipócrates; A Euclides, etc.), para luego hacer una recopilación de problemas en diferentes contextos, perfectamente clasificados (colecciones clásicas, cuestiones de proporcionalidad, cálculo de probabilidades, observando la Naturaleza, etc.). A los matemáticos actuales no suelen gustarnos esta filosofía “antigua” de mostrar las materias a base de colecciones y listados de ejercicios y/o chascarrillos (aunque siguen editándose), porque preferimos una visión no tan puntual sino más didáctica, más estructurada. Pero como digo, siguen teniendo su público. Muchas de las cuestiones planteadas en este libro aparecen en otros textos periódicamente. Lo que hace distinto éste en particular es su peculiar manera de comentarlas y resolverlas. No obstante, no deja de ser llamativo que, habiendo escrito un único libro sobre este tema (probablemente vean en internet que también publicó uno titulado 'Curiosidades Matemáticas: no hay tal'. Observen que en realidad es el subtítulo del de 'La danza de los números'), esté referenciado por muchos autores. No es que tuviera una tirada enorme (y mucho menos tratándose de una editorial de publicaciones religiosas en su mayoría); es sencillamente que, en España, fuera de los libros de texto convencionales, se editaban muy pocos libros que tuvieran nada que ver con las matemáticas (a diferencia de lo que sucedía en otros países). Por tanto, como conclusión final les diría que nunca desdeñen un libro (o una película) por su antigüedad, su apariencia, su autor o porque aparezca en el trastero del abuelo. Siempre habrá algo útil y aprovechable en él (además de hacer revivir en cierto modo a la persona que lo concibió). Alfonso J. Población Sáez es profesor de la Universidad de Valladolid y miembro de la Comisión de divulgación de la RSME. El ABCDARIO DE LAS MATEMÁTICAS es una sección que surge de la colaboración con la Comisión de Divulgación de la Real Sociedad Matemática Española (RSME) |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |