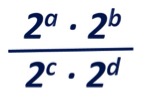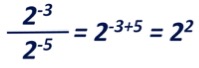Septiembre 2021: Matemáticas con una baraja corriente (III)
Septiembre 2021: Matemáticas con una baraja corriente (III) |
 |
 |
 |
| Escrito por José Muñoz Santonja |
| Miércoles 01 de Septiembre de 2021 |
|
Entramos en la última entrega, al menos de momento, de los juegos de cartas para practicar cálculo aritmético, utilizando una baraja de las usadas fuera de la escuela para los juegos sociales. En general son propuestas de juegos para Secundaria, bien primer o segundo ciclo. En esta ocasión vamos a comenzar a trabajar con fracciones y las operaciones aritméticas que no son las básicas y que se trabajan en este bloque. 1. La fracción como operador.Es un juego para varios jugadores, hasta seis. Se utiliza una baraja con los valores del 1 al 9. Antes de empezar se fija un número de tres cifras que será el valor base, por ejemplo, 420. El número lo pueden decidir entre los jugadores o ser el profesor el que indique el número con el que trabajar. Tras barajar el mazo de cartas se entregan cuatro cartas a cada jugador. Cada jugador debe construir una fracción con dos de sus cartas, que se multiplicará por el valor base fijado, y se hallará cuánto vale la fracción de esa cantidad. Es obligatorio que el resultado de la operación sea un número entero. Todo jugador que escriba una fracción correcta, sea propia o impropia, que al multiplicarla por 420, o el valor que se decida, dé un número entero, se anota un punto. También se anota un punto más el que haya obtenido el menor valor resultante de la operación, y dos puntos más el que obtenga el mayor valor resultante. Las cartas que se han usado para formar las fracciones se descartan en un mazo aparte. Si algún jugador no ha podido formar una fracción con la que multiplicar el valor base para obtener un entero, puede descartarse de dos de las cartas que tiene, las que él prefiera. Del mazo original se entregan dos cartas más a cada jugador, de forma que vuelvan a tener cuatro cartas. Y se vuelve a repetir el proceso. Se continúa el juego hasta que ya no quedan cartas en el mazo. Entonces se cuentan los puntos conseguidos y gana el jugador con más puntos. Hay una alternativa a este juego, aunque de forma similar. En esta modalidad se deben tener una serie de tarjetas con números de tres cifras que serán los valores sobre los que operen las fracciones. Se reparten todas las cartas entre los jugadores y se coloca el montón de tarjetas con números boca abajo sobre la mesa. En cada jugada, se extrae una carta del mazo de valores y los jugadores deben construir, con dos de sus cartas, una fracción que multiplicar por ese valor, obteniendo un número entero. Igual que en el caso anterior, todo el que pueda construir una fracción que al multiplicarla por el número fijado dé un entero, se anota un punto. Quien obtenga el mayor resultado entero dos puntos extras, y uno para el que consiga la menor fracción. Una vez realizado el cálculo, se descarta el número utilizado y las cartas que se hayan usado. Se continúa el juego sacando otro número del mazo de valores y repitiendo el proceso mientras queden cartas en la mano de los jugadores, o números en el mazo de valores. Como las cartas que se usan se van descartando, a la larga el juego se convierte en un juego de estrategia, pues hay que intentar quedarse con cartas que nos permitan hacer varias fracciones para operar con los números de tres cifras. En el juego está implícito, aunque no se especifique, el trabajo con múltiplos y divisores, pues debemos construir siempre una fracción que, simplificada, tenga un denominador que sea divisor del valor con el que operar. El mazo de valores por el que multiplicar puede proporcionarlo el profesor, aunque es más provechoso que cada alumno proponga uno o varios números de tres cifras para jugar. De esta manera aparecen los problemas con números escritos aleatoriamente y que pueden tener pocos divisores o hasta ser primos, con lo que sólo se pueden multiplicar por fracciones equivalentes a un número entero. Al principio se planteó que se jugaran sólo con las cartas del 1 al 9. Se puede ampliar, si se quiere, a toda la baraja, tanto española como francesa. La cuestión es que es más difícil que las cartas 11 y/o 13 se puedan utilizar como denominador en una fracción como se busca. 2. Fracciones equivalentes.Se juega con la baraja completa española de 48 cartas, o en su defecto con la francesa. Pueden jugar hasta cuatro jugadores. Se barajan las cartas y se colocan a la vista sobre la mesa seis de ellas, y se entregan cinco cartas a cada jugador. Comenzando por el de la derecha que ha repartido, cada jugador en su turno comprueba si puede hacer una fracción con sus cartas, y otra con las cartas que están sobre la mesa de forma que sean fracciones equivalentes. Si lo logra recoge las cuartas cartas y las acumula en un montón personal de descartes. A continuación toma del mazo dos cartas para las que tiene en la mano y repone dos cartas sobre la mesa, quedando la distribución como estaba antes de jugar. Entonces pasa el turno al siguiente jugador. Si no logra formar fracciones equivalentes, pasa el turno. El juego se continúa mientras queden cartas en el mazo. Cada jugador se anota dos puntos cada vez que consigue formar dos fracciones equivalentes. Basta sumar las cartas del montón de descartes y dividir entre dos. Como es usual, gana el jugador que ha conseguido más puntos. 3. La fracción más cercana.En el artículo anterior hablé de la página de Denise Garkins en la que existían muchos juegos a realizar con cartas corrientes. En su caso siempre se proponen con cartas de póker. En esa página encontré hace tiempo el siguiente juegoi. Juegan dos o tres jugadores, aunque en el artículo original si juegan tres o cuatro jugadores se necesitarían dos barajas, pero no lo creo necesario. Se reparten cinco cartas a cada jugador y se plantean una serie de retos independientes. En cada jugada, el jugador debe encontrar, entre sus cartas, dos que formen una fracción que sea lo más cercana posible al reto propuesto. Los retos los fija el profesor antes de comenzar a jugar y puede variarlos según los grupos o el nivel de conocimientos del alumnado. Ejemplo de retos son los siguientes:
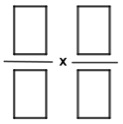
En cada ronda se propone un reto y todos los jugadores muestran una fracción, el jugador que se acerca más al valor pedido se lleva todas las cartas que se han utilizado para proponer las fracciones. A continuación, se reponen las dos cartas utilizadas a cada jugador y se pasa a la siguiente ronda. Se continúa mientras queden retos o cartas en el mazo. Al final gana quien ha recogido más cartas. Tal como está planteado hasta el momento, tiene relación con el juego anterior, ya que bastaría en cada caso presentar una fracción equivalente al valor buscado, salvo en el cero, pero en la página de Denise Gaskins se impone que la fracción no puede ser equivalente o igual al valor propuesto, es decir, se obliga a que se busque una fracción distinta, pero lo más cercana posible al reto. Los retos pueden estar prefijados desde el principio o irse construyendo a medida que se hace el juego. Por ejemplo, se lanzan dos dados y el primero sería el numerador y el segundo el denominador de una fracción que es a la que se debe acercar. Otra posibilidad es que uno de los jugadores que no haya ganado hasta el momento, sea quien proponga la fracción a conseguir en la siguiente ronda. Aunque el que proponga tenga una fracción cercana, no puede saber si algún otro jugador puede construir otra que sea aún más cercana. 4. Operaciones con fracciones.Este juegoii lo encontré en la página de Ana García Azcárate. Se juega con una baraja francesa sin las figuras. Se barajan las cartas y se coloca el mazo, boca abajo, en el centro de la mesa. También se coloca un tablero como el de la siguiente imagen.
Imagen 1: Tablero para el producto de fracciones. Es un juego para dos o cuatro jugadores. Cada jugador en su turno, que comienza por el que ha barajado el mazo y en sentido antihorario, toma una carta del mazo y la coloca en una casilla del tablero. Cuando ya se han colocado las cuatro cartas, cada jugador debe hallar el resultado de multiplicar las dos fracciones. Todo jugador que dé correcto el resultado se anota cinco puntos. Si además la fracción está totalmente simplificada, siempre que sea posible, se anota cinco puntos más. Se separan las cartas que se han utilizado en esa operación y se vuelve a repetir el proceso tomando cuatro cartas del mazo colocadas sobre el tablero. Cuando se han acabado las cartas, es decir, después de nueve jugadas, gana quien haya acumulado más puntos. La versión que propone Ana es un poco diferente. En esa opción cada jugador tiene delante un tablero como el de la imagen 1 y trabaja con sus propias fracciones. Comienza el jugador a la derecha del que ha barajado, toma una carta del mazo y la coloca en su tablero, el jugador a su derecha toma otra carta y la coloca en su tablero, y así sucesivamente hasta que todos los jugadores han colocado cuatro cartas en su tablero. En ese momento los jugadores deben hacer el cálculo y expresar el resultado simplificado del producto de sus fracciones. La puntuación es la misma que en el caso anterior, pero se pueden dar puntos extras, por ejemplo 3 puntos, al jugador que ha obtenido la mayor fracción y otros tres al que ha obtenido menor fracción. El juego termina después del número de jugadas que se haya estipulado al principio, por ejemplo diez. En esta versión pueden jugar también tres o cinco jugadores, no es conveniente grupos de más de cinco jugadores. Al acabar cada jugada, se recogen todas las cartas y el jugador a la derecha del que antes había barajado, es el que se encarga ahora de barajar el mazo. Como es evidente, la operación a realizar se puede modificar según lo que se quiera practicar. Es decir podemos trabajar la división de las dos fracciones, pero también la suma o la resta. Incluso se puede hacer de forma aleatoria. El mismo jugador que, en cada jugada, mezcla las cartas del mazo lanza un dado. Si sale 1 hay que realizar la suma, si sale un 2 la resta, con el 3 multiplicamos y para el 4 dejamos la división. Si el dado es de seis caras cuando sale un 5 o un 6 se vuelve a tirar. 5. Operaciones con potencias.Esta es una adaptación de un juegoiii propuesto por Ana García Azcárate para repasar el producto y cociente de potencias. Es un juego para varios jugadores y se trabaja con una baraja francesa sin figuras en la que las cartas rojas equivalen a números negativos y las negras a positivos. Se barajan las cartas del mazo y se colocan boca abajo sobre la mesa. El mismo jugador que ha barajado extrae cuatro cartas del mazo y las muestra en la mesa. Los valores obtenidos en las cuatro cartas serán los exponentes de cuatro potencias que corresponderán a la siguiente expresión. Es decir, a, b c y d son los valores que se han obtenido en las cartas.
Imagen 2: Operación con potencias. Los jugadores pueden colocar en cada exponente el valor que quieran de los extraídos en las cartas, y después tienen que reducir la expresión a una sola potencia de exponente 2. Todo jugador que realiza correctamente la operación se anota cinco puntos. El que obtiene la mayor potencia se adjudica cinco puntos más, y otros cinco el que obtiene el menos valor, siempre que jueguen más de tres jugadores. Las cartas extraídas se desechan y se extraen otras cuatro, volviéndose a repetir el proceso. Después de cinco tandas gana el jugador que tenga más puntuación. Este juego permite simplificar o complicar el desarrollo según el nivel donde queramos trabajar estos contenidos. Tal como lo plantea Ana García en su propuesta, cada jugador saca dos cartas, la primera es el exponente del primer operador y el segundo el del siguiente operador. Se extrae también una tarjeta con operaciones, bien de multiplicación o división. Entonces el jugador opera 2carta1 con 2carta2 según la operación que haya obtenido. Anota la operación y el resultado en su cuaderno. Por ejemplo, ha obtenido en la primera carta un -3 y en la segunda un -5 y la operación de división. Debe hacer la operación:
Imagen 3: Ejemplo de cálculo. Al final, cuando todos los restantes jugadores hagan lo mismo, extrayendo cada uno sus cartas y su operación, gana el que ha obtenido una potencia mayor. Ese jugador se lleva todas las cartas que se han utilizado en esa mano. Se repite el proceso, al menos cinco veces, y gana el jugador que al final tiene más cartas. En su artículo, Ana García propone utilizar un conjunto de 12 tarjetas, seis con la operación producto y otras seis con la división. Yo prefiero utilizar una moneda o un dado y cada jugador, tras extraer las dos cartas lo lanza y si obtiene cara o par, debe hacer un producto y si obtiene cruz o impar debe dividir las dos potencias. Para no aprovechar directamente el cálculo hecho por otro compañero en una ronda anterior, se pueden ir cambiando las bases de las potencias en cada jugada. Bien siguiendo un patrón o echando un dado y tomando el valor obtenido salvo el 1. Es posible que algún jugador observe la tónica del cálculo indistintamente de cuál sea la base, pero eso es señal de que ha aprendido como debe realizar el cálculo. En la forma anterior de jugar se repasan los productos y divisiones de potencias de la misma base. Para añadir también el repaso de la potencia de la potencia, se pueden presentar el producto de potencias de distinta base no siendo esas bases números primos. Por ejemplo, jugando como hemos visto en la primera versión que he propuesto del juego, podríamos sacar tres cartas y realizar la operación de la imagen 4, con la exigencia de que el resultado debe ser una potencia de base un número primo.
Imagen 4: Potencias de base un número no necesariamente primo. Y ya puestos a complicar el cálculo se pueden utilizar números que haya que descomponer previamente, por ejemplo, extraer dos cartas de valores a y b y efectuar el producto o división de 12a · 18b. Dando el resultado como producto de dos potencias de base un número primo. 6. Potencias y raíces.Antes hemos repasado el cálculo con potencias, pero se puede jugar repasando los valores aproximados de potencias y raíces con el siguiente juego. Vamos a jugar con una baraja de cartas sin figuras, sólo las cartas del 1 al 9. Y necesitaremos un dado cúbico. Pueden jugar varios jugadores, por ejemplo cuatro. Se barajan las cartas y se entregan cinco a cada jugador. Se lanza el dado y se obtiene un valor que será 4, 5 ó 6, y en el caso de salir un 1 se considerará un siete, en el 2 se considerará un ocho y en el 3 un nueve. También se puede extraer una carta de la baraja y mostrarla, siempre que sea mayor que 3. Cada jugador debe elegir dos de sus cartas y construir un número de dos cifras que sea el cuadrado del valor obtenido. Todo jugador que lo consiga se anota tres puntos. Si nadie lo logra se anotará dos puntos el jugador cuyo número construido sea lo más cercano al cuadrado buscado, lo sea tanto por exceso como por defecto. Se descartan las cartas que se han utilizado y se reparten dos a cada jugador para reponer las usadas en la mano anterior. Cuando se acaban las cartas del mazo (antes del último reparto se muestra la carta que fijará el valor que hay que hallar al cuadrado), se acaba el juego y gana el jugador que haya conseguido más puntos. De forma similar se puede jugar a la operación inversa. Si juegan dos o tres jugadores se reparten ocho cartas a cada jugador, si son cuatro se reparten seis. Las cartas que quedan en el mazo se barajan y se extraen dos de ellas con las que se forma el número de dos cifras más grande posible. Cada jugador echa sobre la mesa una carta que sea la raíz cuadrada más cercana al número que se ha construido. Para que no haya copias en el proceso, cada jugador coloca frente a él y boca abajo sobre la mesa, la carta que cree que es la raíz cuadrada más cercana. Una vez que están todas colocadas se les da la vuelta y se comprueba la solución. Todos aquellos cuyo valor sea el más cercano a la raíz cuadrada del número obtenido en el mazo, se anota tres puntos. Tras ello se descartan tanto las cartas que se han puesto sobre la mesa como las que se han sacado del mazo. Se repite el proceso extrayendo otras dos cartas del mazo y volviendo a construir un número de dos cifras y buscando, cada jugador, entre las cartas que le queden en la mano, la más cercana a la raíz cuadrada. Se continúa el juego hasta que se han realizado cinco rondas en cuyo caso termina la partida, y gana el jugador que haya acumulado más puntos. No es raro que haya varios jugadores con la misma puntuación, entonces todos ellos son los ganadores. 7. Y hasta aquí ha dado de sí.En estos tres artículos encadenados hemos pretendido mostrar una serie de juegos que se pueden jugar en el aula, utilizando barajas corrientes que suelen ser fáciles de conseguir, para que el profesor no tenga que entretenerse en construir material para una clase completa o comprar barajas especiales que suelen sobrepasar las capacidades económicas de los departamentos. Muchos de los juegos son similares o se basan en principios y dinámicas muy similares, pero el objetivo no es usar todos los juegos el mismo curso ni con los mismos alumnos. Es verdad que al alumnado suele resultarle atractivo el jugar con las cartas y muchas veces no reconocen que les estamos proponiendo una serie de ejercicios, que si estuviesen escritos en una página quizás ni siquiera los mirarían dos veces, pero también he reconocido en varias ocasiones que los recursos que se utilicen en clase deben ser variados para no perder efectividad al convertirse en rutinarios. Debemos alternar comentarios y lecturas de textos matemáticos, geometría dinámica, audiovisuales, material manipulable, juegos, puzles, etc… Por ello, esta colección de juegos que he presentado es un banco de recursos para que cada profesor seleccione cuál cree que le conviene más al alumnado que tiene en su aula y, igual que he hecho yo en muchos de ellos, lo adapten a su situación concreta. Si les sirve para que las clases sean más atractivas y hagan que el alumnado trabaje con más ganas y en mejores situaciones, habrá merecido la pena el trabajo dedicado a su escritura.
Notas:[i] https://denisegaskins.com/2014/08/06/fraction-game-my-closest-neighbor/ [ii] https://anagarciaazcarate.wordpress.com/2017/11/07/cartas-multiplicar-y-dividir-fracciones/ [iii] https://anagarciaazcarate.wordpress.com/2019/06/11/cartas-para-las-operaciones-con-potencias/ |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |