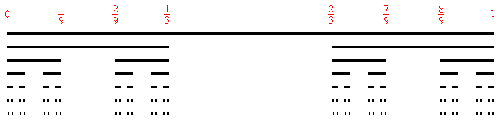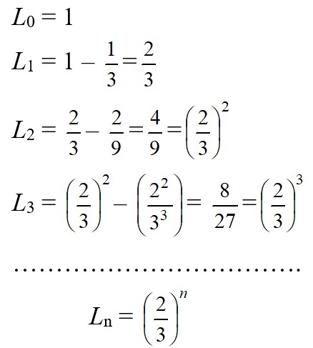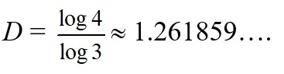Fractales: las formas que simulan a la naturaleza
Fractales: las formas que simulan a la naturaleza |
 |
 |
 |
|
ABC, 22 de Noviembre de 2021
Observando esta imagen quizá pensemos que se ha tomado con un dron y una cámara de alta resolución o algo similar. En realidad, no existe: es una imagen fractal creada gracias a unas funciones matemáticas y un procedimiento repetitivo simulado con un ordenador
Un paisaje fractal creado por ordenador - Wikicommons Seguramente alguna vez hayamos oído comentar aquello de Existen otros mundos, pero están en éste, del poeta surrealista francés Paul Éluard (que, por cierto, se llamaba en realidad Eugène Émile Paul Grindel), frase muy utilizada en anuncios publicitarios, programas de televisión, guiones de películas, seguramente por el tono romántico de misterio (en realidad, de no-misterio) que sugiere. En esta ocasión, voy a tratar de “convencerles” de que, algunos objetos y propiedades matemáticas, se ajustan perfectamente a la frase. Estamos atrapados en un mundo tridimensional (aunque algunos se empeñen en pensar que es plano, como su encefalograma; mejor dicho, ese no es plano, es unidimensional, una línea recta). Las tres dimensiones son largo, alto y ancho, que matemáticamente se representan mediante un sistema de tres ejes perpendiculares: x, y, z.
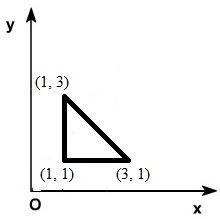
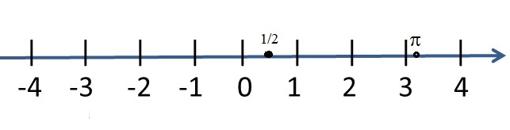
Del mismo modo, si sólo utilizamos dos ejes, el OX y el OY, la dimensión sería 2, y los objetos que podemos contemplar en ese caso son planos. Por ejemplo, el triángulo rectángulo de la segunda imagen, es plano, sólo tiene largo (la longitud a lo largo del eje OX) y ancho (la longitud a lo largo del eje OY), y cada vértice puede designarse por dos coordenadas. Uniendo después esos vértices tenemos el triángulo. Su dimensión es 2. Finalmente, si no se considera más que una dirección (un solo eje), nuestro universo sería una recta, y sus 'habitantes' son puntos, que están todos colocaditos a lo largo de esa recta. En la imagen aparecen señalados el ½ y el número π. Esa recta tiene dimensión 1, pero ¡¡cuidado!!, cada uno de los puntos que la conforman (el 2, el π, el 200) tiene dimensión 0. El asunto que provoca que separadamente no tengan dimensión (es obvio, ni tienen largo, ni ancho, ni nada) y al ponerlos todos juntos en la recta real pasen a dimensión 1 es claro: hay infinitos, llenan completamente todos los huecos de la recta, no hay sitio para más (los matemáticos decimos, tras unas definiciones y pruebas rigurosas y consistentes que forman un conjunto denso).
Por tanto, a modo de resumen, tenemos puntos (con dimensión nula), rectas (con dimensión 1; solo una dirección), superficies planas (con dimensión 2; dos direcciones perpendiculares, una mide el largo y otra el ancho) y superficies tridimensionales (con dimensión 3; tres direcciones perpendiculares, una para el largo, otra para el ancho y la última para lo alto). ¿Y si les digo que existen a nuestro alrededor “entes” con una dimensión fraccionaria, no entera, 2/3, por ejemplo? No, no es ciencia ficción, son matemáticas, y serias. Pasen y vean. Si empezamos por el principio, vayamos al año 1883. El matemático Georg Cantor (uno de los más importantes de la historia; trabajó en la formalización del concepto de infinito, en tratar de entender las numerosas paradojas que a lo largo del tiempo fueron surgiendo en torno a ese concepto, lo que le llevó a desarrollar la teoría de conjuntos, entre otros valiosos hallazgos), introduce la siguiente construcción gráfica: partamos del intervalo cerrado [0, 1]. Dividimos ese intervalo en tres partes iguales, y eliminamos el tercio central. Esa misma operación la realizamos indefinidamente en cada uno de los trozos que nos van quedando, quedando en las primeras seis etapas (iteraciones, se llaman técnicamente) como vemos en la imagen:
El conjunto de Cantor sería el resultado final cuando iteramos este proceso hasta infinito, es decir, la unión de todos los puntos que sobreviven al proceso anterior. Algún escéptico pensará, con toda la razón, si al final queda algún punto. Ese es el primer paso que debe hacerse en matemáticas cuando se define o se realiza una construcción un tanto “exótica” como ésta: probar que el conjunto resultante no está vacío, que contiene algún elemento. De la propia construcción, se observa que todos los extremos de los intervalos que van quedando, van a estar siempre. Es decir, el punto 0 y el 1, 1/3 y 2/3, 1/9, 2/9, 7/9 y 8/9, etc. Por tanto, es un conjunto no vacío, y además infinito (se puede construir una función desde este conjunto al intervalo [0, 1] que demuestra que ambos tienen el mismo cardinal, es decir, el mismo número de elementos; y como sabemos el [0, 1] tiene infinitos puntos). Es un conjunto que no tiene dimensión 1 (no es una recta, tiene muchos “agujeros”), pero tampoco tiene dimensión 0 (ya que contiene infinitos puntos). Su dimensión, en buena lógica, debería ser un valor entre 0 y 1. Para este tipo de construcciones se han definido varias generalizaciones al concepto de dimensión, que coinciden para objetos “corrientes” (es decir, los valores enteros indicados antes para puntos, rectas, superficies planas y cuerpos tridimensionales), pero que además permiten asignar una dimensión fraccionaria a estos otros objetos. Una de ellas es la dimensión fractal, idónea para construcciones del estilo de la anterior, en la que se eliminan o añaden sucesivamente trozos en infinitas etapas. Los objetos resultantes se llaman fractales (proviene del término fractus, que significa quebrado), y al final indico porqué surgen, y lo que son. Antes terminemos con este ejemplo. Dimensión fractalUna de las características que se observan de este tipo de construcciones sin más que mirarlas, es la autosimilitud. La autosimilitud es la propiedad que tienen algunos objetos de tener la misma estructura al completo que si los vamos observando a escala menor (es decir, el total tiene una estructura similar a la de partes más pequeñas, y esa propiedad sigue manteniéndose por mucho que aumentemos la lupa o el microscopio con el que lo miremos). En el conjunto de Cantor mostrado arriba, el intervalo [0, 1] sigue apareciendo (de menor longitud, claro) en cualquiera de las etapas en que nos fijemos. Si nos fijamos en la siguiente etapa (dos segmentos y un hueco en medio), esa misma estructura se repite, duplicada (una en el tercio izquierdo; la otra en el tercio derecho) en la siguiente etapa. Y así sucesivamente. Aprovechando esa regularidad, se define la dimensión fractal.
Para entender la idea, vamos a hacer algunas analogías. Imaginemos un cuadrado (el de color naranja de la imagen). Es un objeto con dimensión 2. Supongamos que triplicamos cada lado para hacer un cuadrado el triple del inicial. ¿Cuántos cuadrados del mismo tamaño que el inicial aparecen? En efecto, 9. Eso responde a la sencilla igualdad: 9 = 3D donde 9 es N, el número total de cuadrados que han aparecido del tamaño del inicial, 3 es la escala nueva que hemos introducido (el triple del inicial), y D es la dimensión fractal. En el caso anterior D se obtiene fácilmente, D = 2, que es el valor de la dimensión. El nuevo cuadrado, igual que el inicial, tiene dimensión 2. Si tomamos un cubo, y triplicamos sus lados en las tres direcciones posibles (ejes OX, OY, OZ), obtenemos 27 cubos semejantes al inicial, verificándose que: 27 = 3D De modo que la dimensión resulta ser D = 3, como ya sabíamos. Empleemos el mismo argumento para el conjunto de Cantor. El número de partes N con las que nos quedamos respecto al conjunto inicial al hacer cada iteración es 2; por otra parte, como dividimos el segmento original en tercios, inicialmente el conjunto se divide en tres partes iguales. Por tanto 2 = 3D Para despejar la dimensión fractal D de esa igualdad, tomamos logaritmos a ambos lados de la igualdad, quedándonos log 2 = log 3D= D log 3 Recuerden que una propiedad de los logaritmos es log pq = q log p, si p > 0 Despejando D, se tiene que
Otras particularidadesEl conjunto de Cantor encierra otras muchas sorpresas. Por ejemplo, pensemos en su longitud. El intervalo inicial, [0, 1], tiene longitud 1. En la primera etapa, quitamos 1/3 de dicho intervalo, es decir, L1= 1 – 1/3 = 2/3. En la siguiente etapa, eliminamos 2/9 (1/9 en cada “zona”; véase la imagen previa). Eso nos lleva a que L2 = 2/3 – 2/9 = 4/9. Vamos construyendo de este modo la siguiente sucesión:
Se trata de una sucesión de tipo geométrico (un número elevado a la potencia n-ésima) de razón menor que 1 (r = 2/3). Por tanto, cuando n tiende a infinito, su valor tiende a cero. ¿Y eso que indica? Que el conjunto es de medida nula (no olvidemos que los términos de la sucesión son longitudes). Y de ahí se deduce que no puede contener a ningún conjunto de otra longitud que no sea cero. Por otra parte, también se puede caracterizar el conjunto de Cantor mediante números, ya que los puntos que van quedando “vivos” en cada iteración, tienen la particularidad de que, escritos en base 3 de numeración, son todos aquellos que no utilizan el dígito 1 en su expresión decimal. También se llega al conjunto de Cantor mediante el límite de una sucesión de funciones contractivas. Parece muy complicado, pero no lo es tanto. De hecho, la mayor parte de los conjuntos fractales son el atractor (la función límite a la que convergen, por decirlo en dos palabras) de un sistema de funciones iteradas. En otra de estas reseñas se lo cuento. Comprueben si lo han entendidoOtro de los fractales más conocidos es la llamada curva copo de nieve (por su parecido con esa forma) de von Koch. Se genera del siguiente modo: se parte de un triángulo equilátero, y en cada iteración, se dividen sus lados en tres partes iguales. Después sobre la parte central, se vuelve a formar un nuevo triángulo equilátero. En la primera iteración, como ven en la imagen, esto se hace en cada uno de los tres lados del triángulo inicial. Pero ya en la siguiente, se hace eso mismo en cada uno de los segmentos rectos que han ido apareciendo. La cosa en seguida se multiplica (ya ven sólo en la quinta etapa la cantidad de “protuberancias” que van apareciendo. El ejercicio que les propongo es que intenten probar que la dimensión fractal de uno de sus lados únicamente es
Además, el área que encierra es finita (pueden probar que es 8/5 del área del triángulo equilátero original) y, sin embargo, su perímetro (la longitud de sus lados) es infinito. En esos lados por otra parte no existe un solo punto en el que la curva sea diferenciable (no tiene tangente en ningún punto). La curva que define esos lados es continua, pero no derivable en ningún punto. Fue definida en 1904 por el matemático sueco Helge von Koch. Como ven, no son ni muchos menos objetos de ayer: ¡¡tienen más de un siglo!! Geometría fractal
Estas curvas existían mucho antes de que se acuñara el término “fractal”, pero luego se constató que cuadraban perfectamente en esa idea. En torno al año 1975, el matemático polaco-galo-norteamericano Benoît Mandelbrot (1924-2010) trabajaba sobre iteración de funciones complejas. Este campo de investigación lo habían desarrollado los franceses Gaston Julia y Pierre Fatou a principios del siglo XX. Descubre conjuntos de la complejidad de los indicados antes, y se plantea organizar con rigor, fundamentar todo este tipo de “objetos extraños”. Ante su visión gráfica (los ordenadores van mejorando en estos tiempos), piensa que muchos de estos conjuntos se ajustan más a la naturaleza que las líneas rectas o las curvas de la geometría tradicional.
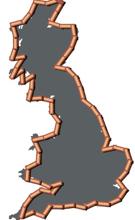
Concretamente escribe un artículo en el que se plantea cómo medir con precisión la costa de Gran Bretaña, haciendo el siguiente razonamiento: si uno observa desde un avión cómo es la forma (a una altura que le permita verla bien), la puede aproximar mediante trazos rectos de un modo más o menos aproximado. Pero si va bajando, observará como el perfil de la costa se va volviendo más rugoso, más escarpado, y debería hacer nuevas mediciones. Pero si baja más, y más, hasta que nuestro rostro esté a la altura del borde, se percatará de que, en realidad, esa costa está llena de rocas con formas caprichosas, agujeros, arena, etc., de modo que, si incluso pudiera verlo microscópicamente, los granos de arena dan otro perfil distinto. Ningún objeto matemático definido hasta ese momento puede dar tal precisión. Y ahora tampoco, pero los objetos fractales se aproximan más. En sus propias palabras: «Las nubes no son esferas, las montañas no son conos, las costas no son círculos, y las cortezas de los árboles no son lisas, ni los relámpagos viajan en una línea recta» (introducción del libro 'La Geometría Fractal de la Naturaleza'). Por otro lado, se descubren otros fenómenos naturales de tipo físico (englobados dentro de la llamada teoría del Caos) que tienen cierta coherencia dentro de dicha geometría fractal. Por tanto, podríamos concluir que los fractales pretenden modelizar fenómenos y objetos presentes en la Naturaleza. Si nos fijamos en la hoja de helecho, dibujada mediante fractales, de la imagen adjunta, bien podríamos pensar que está tomada de la realidad. Pues no, está generada por ordenador mediante iteración de funciones. Si luego le aplicamos efectos como color, sombra, textura, etc., podemos hacerla pasar perfectamente pon una hoja real. En el cine, por ejemplo, se han utilizado este tipo de técnicas para simular paisajes (¿recuerdan la presentación de La isla mínima, película dirigida por Alberto Rodríguez en 2014? Eran imágenes fractales), lugares de otros planetas inexistentes, etc. Aunque los fractales no se quedan en la simulación de paisajes. Existen técnicas de comprensión de datos basadas en fractales que ahorran bastante tamaño (y por tanto espacio) en imágenes digitales. Pero por hoy, es suficiente.
Alfonso J. Población Sáez es profesor de la Universidad de Valladolid y miembro de la Comisión de divulgación de la RSME. El ABCDARIO DE LAS MATEMÁTICAS es una sección que surge de la colaboración con la Comisión de Divulgación de la Real Sociedad Matemática Española (RSME) |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |







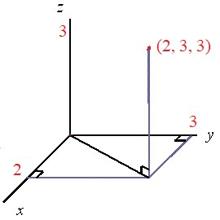 La intersección de los tres ejes es el origen (O), y a cada eje le asignamos un sentido (a la derecha del origen, los valores positivos; a su izquierda, los negativos). En la imagen tendríamos situado el punto (2, 3, 3). Esta terna de números metidos entre paréntesis serían las coordenadas de ese punto. Cualquier objeto que nos rodea (nosotros mismos), podría definirse punto a punto e incrustarse en ese sistema de ejes coordenados. Su dimensión es, por tanto, 3.
La intersección de los tres ejes es el origen (O), y a cada eje le asignamos un sentido (a la derecha del origen, los valores positivos; a su izquierda, los negativos). En la imagen tendríamos situado el punto (2, 3, 3). Esta terna de números metidos entre paréntesis serían las coordenadas de ese punto. Cualquier objeto que nos rodea (nosotros mismos), podría definirse punto a punto e incrustarse en ese sistema de ejes coordenados. Su dimensión es, por tanto, 3.