 Solución al desafío matemático de la Lotería de Navidad 2021: compartir es recíproco
Solución al desafío matemático de la Lotería de Navidad 2021: compartir es recíproco |
 |
 |
 |
|
El País, 21 de Diciembre de 2021 Más de un centenar de lectores han enviado sus respuestas, el 84% de ellas correctas. Pero no todos han seguido el mismo camino para encontrar la solución Ya hay solución para el desafío matemático que como cada año propone EL PAÍS en colaboración con la Real Sociedad Matemática Española con ocasión del Sorteo de la Lotería de Navidad. Recordemos que el desafío consistía en demostrar que el número de quienes comparten suerte en Navidad con una cantidad impar de personas es par. Para resolverlo, lo que vamos a hacer es considerar, para cada persona, el número de gente con la que comparte suerte, y sumar todas estas cantidades. En el ejemplo sencillo que dimos al proponer el desafío, esta suma sería 3 (Ana) + 2 (Cristina) + 2 (Eva) +1 (Pedro) + 0 (Andrés) = 8, que es par. Esto no es un accidente: en todos los casos, si sumamos los números que nos dicen con cuánta gente comparte suerte cada jugador, esa suma es par. Esto se puede comprobar de varias maneras. Quizás la más sencilla es observar que las comparticiones son recíprocas, y eso obliga a que sean un número par. Así lo ha expresado el lector José O. en su solución: “Vamos a suponer que cada vez que dos personas comparten lotería lo declaran a las autoridades entregando un contrato con sus nombres. Como cada contrato contiene dos nombres, el número total de nombres escritos en los contratos es el doble que el número de estos y, por tanto, una cantidad par”. Esta es la clave para resolver el desafío, que, expresado de otra manera, consiste en demostrar que en la suma en cuestión hay una cantidad par de sumandos impares. Para verlo observamos que, si sumamos sólo los sumando pares, obtenemos una suma par. Como suma total-suma de sumandos pares=suma de sumandos impares, y par-par=par, también tiene que ser par la suma de los sumandos impares. Pero (pedimos disculpas por el nuevo trabalenguas) la única forma de que una suma de números impares dé un número par es que sea par la cantidad de sumandos, que es lo que queríamos demostrar. Hemos recibido soluciones que muestran que la suma los números que nos dicen con cuánta gente comparte suerte cada jugador es par de maneras diversas: con otras metáforas, haciendo una tabla,… Queremos recoger una idea que también utilizan bastantes de las respuestas: representar la relación “¿con quién comparto suerte?” mediante lo que se conoce como un grafo. Cada persona que juega a la Lotería de Navidad la veremos como un punto (un vértice del grafo), y uniremos dos vértices por una línea (una arista del grafo) si las correspondientes personas comparten suerte. Como muestra, el grafo que representa nuestro ejemplo sería este (la imagen está tomada de la solución que ha enviado Juan Carlos L.): 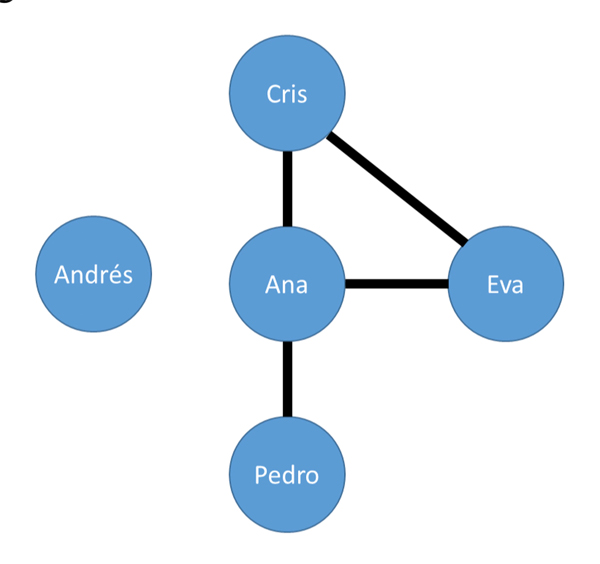 Gráfico enviado Juan Carlos L. en su solución del desafío matemático de la navidad 2021. Esto sería otro posible ejemplo, con 34 personas compartiendo suerte: 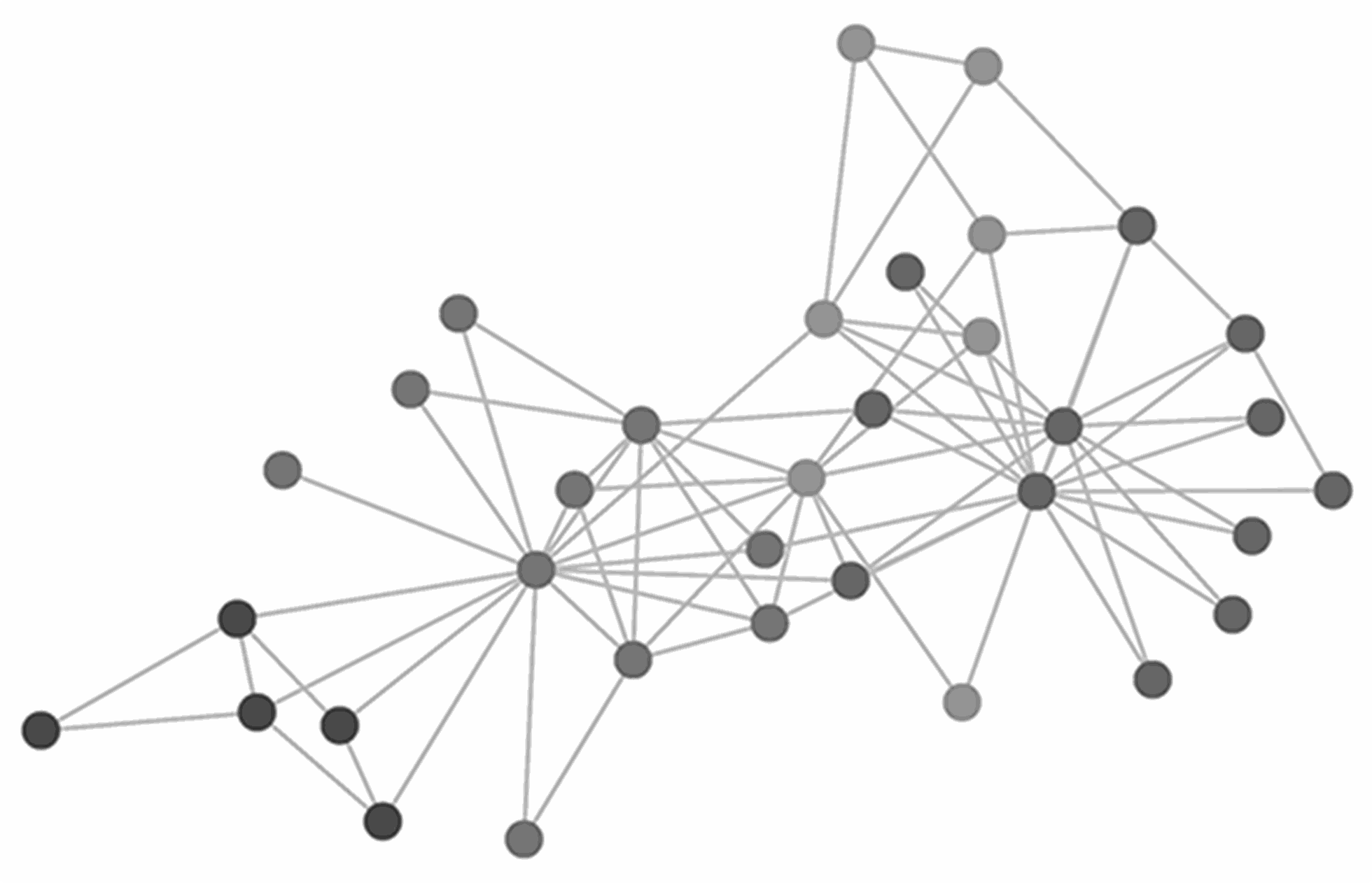
No podemos dibujar el grafo que realmente representa el compartir suerte, porque, aparte de que no lo conocemos exactamente, tendrá varios millones de vértices (uno por cada persona que juega a la Lotería de Navidad) y, posiblemente, algunos cientos de millones de aristas. Aun así, podemos hacer la siguiente observación, válida para cualquier grafo. El número de personas con las que un vértice (una persona) comparte suerte coincide con el número de aristas que llegan a esa vértice. Como cada arista toca a dos vértices, la suma de todos esos números es dos veces el número de aristas del grafo, por lo que la suma es par. Recuperamos así, por otra vía, el resultado básico para resolver el desafío. No nos resistimos a señalar que versión para grafos de nuestro desafío se conoce como el lema de los apretones de manos. Lo demostró en 1736 el insigne matemático Leonhard Euler y tiene numerosas aplicaciones. Varios lectores han seguido un camino algo distinto: han demostrado que, si llamamos I al número de quienes comparten suerte con una cantidad impar de personas, la paridad de I no cambia si dos personas que no compartían suerte deciden compartir. Es decir, la paridad de I es lo que en matemáticas llamamos un invariante. Veámoslo. Para abreviar, diremos que una persona es par/impar si comparte suerte con un número par/impar de personas. Supongamos que Eva y Pedro no compartían y deciden compartir - Si tanto Eva como Pedro eran pares, al añadir la nueva compartición los dos pasan a ser impares. Por tanto I pasa a ser I+2 y su paridad no cambia. - Si tanto Eva como Pedro eran impares, la nueva compartición hace que los dos pasen a ser pares. Por tanto a I pasa a ser I-2 y, de nuevo, su paridad no cambia. - Si Eva es par y Pedro impar (o viceversa), con la nueva compartición Eva pasa a impar y Pedro a par, con lo que I permanece constante. Miramos ahora cómo evoluciona la paridad de I desde el momento inicial, cuando nadie ha comprado todavía ningún número y por tanto todos comparten con 0 personas. No hay entonces ninguna persona impar, por lo que I=0, par. A medida que se van compartiendo números I va cambiando pero, como hemos visto, se mantiene su paridad, y por tanto I será siempre par, como nos proponía el desafío. Esta vía del invariante es la que han seguido, entre otros, Julia V. E., que lo ha hecho, como nosotros, añadiendo comparticiones, y ha dado una elegante demostración por inducción; Daniel R., de Karlsruhe (Alemania), que, en vez de añadirlas, ha ido quitando comparticiones; o Fernando G. V., que lo ha contado como una historia. Sentimos no poder mencionar a todas las personas que han enviado soluciones correctas (alrededor del 84% de las más de cien recibidas en el plazo marcado), pero sí queremos destacar dos que han presentados sus argumentos de manera diferente: César C. que, desde Londres, en lugar de considerar cuántos números comparte cada persona, se ha fijado en cuántas personas comparten cada número (¡seguimos con los trabalenguas!); y Mercedes A. M. quien, en vez de quitar “comparticiones”, ha ido quitando personas y ha dado, quizás inconscientemente, un argumento de descenso infinito. Tres de los autores de soluciones válidas recibirán, por cortesía de la RSME, sendos ejemplares del libro Demostraciones con encanto. Un viaje por las matemáticas elegantes, de Claudi Alsina y Roger B. Nelsen, que forma parte de la Biblioteca Estímulos Matemáticos que la sociedad publica conjuntamente con Editorial SM. Son Enrique T., Isabel O. E. y Rafael R. Confío en que hayáis disfrutado con el desafío y agradezco los mensajes que enviáis junto a las soluciones, que son un incentivo para seguir proponiendo desafíos matemáticos, incluso en estos tiempos complicados. En nombre de EL PAÍS, de la RSME y en el mío propio, os deseo felices fiestas (disfrutadas con precaución), suerte mañana con la lotería y, sobre todo, salud. Adolfo Quirós Gracián es profesor de la Universidad Autónoma de Madrid y director de La Gaceta de la Real Sociedad Matemática Española. |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |






