Enero 2022: Juegos con coordenadas (I)
Enero 2022: Juegos con coordenadas (I) |
 |
 |
 |
| Escrito por José Muñoz Santonja | ||
| Sábado 01 de Enero de 2022 | ||
1. Esas matemáticas cotidianas.Los que nos dedicamos a las matemáticas y, en especial, a su enseñanza, somos conscientes de que hay una parte de la población que siente un rechazo visceral hacia esa materia. Muchas veces esta animadversión se ha gestado en los años escolares, en los que la asignatura de las matemáticas resultó un amargo camino por el que transitar, posiblemente porque la enseñanza que recibieron de esa materia fue sesgada y no se les llegó a mostrar su belleza, su interés y su total aplicabilidad en nuestra vida cotidiana. Dado que su formación y aprendizaje en esa materia fue deficiente, hay personas que llegan a pensar que las matemáticas no sirven para nada, salvo quizás la parte aritmética para el manejo corriente de la economía doméstica. Lo curioso es que esas mismas personas utilizan habitualmente la geometría de la que vivimos rodeados, aplican aunque quizás de una forma intuitiva conceptos de azar, aún en el caso de no pararse a calcular probabilidades, aceptan la información mediante gráficas estadísticas que cada vez son más abundantes en los medios de comunicación. Basta pararse un momento a pensar y puede ser evidente que la construcción, las industrias, el diseño, las comunicaciones de todo tipo serían inviables sin las matemáticas. Hasta el punto, que el estado de alarma en que se escribe este artículo tiene una serie de medidas de prevención, que se basan en reglas matemáticas para afrontarlas, respecto a aforo de establecimientos, distancia entre personas, medidas de temperaturas, cuarentenas, etc… Un aspecto que suele pasar muy desaparecido es el relacionado con el tema que traemos hoy. Las coordenadas cartesianas. Si se pregunta a cualquier persona aislada de las matemáticas si en su vida cotidiana utilizan coordenadas, como las que vieron en los ejes que estudiaron en la escuela, la respuesta unánime sería que no, pero no tenemos más que expresar nuestro desacuerdo. Hay muchas situaciones en las que, aunque no seamos consciente de ello, trabajamos con algún tipo de coordenada. Por ejemplo, y evidente para los que nos dedicamos a la enseñanza, los pupitres en una clase están normalmente situados en filas y columnas, por lo que el alumnado se sienta llevando aparejado un par de coordenadas. De la misma manera, en algunas fábricas o empresas, los lugares donde trabajan los empleados también están asignados a filas y columnas de mesas de trabajo, basta fijarse en algunas noticias donde aparecen empresas textiles y se ven a los operarios colocados según un sistema de coordenadas. Pero aunque esto nos parezca un poco rebuscado, pensemos en cualquier conocido que vive en determinada calle y en un número, y dentro del edificio vive en el 4ºC, lo que no deja de ser unas coordenadas. Pero es que además nuestra butaca en cualquier teatro o cine también viene determinada por unas coordenadas. Y para no alargar el tema, sólo reseñar que hoy en día nos movemos con más soltura y facilidad gracias al GPS, que se basa fundamentalmente en las coordenadas. Los que enseñamos en niveles no universitarios, somos conscientes de que la representación en un sistema de coordenadas es fundamental para poder hacer representaciones gráficas, y también sabemos las dificultades con las que se encuentran muchos alumnos cuando se enfrentan por primera vez a la representación en un sistema de ejes, con las confusiones de ordenadas entre sí. Por ello, hay muchas actividades y juegos para practicar el aprendizaje de este concepto. El objetivo de este artículo es mostrar algunos de esos juegos, intentando seleccionar los que, a nuestro modesto entender, son menos usuales o conocidos de los que se encuentran normalmente en internet. La mayoría de estos juegos estarían englobados dentro de un bloque de lápiz y papel, pues suele ser manualmente como colocamos los puntos en los ejes. Algunos de ellos se podrían realizar directamente sobre una trama de puntos, pero en nuestro caso lo interesante no es el juego en sí, lo que deberemos procurar es que en todo momento los jugadores indiquen las coordenadas de los puntos que van colocando, pues eso es lo que va a reforzar la práctica con los ejes y sus coordenadas. Vamos pues a divertirnos y aprender jugando. 2. Pasatiempos con coordenadas.Vamos a comenzar con una actividad que siempre es gratificante, la resolución de un pasatiempo. Ya hemos incluido en otros artículos ejemplos de retos que aparecen en revistas o periódicos, y que tenían que ver con el tema tratado. Los que nos dedicamos a recopilar pasatiempos desde hace décadas, sabemos que no es normal encontrar pasatiempos relacionados con las gráficas y las funciones, pero a veces se encuentra alguna curiosidad. En primer lugar tenemos un pasatiempo que nos recuerda a los crucigramas y en el que hay que extraer una frase a partir de las coordenadas que nos dan, y que corresponden a unos ejes donde están situadas las letras que forman la frase. Es un pasatiempo encontrado en El Pequeño País, un suplemento que llevó el diario El País en su oferta de fin de semana entre 1981 y 2009, y que es un banco impresionante de pasatiempos matemáticos.
Imagen 1: Suplemento El Pequeño País. El segundo, ya más dirigido a público adulto, pertenece a la revista QUO. Yo lo recogí de un suplemento de pasatiempos que salió con el número 77 de febrero de 2002 y que recogía pasatiempos aparecidos en los números anteriores. En él, el reto es encontrar cómo se asigna la información para asignar las coordenadas a cada una de las letras.
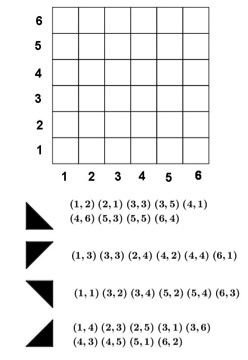
Imagen 2: Revista QUO. 3. Dibujos en cuadrículas.Como actividades de acercamiento a la definición de ejes cartesianos, hay varias que se pueden utilizar para preparar ese nuevo concepto. Una manera corriente en la que nos encontramos con elementos que vienen determinados por dos datos, es en los crucigramas o en recuadros similares a los que hemos visto en el primer pasatiempo. Yo suelo comenzar trabajando con cuadros divididos en cuadrículas y que utilizan una estructura similar a lo anterior, aunque siempre me gusta que en ambos ejes aparezcan números, en lugar de letras en uno de ellos. Muchos sabemos la dificultad que entraña distinguir entre el punto (2, 4) y el (4, 2), cosa que no ocurre si los datos son (B, 4) y (D, 2), por ello siempre suelo trabajar con ambos ejes numéricos. El primer problema que se puede plantear es dibujar puntos en los ejes, y para ello lo mejor es dar una serie de coordenadas que den lugar a un dibujo reconocible. En internet es posible encontrar decenas de actividades en las que conseguir una figura más o menos reconocible, como alguna construcción geométrica o personajes como el Pato Donald o Astérix, incluso más recientes como Bob Esponja, los Minions o Picachui. 3.1. Figura con polígonos.Hace tiempo encontré una plantillaii en la que la variedad era que no se dibujaban puntos sino polígonos, aunque daba igual, pues el objetivo es colorear las piezas en el lugar correspondiente. Aunque en el original se utilizaban varios colores, yo lo prefiero sólo en blanco y negro. A continuación, podemos encontrar un ejemplo de esta actividad.
Imagen 3: Dibujo en cuadrícula. Aunque no lo especifique la imagen, lo que debemos hacer es dibujar uno de los cuatro triángulos en las casillas correspondientes a las coordenadas que le acompañan. Entre las actividades que encontramos en la red, para trabajar con coordenadas, podemos hallar dos maneras de trabajar, una es la vista antes, dar una serie de coordenadas y dibujar los puntos, o en nuestro caso los triángulos, pero a mí siempre me gusta complementarlo con la otra opción, dar un dibujo ya hecho y extraer las coordenadas. Esto es muy frecuente en los retos para alumnos más pequeños, en los que se colocan en los puntos de la cuadrícula elementos reconocibles, como juguetes o frutas y se deben indicar las coordenadas. En la propuesta de la imagen 3 aparece un dibujo simétrico por lo que hay veces que se dibuja la misma pieza con coordenadas simétricas, como (1, 2) y (2, 1), aunque no siempre es así. De todos modos, me gusta intentar plantear figuras que no sean simétricas. En la siguiente imagen, el objetivo es sacar las coordenadas que corresponden a cada una de las cuatro piezas triangulares.
Imagen 4: Extraer coordenadas de un dibujo. Para acabar este apartado hay otro modo en el que trabajo para extraer coordenadas de un dibujo, pero complicando un poco el trabajo. Les indico una figura que deben dibujar en unos ejes cartesianos, y después indicar las coordenadas de los puntos que forman los vértices de esa figura. Como ejemplo, se debe dibujar en el sistema de ejes cartesianos usual el tangram siguiente, y después escribir las coordenadas de los vértices de los polígonos.
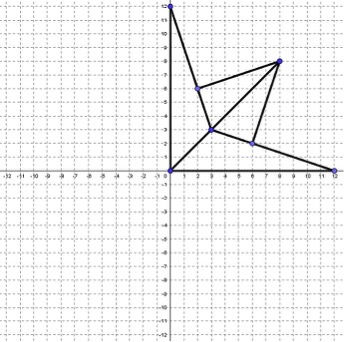
Imagen 5: Dibujar polígonos en los ejes. El alumno debe fijar el tangram en la cuadrícula, de forma que todos los puntos que son vértices de las piezas correspondan a coordenadas enteras. Se puede obviar esta regla, pero en ese caso se complica la solución, porque entonces los puntos pueden quedar en lugares más complicados de reconocer sus coordenadas. Si se quiere simplificar el proceso se les puede indicar que el lado del cuadrado grande debe ser 4 o múltiplo de 4, para que todo quede correcto. 3.2. Coordenadas y algo más.El dar una serie de pares coordenados y dibujar algo que sea reconocible, puede combinarse con trabajar otros conceptos matemáticos para repasar. Una actividad interesante es proponer a los alumnos que elijan tres puntos y que sobre ellos construyan un triángulo, de forma que se anoten un punto si el triángulo es escaleno y tres puntos si es isósceles. De la misma forma, colocan tres puntos y se anotan un punto si es acutángulo, dos si es obtusángulo y tres si es rectángulo. Según el nivel del alumno con el que se trabaje, hay una forma de complicar este sencillo ejercicio y es obligar a que los tres puntos que se eligen para hacer un triángulo no tengan, ninguno de ellos, ni la primera coordenada, ni la segunda iguales. De esta forma, dos puntos no pueden estar en la misma horizontal ni en la misma vertical, y hay que buscar con más cuidado los puntos. Hay otra actividad que me parece interesante. Se le pide al alumno que dibuje los puntos y las rectas que van de uno a otro de cada pareja y que se indican a continuación: (12, 0) a (3, 3); (3, 3) a (0, 12); (0, 0) a (12, 0); (0, 0) a (0, 12); (0, 0) a (8, 8); (6, 2) a (8, 8) y (2, 6) a (8, 8). Nos quedaría un dibujo como el que aparece en la imagen siguiente.
Imagen 6: Dibujo antes de simetrías. El siguiente proceso es dibujar los puntos y las líneas correspondientes a las simétricas de las anteriores respecto al eje de abscisas, lo mismo respecto al eje de ordenadas y por último los simétricos respecto al origen, obteniéndose al final algo que se asemeja a la Rosa de los Vientosiii. Los alumnos deben anotar en su cuaderno las coordenadas de todos los puntos que vayan dibujando como simétricos de los dados por el profesor. Si una vez acabados de representar los nuevos puntos y unidos se colorean los triángulos alternos, queda un dibujo bastante aparente.
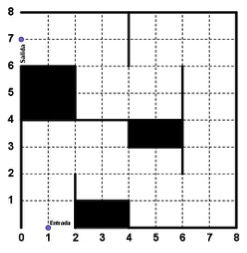
Imagen 7: Rosa de los Vientos aproximada. 4. Recorre el laberinto.Uno de las primeras actividades que se pueden utilizar para manejar coordenadas de una forma diferente a las usuales es la de recorrer un laberinto. Al jugador se le entrega un laberinto similar al de la imagen, y se le pide que indique por cuáles puntos coordenados hay que pasar para recorrer el laberinto desde la entrada hasta la salida. Es decir, hay que comenzar en el punto (1, 0) y terminar en el (0, 7).
Imagen 8: Tablero con la forma a capturar. Si se quiere indicar todos los puntos nos encontramos con 29 posiciones por las que se pasa, por lo que la resolución se hace un poco pesada. Lo usual es pedir que indiquen los puntos en que se debe de cambiar de dirección al moverse por el laberinto. De esa manera, desde el (1, 0) llegaríamos al (1, 3), después el (3, 3) y así sucesivamente. Es decir, mientras nos desplacemos en una línea recta sólo se indican el principio y final de esa línea. Se pueden tener varios laberintos preparados con mayor extensión y mayor grado de dificultad y los que acaben más rápidamente que hagan otras opciones. Aunque de entrada es un solitario, es decir, para que cada alumno trabaje con el tablero presentado, se puede convertir en un juego de parejas. En este caso se entrega a cada uno una cuadrícula y cada jugador se encarga de dibujar el laberinto que tendrá que resolver el contrario. En estos casos se encuentra uno con auténticos laberintos churriguerescos. El jugador que consigue resolver el laberinto propuesto, se anota tres puntos y se pueden proponer varios laberintos. El jugador que propone un laberinto debe tener la solución, es decir, la secuencia de puntos por los que se debe pasar. Si se comprueba que su solución es errónea se le penaliza con un punto. Hasta ahora hemos visto juegos que son básicamente solitarios, aunque puedan hacerlo entre varios alumnos. Vamos a pasar al apartado de juegos entre contrincantes. 5. Localiza la palabra.Hemos visto en el primer pasatiempo del artículo, una actividad en la que había que conseguir una palabra a partir de sus coordenadas. A partir de ese pasatiempo y de un tablero más completo localizado en internetiv, construí el siguiente juego para dos jugadores. Se juega con un tablero como el siguiente.
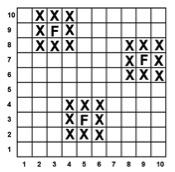
Imagen 9: Tablero de Localiza la palabra. Las letras están colocadas aleatoriamente manteniendo la proporción con que aparecen en español las distintas letras. Hay algunas que no aparecen ya que su porcentaje es menor del 1% como son la k, la ñ, la x y la w. Y hay ocho letras que sólo aparecen una vez: f, g, h, j, q, v, y, z. La forma más simple de jugar es la siguiente: uno de los jugadores piensa una palabra, por ejemplo de cinco letras, y busca las coordenadas de las letras en el tablero. Le indica al contrario esas coordenadas y el contrario debe reconstruir la palabra. Si lo consigue se anota un punto, si no lo consigue el primer jugador, debe mostrar qué palabra era y si se ha equivocado el indicar las coordenadas de la palabra buscada (algo que no es raro al principio). Entonces se le anota un menos uno, es decir, se le quita un punto de los que consiga. Se puede jugar a un determinado tiempo o una determinada cantidad de jugadas, por ejemplo, cada jugador propone cinco palabras. Gana quien tenga al final más puntos, aunque lo normal es quedar en empate. Una forma de complicar el juego anterior, y que suele gustar a los alumnos es que al indicar las coordenadas de las letras no se obligue a que las coordenadas vayan ordenadas según las letras de la palabra, y de esa manera, puede darse el caso de que la ordenación de las letras dé lugar a distintas palabras. Por ejemplo, un jugador lanza la palabra con las coordenadas (0, 2), (7, 0), (1, 10), (8, 4) y (9, 6). Así obtenemos las letras D, N, A, O, S con lo que se pueden formar las palabras: danos, sonda, ondas, donas. El jugador que busca la palabra se anota un punto al escribir una palabra del idioma español formada con esas letras, y si coincide con la que había pensado el contrario se anota dos puntos más. Para ello puede presentar todas las palabras que pueda construir con esas letras, y si entre ellas está la propuesta se anota esos dos puntos extra. ¡Ojo! no se anota un punto por cada palabra, su puntuación es la jugada en un punto por mostrar una palabra válida en nuestro idioma, y dos más si esa palabra era la buscada, independientemente de la cantidad de palabras que muestre. Para que no haya posibilidad de engaño, quien lanza la palabra debe anotarla en su hoja para mostrarla posteriormente. Para no alargar la jugada, debe limitarse el tiempo en el que el jugador está buscando posibles palabras que se puedan formar con esas letras, por ejemplo, dos minutos a partir de que ha localizado las letras. Hay otro modo de jugar inverso al anterior que es más simple, pues uno de los dos jugadores no tiene porqué utilizar las coordenadas cartesianas siempre. El jugador que lanza la palabra simplemente dice una con una determinada cantidad de letras, por ejemplo, dice la palabra RENTA y el contrario debe indicar ordenadamente cinco pares de coordenadas que correspondan a esas letras, y se anota un punto si es correcto. Si la palabra tuviese letras repetidas, por ejemplo CASPA, las coordenadas de la letra A debe ser distintas en ambas casos, es decir, no se puede utilizar las mismas coordenadas estando la misma letra colocada en lugares distintos. Solo en el caso en que se utilice una letra repetida que sólo esté una vez en el tablero, por ejemplo VIVAS, entonces se pueden repetir las coordenadas de la V. En esta modalidad se debe fijar un tiempo límite, por ejemplo tres minutos, para localizar las coordenadas. Si no se ha logrado, pasado ese tiempo, el jugador que ha lanzado la palabra debe indicar las coordenadas de la palabra, y si no las encuentra se le penaliza con dos puntos. Por ejemplo, puede darse el caso de que un jugador diga la palabra CAÑOS que es imposible encontrar en el tablero ya que no hay ninguna ñ. En esta modalidad, los jugadores con más conocimiento del vocabulario pueden poner en apuros al contrario lanzando palabras en las que haya letras que sólo aparece una vez, como HOGAR, FEROZ o VORAZ. Hay una tercera modalidad de juego que he propuesto algunas veces. Siempre lo hago después de haber jugado como he explicado anteriormente, y suelo plantearlo para aquellas parejas que acaban más rápidamente el juego anterior. Durante un tiempo estipulado, por ejemplo cinco minutos, los jugadores intentan localizar la palabra más larga posible formada por letras que sean contiguas en vertical u horizontal sobre el tablero, es decir, las coordenadas ordenadas de las letras deben varias solamente en una de las dos coordenadas que será una unidad más o menos. Por ejemplo, la palabra ROTARE formada por las coordenadas (0, 3), (1, 3), (2, 3), (3, 3), (3, 4) y (3,5). Una vez pasado el tiempo, los jugadores muestran, mediante sus coordenadas, cada uno la palabra más larga que hayan encontrado. Quien tenga la solución se anota tres puntos. Se puede dejar ahora dos o tres minutos para encontrar otra palabra, descartando las dos que se han encontrado antes y repetir el proceso las veces que los jugadores quieran, siempre dejando menos tiempo que los cinco minutos iniciales. Cuando terminen gana, como es lo normal, quien haya acumulado más puntos Una forma de presentar el juego, dado que el objetivo es trabajar con las coordenadas, es jugar de las distintas formas e ir acumulando puntos en cada partida, ganando al final el que haya conseguido más. Como dijimos al principio, en todos los casos si las coordenadas no son correctas se pierde el turno, o si es quien la ha propuesto se le ponen puntos negativos. 6. Ataque al fuerte.Posiblemente la actividad más extendida para trabajar lúdicamente las coordenadas cartesianas en clase, es el juego de los barquitos. Suponemos que es bastante conocido y además en la red se pueden encontrar, ya no decenas, si no cientos de páginas, en cualquier idioma, en donde se explica el juego e incluso se dan plantillas personalizadas para jugar en ellas. Por tanto, vamos a presentar aquí un juego no tan conocido. Hasta tal punto está poco extendido que no he conseguido encontrar ni una sola referencia en internet y sólo lo he encontrado referenciado en el libro de Jordi Deulofeu que está en las referencias. El profesor Deulofeu lo titula Fuertes y adjudica su creación en 1975 a Harry Wollerton, del que solo he encontrado otra referencia en un libro de Martin Gardner, indicando que presentó varios juegos en la revista británica mensual Games & Puzzles. Igual que el juego de los barcos, cada jugador dispone de dos cuadrículas de 10x10, una para colocar sus fuertes y otra para sus disparos. En esto se simula al otro juego, pero ahí se acaban las similitudes. Cada jugador coloca en su tablero tres fuertes. Los fuertes son cuadrículas de 3x3 que no pueden estar en contacto entre sí ni horizontal, ni vertical ni diagonalmente. En la casilla central de esa cuadrícula se coloca una F para indicar el cuartel general. Vemos un ejemplo de distribución de fuertes en la siguiente imagen.
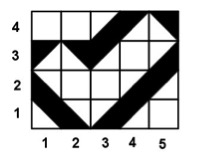
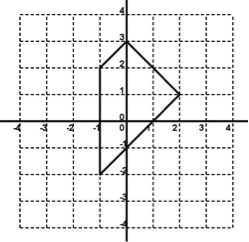
Imagen 10: Tablero de Ataque al fuerte. Los disparos también se realizan de distinta forma. Un jugador indica una casilla y una dirección, y el contrario les responde el número de casillas de fuertes que están en esa dirección, sin contar el número de fuertes que han sido tocados. Por ejemplo dispara indicando la casilla (10, 1) y la dirección Noroeste, a lo que el contrario, que tiene el tablero anterior, respondería 2, pues hay dos casillas en esa dirección donde hay partes de los fuertes. Si en la siguiente jugada dijera (4, 1) Norte, la respuesta sería 6. De forma alterna, los jugadores van lanzando disparos hasta que uno de ellos crea tener localizados los fuertes y, en lugar de lanzar un nuevo disparo, debe indicar las coordenadas de los cuarteles generales de los tres fuertes. Si los acierta los tres, gana la partida, en caso contrario pierde. Esa es la forma como lo plantea el profesor Deulofeu. Yo prefiero dar la posibilidad de que vayan descubriendo la zona central de los fuertes uno a uno. Es decir, en un determinado momento el jugador que cree conocer la disposición de un cuartel general indica su posición. Si falla, pierde el turno, si acierta puede hacer dos cosas, o arriesgarse a indicar otro cuartel general o lanzar otro disparo. Se continúa el juego hasta que uno de los jugadores ha descubierto todos los cuarteles generales del contrincante. 7. Juego de capturar las formas.Entre los juegos que son versiones adaptadas del juego de los barquitos, encontré uno en la página de mathwirev donde se encuentran varios recursos curiosos para trabajar coordenadas. Veamos una adaptación de ese juego. Se enfrentan dos jugadores cada uno de ellos con dos tableros como en los barquitos. En la imagen siguiente vemos un tablero con coordenadas desde -4 a 4 aunque se puede ampliar o, si se quiere, reducir solo al primer cuadrante. Uno de los tableros es para que el jugador dibuje su forma y los disparos del contrincante y el otro para colocar sus propios disparos, igual que en los barquitos. Cada jugador dibuja en su tablero una forma que debe ser un cuadrilátero pero que tenga alguna propiedad, es decir, puede ser: cuadrado, rectángulo, rombo, romboide o trapecio. En la imagen vemos dibujado un trapecio rectángulo.
Imagen 11: Tablero con la forma a capturar. A continuación, cada jugador en su turno lanza un par de coordenadas y el contrario debe indicar si ese punto contiene un vértice, está en la línea de un lado, está dentro de la figura o fuera de la figura. Se continúa hasta que un jugador consigue localizar los cuatro vértices, en cuyo caso debe indicar qué tipo de cuadrilátero es. Si acierta los vértices se anota tres puntos y dos puntos más si dice el nombre correcto del cuadrilátero. Si se equivoca pierde el turno, y se continúa hasta conseguir localizar correctamente una de las formas. 8. Y todavía más.Como suele ocurrir cuando preparo un artículo para estas páginas, aparte de los juegos que he utilizado anteriormente suelo buscar documentación sobre juegos del mismo tipo. Y cuando me doy cuenta tengo más material del que tenía previsto, por lo que me quedo corto para abarcar todo lo que tengo guardado. Una vez más me ha ocurrido y por eso veremos un segundo artículo con juegos diversos de coordenadas, incluyendo algún juego en tres dimensiones. 9. Referencia.DEULOFEU, Jordi (2001): Una recreación matemática: historia, juegos y problemas. Planeta, Barcelona. Colección Planeta Prácticos.
Notas:[i] En el blog de Ana García Azcárate pueden encontrarse varias entradas para dibujar figuras mediante coordenadas, desde ejemplos simples como un monigote, hasta ejemplos más complicados como un zorro o el Picachu que hemos citado. [ii] En la siguiente dirección hay varias plantillas para hacer dibujos de colores con este sistema. [iii] La idea para esta especie de Rosa de los Vientos la extraje de la siguiente dirección, en la que se dibuja completamente la estrella. [iv] Se puede adquirir un cuadernillo con el material en que se basa libremente el juego en la dirección: [v] La parte correspondiente a juegos con coordenadas es la siguiente: |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |