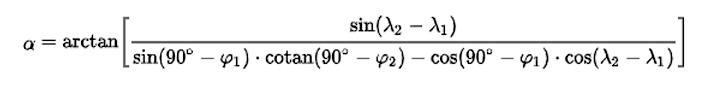80. (Febrero 2022) La alquibla en al-Ándalus
80. (Febrero 2022) La alquibla en al-Ándalus |
 |
 |
 |
| Escrito por Ángel Requena Fraile | ||||||||||||||||||||||||||||||
| Martes 01 de Febrero de 2022 | ||||||||||||||||||||||||||||||
|
(Mihrab de la Mezquita de Córdoba) ¿Anómala orientación cordobesa?La Mezquita de Córdoba es la obra maestra del Califato Omeya de al-Ándalus. La orientación de la mezquita califal cordobesa ha sido un enigma. Quizá lo siga siendo. No lo es ahora para una persona tan autorizada como David A. King que ha decidido dar el asunto por zanjado tras muchos años de dedicarse al tema y modificar su primera hipótesis. La orientación del edificio hacia el amanecer del solsticio de verano (y ocaso del de invierno) hace que su perpendicular coincida con la orientación del eje de la Kaaba: el surgir de la brillante estrella Canopus. Este dato llevó inicialmente a King a considerar que era la alquibla correcta. Recientemente King ha encontrado una explicación más simple y la ha desarrollado en The enigmatic orientation of the Great Mosque of Córdoba explained (2018): la mezquita se orienta según la cuadricula romana de Colonia Patricia (la urbs nova). Cuando admiramos el bellísimo mihrab cordobés no pensamos en cosas tan prosaicas como que la orientación del rezo no es el que nos dirige a La Meca, casi 80º E, sino de tan solo de 30º. El templo se adaptó a la dirección preexistente del cardo /decumanos romano. Las prescripciones religiosas islámicas fueron dinamizadoras de la matemática, tanto para la aritmética como para la astronomía geométrica. El reparto de herencias, el calendario lunar, el inicio del ramadán, la hora de los rezos o la propia alquibla eran estimulantes para el estudio. Los andalusíes del siglo XI llegaron a desarrollar la más alta matemática del momento. La Mezquita es una muestra inicial de ese desarrollo: arte y ciencia suelen darse la mano. Córdoba no fue excepcional: la alquibla, la dirección a La Meca de los cinco rezos de los creyentes musulmanes, de las mezquitas de al-Ándalus minusvaloró sistemáticamente la orientación en todos los casos que hemos estudiado. El cálculo de la latitud siempre fue sencillo, una vez conocida la eclíptica, pero el de la longitud siguió siendo un problema clásico hasta bien entrado el siglo XVIII. El cálculo de la alquiblaLa dirección a la Kaaba desde el lugar de referencia no fue un problema complejo desde el punto de vista teórico para los astrónomos musulmanes. Las técnicas de Hiparco y Ptolomeo eran suficientes y, además, los sabios musulmanes las mejorarían y fundieron con los avances de la India. Desde el punto de vista práctico la dificultad era la determinación y tabulación segura de la longitud del lugar en relación con las coordenadas esféricas de La Meca. La alquibla del lugar del rezo no es otra cosa que el acimut, el ángulo que forma el meridiano del lugar con el circulo máximo que une con la Kaaba, y se obtiene mediante la expresión:
Siendo a el acimut, φ1 y λ1 las coordenadas geográficas del lugar del rezo, y φ2, λ2 las coordenadas de la Kaaba. Las φ son las latitudes y las λ las longitudes. La fórmula se obtiene del tercer grupo de Bessel de la trigonometría esférica aplicada al triángulo formado por el Polo Norte, La Meca y el lugar. Se conocen dos lados (las colatitudes) y el ángulo comprendido: se busca el acimut de la Kaaba desde el lugar. Hoy estamos más acostumbrados a trabajar vectorialmente con geometría analítica: se trata de calcular el ángulo diedro que forman el plano meridiano con el plano de la geodésica que pasa por el lugar y La Meca. El cálculo se puede hacer de forma aproximada y suficiente mediante el astrolabio, valiendo cualquier planisferio. Una vez situada La Meca en el astrolabio solo hay que anotar el acimut (Anexo). Los astrolabios universales, con plano de proyección meridianos, son muy sencillos de usar y pueden tener marcado el paralelo de La Meca como parte de la eclíptica. El astrónomo Al-Battānī (c. 858 – 929) (latinizado Albatenius) dio un método simplificado reduciendo el triángulo esférico a uno plano pero la aproximación solo vale para los lugares próximos, que no es el caso de al-Ándalus. En la práctica había tablas con las coordenadas de las ciudades más pobladas y que servían para su territorio. Al final todo se reduce a una buena tabla de longitudes geográficas.
(Astrolabio de Ibrahim ibn al-Sahlí (Toledo - 1067). Museo Arqueológico Nacional)
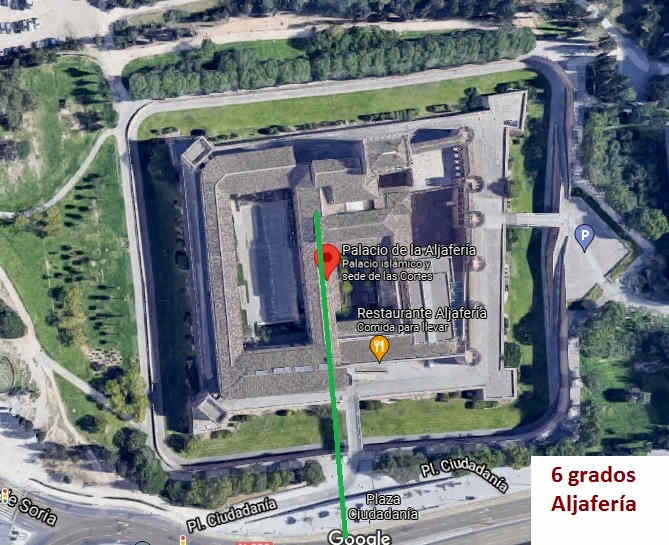
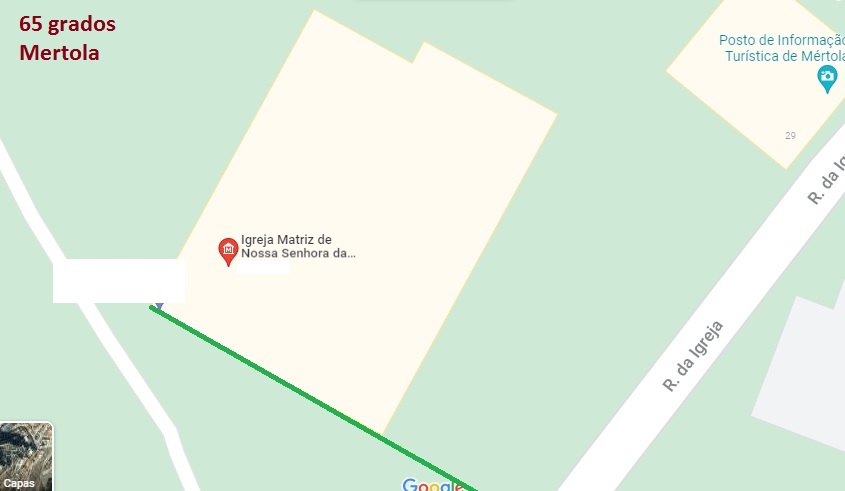
Determinación de las longitudesEl procedimiento tradicional para obtener las longitudes relativas entre lugares es aprovechar los eclipses lunares. El método ya aparece en el tratado clásico de la astronomía hindú Surya Siddhanta, una recopilación que se iba modificando pero que ya lo incluía cuando fue vertido al árabe en el siglo IX. Tanto Albatenius como al-Biruni (c. 973 – 1050) ya usaron los eclipses lunares y realizaron las medidas con notable precisión. En tierra firme se puede esperar un eclipse pero en el mar el problema de la longitud subsistió. Cristóbal Colón aprovecho dos eclipses lunares para medir, uno en el segundo viaje [Saona - 1494] y otro en el cuarto [Jamaica - 1504] pero la precisión no fue muy buena. España fue en 1567 el primer país que ofreció recompensar a quien resolviera el problema. Y todavía en 1714 los ingleses mantuvieron el premio y el desafío. Las distancias de estrellas a la Luna, la declinación magnética y hasta las lunas mediceas de Júpiter (Galileo) parecían los procedimientos más prometedores. Al final fue un relojero, Hamilton, y no un astrónomo, quien ofreció la solución más fácil: un reloj preciso en el navío. Ya Hiparco había relacionado la longitud y la hora. La alquibla en al-Andalus La orientación de los Mihrab en al-Ándalus se limitan a dirigir el rezo más o menos hacia el sudeste pero minusvalorando en general el Este. Los cálculos actuales nos dicen que la alquibla oscilaría entre los 70º y los 84º. Así Zaragoza requiere 72º y Mertola, en Portugal, 82º. Curiosamente la bien conservada mezquita portuguesa es la mejor orientada de las estudiadas.
(Mezquita de Mertola. Alentejo) La moderna mezquita de la M30 en Madrid está orientada a 76º que es la dirección correcta pero ninguna de las antiguas se aproxima. Hemos seleccionado algunas de las mezquitas u oratorios islámicos mejor conservados, algunas incluso con su mihrab. Al tratarse de una aproximación se ha utilizado la aplicación google maps pues buscamos solo orden de magnitud y no exactitud.
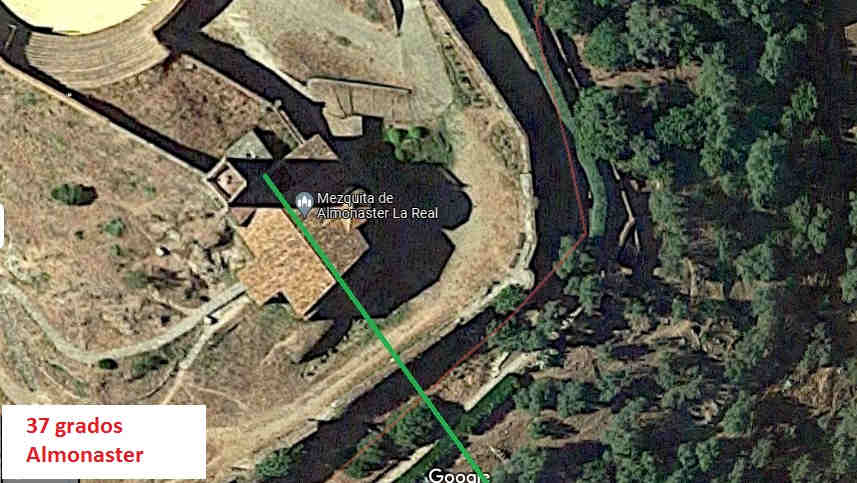
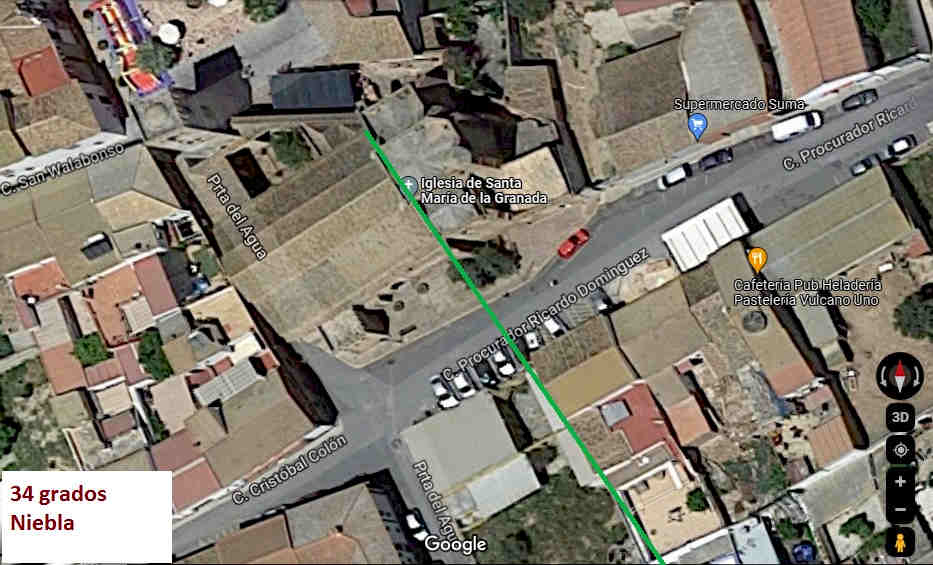
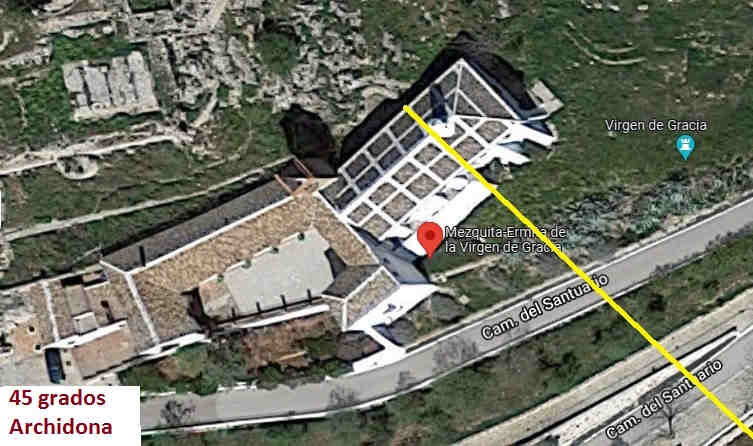
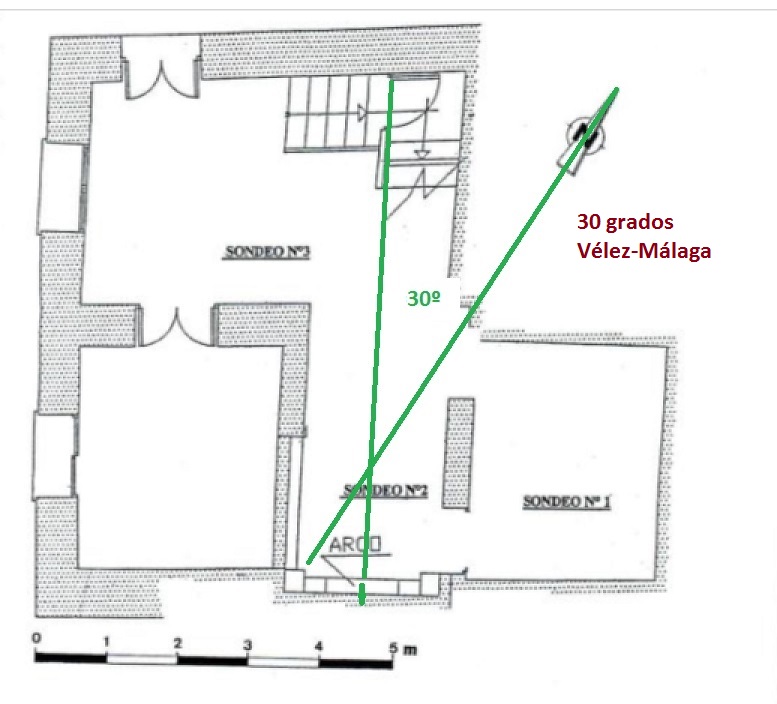
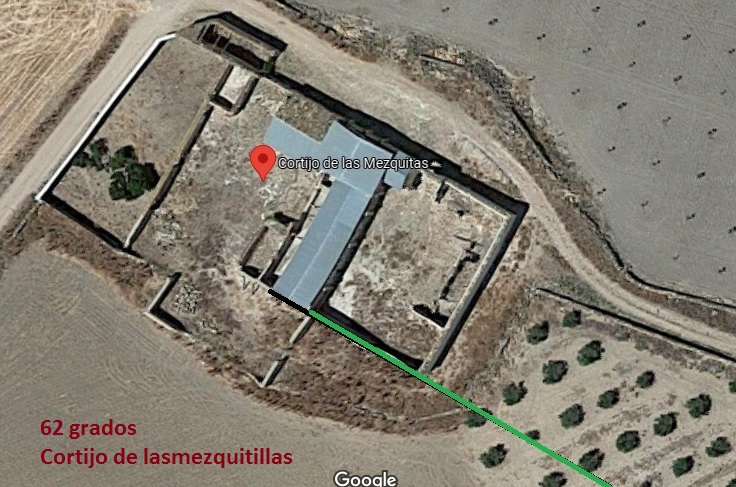
Conocía los 30º de la anómala orientación de la Mezquita Aljama de Córdoba y me sorprendió cuando estudie, por proximidad, la orientación del mihrab extramuros de Vélez-Málaga: también 30º. Otras muestras ponen de manifiesto la heterogeneidad y que no hay patrón: más al Sur que al Este cuando tenía que ser al revés. La multitud de mezquitas transformadas en iglesias hace que tanto el estudio como la precisión pueda ampliarse muchísimo pero consideramos que la muestra es significativa: el precepto de la dirección del rezo fue laxo en al-Ándalus. La razón principal debió ser la falta de precisión de la diferencia de longitudes a lo que se sumaría la edificación anterior o la orografía del terreno.
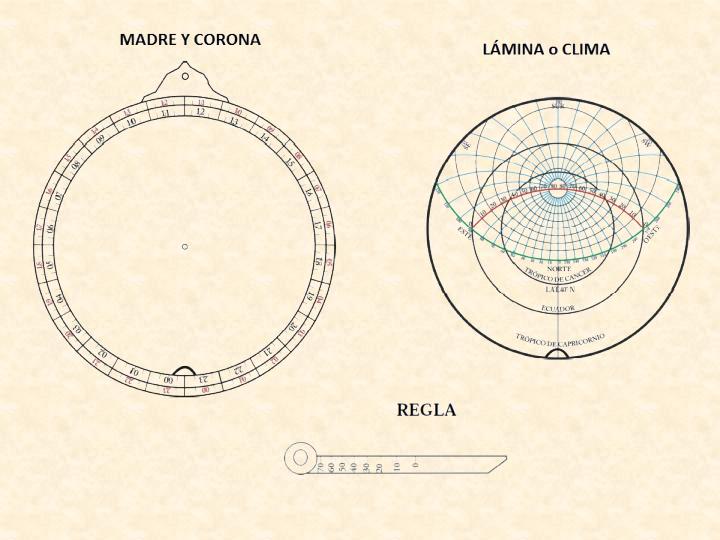
ANEXO: Acimut de La Meca con astrolabioCualquier planisferio puede servir para calcular la alquibla. Vamos a hacerlo con un astrolabio plano corriente. Aprovechamos parcialmente el modelo -para construcción- de la Asociación Valenciana de Astronomía. Un astrolabio es un sencillo e ingenioso mecanismo para cambiar el sistema de referencia: una forma de pasar de ángulo horario y declinación del astro a altura y acimut, las coordenadas locales.
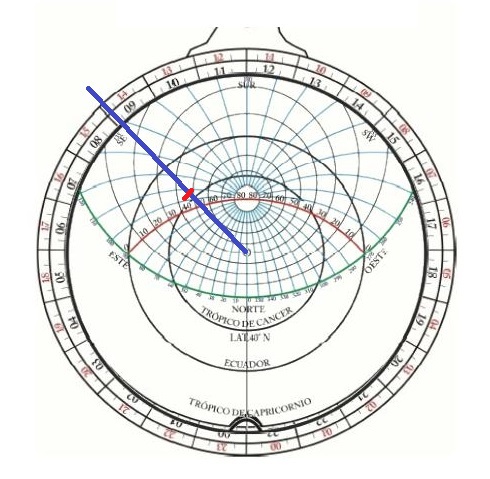
La madre es donde se alojan las láminas, la red, la regla y la alidada (al dorso). Para la alquibla no hace falta la red – las posiciones relativas son fijas- ni la alidada ya que no hay que medir alturas de ningún astro. De la madre nos interesa la corona que señala las horas: cada hora son 15 grados. La lámina tiene dibujados los almicantarates (paralelos al horizonte local) que nos dan la altura y las verticales (círculos máximos locales) que nos darán el acimut. La regla tiene marcados los paralelos geográficos, sus números marcados son las declinaciones, en nuestro caso nos sirve para marcar la latitud de La Meca. El proceso a seguir es el siguiente:
|
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |