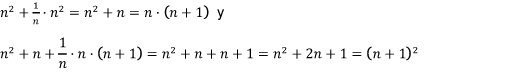Mayo 2022: Ritmomaquia. Un juego medieval
Mayo 2022: Ritmomaquia. Un juego medieval |
 |
 |
 |
| Escrito por José Muñoz Santonja | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Domingo 01 de Mayo de 2022 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
En el año 2000 se comenzó con esta sección de juegos, inicialmente acogida en el seno de la revista SUMA, editada por la Federación Española de Sociedades de Profesores de Matemáticas, y tras cerrarse la sección en 2014, los artículos se acogieron en la sección correspondiente de la página divulgamat, en donde han salido apareciendo artículos nuevos. En todos estos años siempre se han incluido juegos más o menos actuales, que han servido como recursos para plantear actividades e incluso investigaciones en el aula de matemáticas. Pero hoy vamos a modificar ese enfoque. Lo que se presenta hoy es un antiguo juego aritmético que en la actualidad es bastante desconocido, posiblemente debido a lo complicado de sus reglas de juego. Según algunos investigadores, como el profesor de la Universidad de Barcelona José M. Núñez, al que nos referiremos en varias ocasiones, se puede considerar a Ritmomaquia como el primer juego occidental creado para la enseñanza de las matemáticas. Básicamente, este juego es una batalla entre dos contrincantes que disponen de una serie de fichas, en las que cuentan tanto la forma geométrica como el número asociado. Para capturar piezas del oponente hay que hacer una serie de cálculos aritméticos e incluso para ganar la partida hay que conseguir colocar una serie de números en distinto tipo de progresión. Pero además, entre los valores de las fichas vamos a encontrar números poligonales y piramidales. Antes de presentar el juego debemos poner en antecedentes históricos la época en que tuvo vigencia, y en qué teorías matemáticas se basa. 1. Ritmomaquia, el mejor juego aritmético durante siglos.Este juego tiene muy diversos nombres, según los autores que lo referencian: rithmomachia, rythmomaquia, arithmomachia, rithmomachy. Se considera que el nombre tiene procedencia griega. La palabra estaría compuesta de dos vocablos griegos, el primero sería una especie de combinación entre arithmos y rythmos que haría referencia al número o al aspecto rítmico, más bien a la armonía como proporción, y el vocablo machia que equivaldría a batalla. Por ello, se suele traducir como la “batalla de la armonía”, aunque Tomas Moro, en su obra Utopía hace referencia a este juego como “la batalla de los números”. En el libro de Moro se enfrenta este juego a los llamados juegos nefastos, como cartas o dados, que estaban prohibidos en Utopía, mientras sí se permitían el juego de números y otro en el que se enfrentaban las virtudes y los vicios. Lo cierto es que el juego era también conocido como “El juego de los filósofos”, pues ritmomaquia era un juego desarrollado en los ambientes ilustrados, especialmente escolásticos. Algunos autores medievales asociaban la invención del juego a los pitagóricos, pero no existe ningún texto griego que corrobore esa opinión. Los investigadores fijan en el primer tercio del siglo XI, más concretamente dan la fecha de 1030, cuando un monje llamado Asilo, del monasterio alemán de Würzburg, hizo la primera referencia a este juego, y por ello consideran que pudo ser su creador. El primero que al parecer escribió un pequeño tratado, llamado Hermanni tirmomachia, sobre el juego es el benedictino Hermann Contractus (1013 – 1054) cronista alemán que se dedicó a la música, pero también a otras ciencias como la Astronomía o la Geometría. El juego comenzó a implantarse en los monasterios y fue pasando de forma casi oral de unos estudiosos a otros hasta que poco a poco, y a lo largo de los siguientes siglos, hubo diversos autores que escribieron sobre el juego, mostrando cada uno de ellos unas reglas algo diferentes como veremos más adelante. La opinión generalizada es que el juego se inventó para desarrollar los conceptos de la aritmética de Boecio, del que hablaremos más adelante. Al parecer el juego se creó dirigido a los alumnos de las escuelas de monasterios. Según la historiadora Ann Moyer, especialista en juegos de la Edad Media y que en 2001 publicó un libro sobre la Ritmomaquia, el juego era por un lado un recurso para el estudio de la obra aritmética de Boecio, pero también pretendía educar en valores morales presentes en la filosofía de Boecio. De ahí, que la iglesia apostara por este juego frente a otros considerados más licenciosos. Durante una amplia época, llegó a tener más fuerza que el ajedrez, que aunque no era un juego prohibido por la Iglesia, tampoco estaba considerado un entretenimiento virtuoso. Estamos hablando de una época medieval en la que el plan de estudios de las Universidades se reducían a las siete artes liberales agrupadas en dos grupos de materias, el trívium (gramática, dialéctica y retórica) y el cuadrivium (aritmética, geometría, música, astronomía) ya estructurado por los pitagóricos. En poco tiempo el juego se expandió por Alemania y Francia, dando el salto a Inglaterra en el siglo XIII, donde se extendió también con mucha fuerza. El propio filósofo Roger Bacon lo aconsejaba como una actividad muy adecuada para sus alumnos. Al principio, los textos eran breves y las referencias al juego era casi meramente sobre su existencia y su interés, incluso en algunos textos se consideraban ya conocidas las reglas y los valores de las fichas. Durante los siglos siguientes hubo varios autores que escribieron obras donde ya se presentaban manuales, con mayor explicación, sobre el juego. Entre ellos podemos citar, por su cercanía, al jienense Juan Pérez de Moya (1512? - 1596), quizás el más importante autor de libros de texto de matemáticas de la época. En particular en su obra de 1562 llamada Diálogos de Aritmética Practica y Especulativa[1], aparte de contener ya un tratado de álgebra, habla de ritmomaquia, citándolo por cierto como juego pitagórico, indicando sus reglas y las piezas que lo forman. Al entrar en el Renacimiento el juego comienza a perder importancia, y llega a desaparecer. Posiblemente al cambiar los planes de estudio y comenzar a tomar fuerza el álgebra, ritmomaquia como juego para practicar la artimética perdió interés. De todos modos, hay que tener presente que aunque al principio el juego se utilizaba como recurso educativo, poco a poco se comenzó a jugar por el mero placer de practicarlo, pero siempre dentro de ámbitos eruditos no llegando a extenderse más allí. En siglos posteriores, en concreto en el XIX y a comienzos del XX[2] hubo varios intentos de volver a poner de actualidad el juego pero sin mucho éxito. Ya en este siglo, el profesor Tomás Guardia Ortega, en ese momento profesor de la Universidad Central de Venezuela, comenzó a estudiar el juego y promovió la creación del Club Venezolano de Ritmomachia[3], intentado poner de moda el juego. El club se creó como un Grupo de Extensión en la Facultad de Ciencias de dicha Universidad. Se redactaron unas reglas, algunas de ellas desconocidas hasta el momento, y se organizaron incluso campeonatos de juego. Desgraciadamente a partir del año 2016 no hay ningún movimiento en la página del club, no sabemos si coincidiendo con la marcha del profesor Guardia, auténtico alma mater del proyecto, a Estados Unidos o por otras causas. 2. La aritmética de Boecio.Como comentamos en el epígrafe anterior, el juego de Ritmomaquia se creó para desarrollar las aritmética de Boecio, por ello es importante estudiar algunos aspectos de este matemático y de su obra para que podamos entender los números que se utilizan en el juego, y que son un poco extraños si no se explica su construcción. Se ha considerado a Anicio Manilo Severino Boecio (480 – 524) como el mejor matemático romano de la antigüedad. Esto no es contradictorio con que muchos autores lo considerasen como un matemático mediocre, pues todo el que tenga un poco de idea de la historia de la matemática, sabe la irrelevancia que significó el periodo romano en esa disciplina. Boecio fue también filósofo, poeta y político y su principal aportación a las matemáticas fue la traducción, muchas veces simplificada, de obras griegas. Igual que Euclides con sus Elementos fue el soporte, durante siglos de la enseñanza de la Geometría, Boecio fue autor de referencia durante cerca de mil años en la enseñanza de la aritmética gracias a su libro De arithmetica donde traducía la Introductio atirhmetica del pitagórico Nicómano de Gerasa (60 – 120). Quizás los lectores hayan visto alguna vez la siguiente imagen, una de las ilustraciones del libro Margarita Philosophica escrito por Gregor Reisch (1504) donde se recrea a la idealizada aritmética contemplando una delirante batalla entre Pitágoras, realizando cuentas con un ábaco, y Boecio que realiza las cuentas con las cifras indo-arábigas. No sólo es delirante porque a los dos personajes los separan alrededor de diez siglos, sino porque esas cifras no empezaron a extenderse por Europa hasta el Renacimiento, varios siglos después de la muerte de Boecio.
Imagen 1: La batalla de la aritmética. Tomada de Wikipedia[4]. En el libro de aritmética Boecio no hace propiamente matemáticas, se dedica a organizar y explicar los tipos de proporciones estudiados por los pitagóricos. Para entender el valor asignado a las piezas del juego y la forma de jugar, es necesario tener presentes esos tipos de proporciones por lo que a continuación vamos a explicar, no todas las que utiliza Boecio, sino aquellas que vamos a utilizar posteriormente en la explicación de los números, que aparecen en el juego. Vamos a utilizar como referencia el texto del profesor José M. Núñez. En la aritmética, Boecio divide a los números entre iguales y desiguales. Estos últimos los divide a su vez en dos categorías, mayores y menores. Dentro de las mayores se encuentran varias posibilidades que son las que luego van a aparecer en la organización de los valores de las fichas y son los siguientes. Multiplex: cuando un número contiene un número entero de veces a otro número. Sería lo que conocemos como múltiplo. Superparticularis: cuando un valor contiene un número entero y una parte de él. Por ejemplo, 9 sería un superparticularis de 6 pues es igual a 6 más su mitad, es decir, 9 = (1 + ½) · 6. Superpartiens: cuando el valor es igual a un número entero más varias partes de él. Por ejemplo, 28 sería superpartiens de 16 pues se obtendría de sumarle a 16 las ¾ partes de 16, es decir, 28 = (1 + ¾) · 16. Sería similar al anterior con la diferencia de que en el anterior se le suma el número multiplicado por una fracción de numerador 1, mientras que en éste el numerador es distinto de 1. Aunque Boecio presenta muchas más proporciones, básicamente estas tres serán las que utilicemos en las fichas de Ritmomaquia, como veremos además, a cada proporción corresponde una figura geométrica distinta en la ficha. 3. ¡Pues en mi casa jugamos así!Antes de comenzar con el juego en sí hay un detalle que me gustaría comentar. Seguramente les habrá pasado en alguna ocasión el ponerse a jugar con algún amigo o en un ambiente social a un determinado juego, y de pronto descubrir que se estaban jugando con reglas distintas, por lo que no es raro que alguno de los jugadores suelte la frase que titula este epígrafe. Eso es un poco lo que ocurre con Ritmomaquia. Aunque suele haber unanimidad en el valor de las fichas, a partir de ahí no hay forma de encontrar dos autores que coincidan en el resto de reglas y elementos. Al principio la expansión del juego podría ser de forma oral y hasta que no se produjo la invención de la imprenta no aparecieran textos fiables, pero con cambios entre unos autores y otros. En la página de acanomas[5], dedicada a la explicación de juegos, muchos de ellos históricos, aparece una entrada en la que se habla de los principales autores medievales, y se hace una tabla comparativa entre ellos comprobando la variación de reglas existentes. Por no ponerse de acuerdo no hay unanimidad ni en el tamaño del tablero. Es rectangular de ancho ocho casillas, pero el largo varía desde 10 hasta 16. Las fichas tienen la misma forma y un jugador las lleva blancas y otras negras, pero hay autores que consideran que las fichas tienen dos colores, como las tradicionales fichas del juego Othelo, de forma que al capturar una de ellas se le puede dar la vuelta e incorporarlas al propio juego. Tampoco se ponen de acuerdo en el movimiento de las fichas. Ni siquiera en las capturas. Cuando un jugador captura una pieza contraria, hay autores que no mueven la pieza atacante sino que retiran la atacada del tablero, mientras que otros ocupan la posición de la ficha capturada. Sí suele haber unanimidad en los tipos de capturas y en las formas de conseguir la victoria, que hay de distintos tipos. En esta ocasión nos hemos decidido por tomar las reglas del exhaustivo artículo de José M. Núñez, complementándolo con la referencia del conocido libro de Bell y Cornelius sobre Juegos con tablero y fichas, a pesar de que los dos textos tienen diferencias. 4. Los valores de las piezas del juego.Ritmomaquia es un juego atípico, dentro de los de tablero y fichas, pues no es simétrico. Los jugadores tienen el mismo número de fichas pero el valor que tienen en ellas son muy diferentes. Cada jugador tiene un total de 24 fichas, una de ellas tridimensional y las restantes planas. Un jugador juega con fichas blancas y el otro con negras. Se suele decir que la blancas son las pares y las negras son las impares, pero esto es porque los números de los que se parten son pares en las blancas e impares en las negras, pero veremos que los dos jugadores tienen la misma cantidad de valores pares e impares en sus fichas. La forma de las fichas tiene relación con las proporciones que vimos anteriormente. Hay 8 fichas redondas que corresponderían a la proporción multiplex, otras 8 triangulares donde irían los números superparticularis y 7 cuadradas con las valores superpatiens. Hay una última pieza que correspondería a una pirámide formada por acumulación de fichas de distintos valores. Vamos con la descripción de las fichas. El jugador con blancas comienza con los primeros números pares 2, 4, 6 y 8 y a continuación sus cuadrados 4, 16, 36, 64. Esas serían las fichas redondas. Las triangulares comienzan sumándole a estas cuatro últimas la proporción correspondiente al inverso de los números originales, es decir, 6 = (1 + ½)·4, 20 = (1 + ¼)·16, 42 = (1 + 1/6)·36 y 72 = (1 + 1/8)·64. En las otras cuatro fichas triangulares se repiten las proporciones anteriores pero con los números que se han obtenido antes. Así tendríamos: 9 = (1 + ½)·6, 25 = (1 + ¼)·25, 49 = (1 + 1/6)·42 y 81 = (1 + 1/8)·72 Las fichas cuadradas se obtienen de las triangulares, añadiendo a los números anteriores las fracciones 2/3, 4/5, 6/7 y 8/9 de esos números, fracciones que son los valores originales divididos por el siguiente entero, y realizando lo mismo con los valores obtenidos. De esta manera los números que van en las fichas cuadradas son: 15 = (1 + 2/3)·9; 45 = (1 + 4/5)·25; 91 = (1 + 6/7)·42; 153 = (1 + 8/9)·81 25 = (1 + 2/3)·15; 81 = (1 + 4/5)·45; 169 = (1 + 6/7)·91; 289 = (1 + 8/9)·153 Para que queden más estructuradas colocamos las piezas en una tabla.
Las fichas negras tienen exactamente las mismas proporciones pero partiendo de los cuatro primeros impares sin considerar el 1. De esa manera las fichas serían las siguientes:
Se puede apreciar que cada jugador tiene valores que se repiten, a veces en distinto tipo de fichas y que también se repiten algunos valores en las fichas de los dos jugadores. Como antes he hablado de las disparidades en las reglas, hay quien pueda pensar que ya me estoy contradiciendo con lo que había dicho antes, pues he hablado de una pieza tridimensional. Eso es porque, en cada jugador hay una pieza, dentro de las cuadradas, que tienen forma de pirámide y está, a su vez, formada por varias fichas. Son los valores 91 para las blancas y 190 para las negras. Esos valores son realmente números piramidales, pues son suma de cuadrados de números consecutivos. Así, 91 = 1² + 2² + 3² + 4² + 5² + 6² mientras que 190 = 4² + 5² + 6² + 7² + 8². En el caso de las blancas, las dos primeras fichas serían redondas, las dos siguientes triangulares y las dos últimas cuadradas. Para las negras, la primera es redonda, las dos siguientes triangulares y las dos últimas cuadradas. Esto es importante pues influirá en la forma de moverse y capturar de esa pirámide. Como las bases de las pirámides son cuadradas es por lo que se engloban dentro de ese bloque. Dado que éste es un artículo sobre un juego para aprender aritmética, es poco ortodoxo por mi parte echar mano del álgebra, pero es una buena forma de ver qué relación hay entre los distintos números que se obtienen en el proceso anterior. Si observamos la primera columna de cualquiera de las tablas, los números que corresponden a las fichas redondas serían n y n². Las triangulares serían:
Y las cuadradas serían:
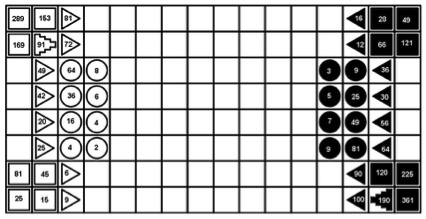
Es decir, los números que forman la primera columna, llamando n al primer valor serían: n, n·n, n·(n+1), (n+1)·(n+1), (n+1)·(2n+1) y (2n+1)·(2n+1), con lo que se puede apreciar una regularidad. Una actividad para practicar, en un determinado contexto, las expresiones algebraicas puede ser hallar la expresión de los restantes números de la tabla. Es fácil porque sería sustituir n por los valores primeros de cada columna, es decir, n+2, n+4 y n+6. Una vez que tenemos las fichas con sus valores, el siguiente paso es colocarlas en el tablero y eso es lo que nos indica la siguiente imagen.
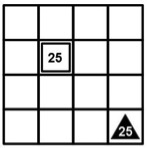
Imagen 2: Tablero y fichas del Ritmomaquia. Nosotros vamos a considerar que el tablero tiene de dimensión 8 x 16, es decir, serían como dos tableros de damas o ajedrez unidos. Hay autores que muestran el tablero en forma de damero, con cuadros blancos y negros como en ajedrez o damas, pero realmente no aporta nada al juego, por lo que es mejor que sean todos los cuadros iguales. Los jugadores se colocan en el extremo pequeño del tablero y las fichas deberían estar mirando al jugador, en la imagen se han puesto de lado para que sean más fáciles de ver, pero deberían de girarse 90º. La anterior es la distribución más usual, aunque hay lugares donde podemos encontrar una colocación diferente de las piezas no redondas, por ejemplo, en el libro de Bell y Cornelius. Hay una cosa curiosa que no suele comentarse, y es que las fichas de los dos jugadores están colocadas de forma simetría respecto al centro del tablero. Es decir, la casilla donde está el primer número de las redondas, triangulares o cuadradas blancas es simétrica, respecto al centro, de donde está colocada la primera ficha correspondiente de las negras, y lo mismo con las demás. Si alguien desea jugar y no se quiere tomar la molestia de construir el tablero y las fichas, se pueden encontrar en internet en forma de pdf descargable[6] para imprimir y recortar. Sólo tienen una pega y es que los colores de las fichas están cambiados, es decir las pares son negras y las impares blancas, justo al revés de lo que proponen la mayoría de los autores. 5. Reglas del juego.Vamos a ver ahora cómo se juega. En primer lugar los movimientos, después las capturas y por último como se gana. Lo último suele ser algo común a todos los autores pero los otros dos elementos suelen presentar disparidad, veamos por tanto lo que propone el profesor José M. Núñez que sigue la versión considerada más completa de Claude de Boissiere de 1554. 5.1. Movimientos de las piezas.Según la figura poligonal de la pieza, el movimiento es diferente. Las piezas redondas pueden moverse una casilla en horizontal o vertical. Las triangulares se mueven dos casillas en diagonal. Las cuadradas se mueven tres casillas en cualquier dirección, horizontal, vertical o diagonal. En el artículo de Núñez se habla de dos, tres y cuatro casillas para el movimiento, pero considerando la casilla de partida, es decir, la casilla donde está la pieza que se mueve. Las pirámides, dado que están formadas por piezas de los tres tipos, puede moverse con cualquiera de los tres movimientos según decida el jugador, siempre que siga teniendo fichas con esa forma. Veremos que es posible capturar piezas sueltas de la pirámide. Si una pirámide ha perdido las piezas redondas, por ejemplo, ya no podrás hacer el movimiento correspondiente a ese tipo de piezas. Las piezas no pueden colocarse en casillas que estén ocupadas. Lo normal es que la ficha no pueda pasar por encima de otra, sea propia o contraria. 5.2. Captura de una pieza del oponente.Hay cuatro formas de capturar una pieza del contrario. Cuando el jugador hace un movimiento, se capturará la pieza del contrario según las posibilidades siguientes. En todos los casos, la pieza que se captura se retira del tablero y la ficha con que hemos capturado no ocupa la casilla donde estaba la ficha capturada. a) Captura por encuentro. Se produce cuando una ficha propia podría con su movimiento correspondiente, ocupar una casilla donde se encuentra una ficha del contrario del mismo valor. Por ejemplo, en la siguiente imagen la ficha negra, en su turno, capturaría a la ficha blanca.
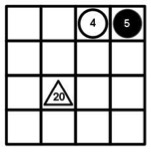
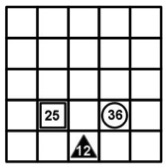
Imagen 3: Captura por encuentro. b) Captura por emboscada. Si un jugador tiene dos fichas que en un movimiento regular pudiesen llegar a la casilla donde se encuentra una del contrario, y con los valores de las dos atacantes se puede conseguir el valor de la atacada, realizando cualquier operación aritmética, se captura la del contrario. Por ejemplo, en la imagen las fichas blancas pueden capturar la negra ya que 20:4 = 5 y la negra está a una casilla de la blanca en horizontal y a dos de la triangular en diagonal.
Imagen 4: Captura por emboscada.
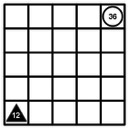
c) Captura por asalto. Esta modalidad se cumple cuando el valor de la pieza atacante multiplicado o dividido por la cantidad de casillas en blanco que hay hasta una contraria, en la dirección de su movimiento, sea igual al valor de la pieza enemiga. En la imagen vemos una situación en la que el triángulo negro captura el círculo blanco pues al estar a tres casillas se verifica que 12 · 3 = 36.
Imagen 5: Captura por asalto. d) Captura por asedio. Una pieza se captura de esta forma si está rodeada por piezas del contrario y no puede moverse. Se suele decir que está rodeada por las cuatro casillas ortogonales o las cuatro diagonales. También se pueden aprovechar las esquinas y los lados del tablero. En la siguiente imagen, la ficha negra es capturada porque no puede moverse.
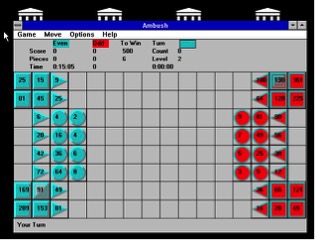
Imagen 6: Captura por asedio. La pirámide puede capturarse por su valor total o por piezas parciales. Podemos, por ejemplo, atacar la pirámide blanca y capturar el triángulo que vale 16. Cuando una pirámide pierde una ficha disminuye su valor, en el ejemplo anterior, la pirámide restante valdrá ahora 75. También si pierde todas las fichas de una determinada forma, por ejemplo las redondas, ya no podrá moverse una sola casilla de forma ortogonal. Si hay disparidad de criterios sobre cómo se mueven las piezas, la locura es saber qué se hace con la pieza capturada. Hay autores que indican que las piezas deben tener dos caras, una blanca y otra negra y que al capturar la pieza el jugador le da la vuelta y la incorpora a su juego. Otros dicen que cuando a un jugador le capturan una pieza puede colocar en su lugar alguna de las que él haya capturado previamente. Como veremos que para ganar se cuentan las piezas capturadas, mi consejo es que la pieza retirada se deje fuera del tablero y una vez que se tenga práctica en el juego se piense en modificar esta opción. 5.3. Cómo ganar en Ritmomaquia.A diferencia de otros juegos, en Ritmomaquia hay muchas formas de ganar la partida, pero no todas tienen la misma categoría, así hay formas de ganar que podríamos llamar “cutres” y otras que serían las “fetén”, que en alguna documentación llaman gloriosas. Para estas últimas tenemos que recordar qué son las progresiones de números. Llamamos progresión aritmética a aquella sucesión de números que se obtienen uno del anterior sumando siempre una cantidad fija llamada diferencia. Sería lo mismo que decir que la diferencia entre dos valores consecutivos es siempre la misma, por ejemplo 2, 4, 6, y 8, cuya diferencia de uno a otro es 2. La progresión geométrica se obtiene cuando un valor es el resultado de multiplicar el anterior por una cantidad fija. Por ejemplo 4, 16, 64, donde el cociente entre dos valores consecutivos siempre es 4. Tres números están en progresión armónica cuando el cociente entre el tercero y el primero es igual que el cociente entre la diferencia de los dos últimos y los dos primeros. Así si tenemos los números a, b y c están en progresión armónica si se verifica que Vamos pues con los tipos de victorias. 5.3.1. Victorias comunes. Antes de jugar se fijan unas cantidades que hay que conseguir para ganar. Las hay de distintos tipos: a) Victoria del cuerpo. Se fijan una determinada cantidad de fichas y el jugador que consigue capturar esa cantidad, independientemente de su valor, es el que gana. b) Victoria de bienes. Se fija un determinado valor y gana el que primero consigue llegar a ese valor con las piezas capturadas. c) Victoria de proceso. Aparte del valor obtenido, se tiene en cuenta las cifras de las fichas capturadas. Así, si un jugador tiene 121 y 49 que suman 170 y el otro jugador tiene 153, 15 y 2, que suman lo mismo, gana el segundo jugador por tener 6 cifras en contra de las cinco del primero. d) Victoria de honor. Gana quien consigue sumar o superar una determinada cantidad, previamente fijada, con una cantidad de piezas capturadas menor que otra cantidad también fijada antes de comenzar. e) Victoria de honor y proceso. En esta modalidad se agrupan los tres aspectos, cantidad que suman las fichas capturadas, números de fichas y número de cifras. 5.3.2. Victorias propias. Como indica el profesor Núñez en su artículo, es unánime la forma de ganar que vamos a ver, pero lo que no está claro es la forma de colocar las fichas. Algunos autores indican que las fichas pueden estar en línea recta, formando un ángulo recto (o un triángulo aunque no sea recto) y si son cuatro fichas se colocarían en los vértices de un cuadrado. Lo que es claro es que no puede haber otras fichas entre las piezas que forman las progresiones que vamos a ver. Tampoco está claro que sea obligatorio que el orden de las fichas sea correcto, es decir, basta que las fichas que estén en línea, o en las otras distribuciones, sean las que forman la progresión. Por último, para ganar es necesario en muchas ocasiones que una de las fichas sea del contrario, pero no está claro cómo se consigue, si puede ser una de las fichas del tablero o tiene que ser una de las capturadas que se vuelve al tablero. Los propios autores medievales eran conscientes de esta inconcreción de las reglas, y no les importaba pues afirmaban que una de las virtudes del juego es que era adaptable al gusto de los jugadores. Lo que sí es uniforme es que la progresión ganadora debe situarse en el campo del contrario. Veamos pues las forma de ganar en esta modalidad. a) Victoria mediocre o magna. Cuando el jugador logra disponer tres fichas en el campo contrario que estén en alguna de las progresiones que hemos señalado anteriormente: aritmética, geométrica o armónica. b) Victoria grande o mayor. Se da cuando se consigue colocar cuatro piezas en posición de forma que contengan dos progresiones diferentes, por ejemplo, aritmética y geométrica. Esto pasaría con las piezas 1, 5, 9 y 25 pues tendría la aritmética 1, 5 y 9 y la geométrica 1, 5 y 25. c) Victoria excelente o excellentisima. Cuando se consiguen cuatro fichas en las que hay las tres progresiones a la vez. Un ejemplo sería el conjunto de piezas 4, 6, 9 y 12 que contiene una progresión aritmética (6, 9 y 12), una geométrica (4, 6 y 9) y una armónica (4, 6 y 12). Una actividad para trabajar las progresiones en este juego consiste en buscar las distintas progresiones que podemos formar con las piezas. En el libro de Bell y Cornelius se indica que sólo hay tres progresiones que puede llevar a la victoria excelente: (3, 4, 6 y 9), (4, 6, 9 y 12) y (15, 20, 30 y 45). También se indica que hay 60 conjuntos de números que incluyen las progresiones aritmética y geométrica, 41 con aritmética y armónica y 15 con geométrica y armónica. Existe una página[7] en la que se pueden encontrar explicadas las capturas y las victorias gloriosas mediante fotografías, aunque hay que tener cuidado porque en los movimientos mete reglas que yo no he visto en ningún otro sitio, por ejemplo unos movimientos como los caballos de ajedrez. En esa página hay un enlace a otra información donde aparecen todas las progresiones aritméticas, geométricas y armónicas que se pueden formar, aunque muchas de ellas se forman con las pirámides disminuidas en alguna pieza. Aparecen, por ejemplo, un total de 35 progresiones armónicas que son las más difíciles de conseguir. 6. Para cerrar el juego.Hemos visto cómo el fundamento principal del juego es la aplicación de las operaciones aritméticas. Debemos volver a recordar que estamos situados en una época medieval en la que la formación del quadrivium se hacía en las universidades, ya que los conocimientos previos, aquellos que los tenían, eran muy básicos. Jugar a Ritmomaquia obliga a realizar las operaciones básicas para poder capturar piezas del oponente, y para ganar hay que tener un manejo claro de las progresiones, por lo que tras jugar, puede ser un incentivo para que los alumnos investiguen y descubran posibilidades de ganar. Como ya hemos dicho, los intentos que ha habido de volver a poner en circulación el juego de nuevo, no han dado buenos frutos, pero eso no quiere decir que el juego haya desaparecido. Existe una aplicación llamada Ritmomachia creada por Julio Cesar León, del club venezolano que hablamos antes, que puede encontrarse en la playstore de algunos móviles. En el año 1994 se creó un juego para PC llamado Ambush que se puede encontrar en internet, en una versión de 2015 y que permite jugar en línea.
Imagen 7: Pantalla del Ambush. Hay que tener presente que tiene cambios respecto a las reglas que hemos indicado. En primer lugar las fichas de cada lado están colocadas de forma simétrica a como hemos visto y los movimientos también cambian algo. A pesar de la dificultad de aprenderse todas las reglas al principio, es un juego interesante y que puede servir para practicar matemáticas. 7. Referencias.BELL, R & CORNELIUS, M. (1990): Juego con tablero y fichas. Labor, Barcelona. NÚÑEZ ESPALLARGAS, J.M. (2004): “La aritmética de Boecio y la Ritmomaquia: teoría y práctica del juego medieval de los sabios”. Anuario de estudios medievales Vol 34, nº 1. CSIC. Versión digital, revisada el 11 de julio de 2020, en http://estudiosmedievales.revistas.csic.es/index.php/estudiosmedievales/article/view/187
Notas:[1] Se puede conseguir en pdf copia del libro en el servicio de publicaciones digitales de la Universidad de Granada. Más concretamente en la dirección siguiente, encontrándose el juego en la página 111 del pdf. [2] En 1911 apareció un artículo en la revista The american mathematical monthly explicando el juego. Puede consultarse en la dirección. [3] La dirección de la página del club es https://rithmomachiaucv.blogspot.com/. En ella puede encontrarse la explicación del juego tal como lo concibieron en el club. [4] En la dirección https://es.m.wikipedia.org/wiki/Archivo:Gregor_Reisch,_Margarita_Philosophica,_1508_(1230x1615).png [5] http://www.acanomas.com/Historia-Juegos-de-la-Antiguedad-y-Edad-Media/623/Historia-del-Rithmomachy.htm [6] http://valby.copenhagenfablab.dk/sites/default/files/projects/game-rithmomachia.pdf [7] https://www.boardspace.net/rithmomachy/english/rules.html |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |