Octubre 2022: Juegos de probabilidad con cartas
Octubre 2022: Juegos de probabilidad con cartas |
 |
 |
 |
| Escrito por José Muñoz Santonja | |||||||||
| Viernes 28 de Octubre de 2022 | |||||||||
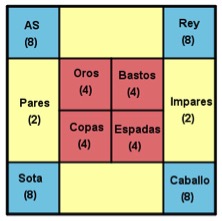
1. El azar y la probabilidad.Por mucho que nos empeñemos los profesores de la ESO en profundizar en el álgebra y las funciones, si hay una parte de las matemáticas con las que convivimos toda la sociedad es el azar. Aunque no seamos aficionados a los juegos de azar, todos nos encontramos en situaciones en las que nos preguntamos qué será más probable para actuar en consecuencia. La enseñanza de la probabilidad tiene la dificultad de ser una rama de las matemáticas que suele ser complicada de entender en su totalidad, pues muchas veces cosas que pensamos que son evidentes nos sorprenden, al estudiarlas con detenimiento, llevando la contraria a nuestra intuición. Por ello, es conveniente adentrarse en su enseñanza de una forma práctica, realizando muchas actividades englobadas en un entorno reconocible. La ventaja de un primer acercamiento a esa disciplina, es que podemos realizar una gran multitud de experimentos aleatorios con mucho material que podemos manipular de una forma entretenida. Así, podemos extraer cartas de una baraja, lanzar dados de diferentes caras, hacer rodar una ruleta, extraer bolas de distintos color de una bolsa o lanza una o varias monedas, y después de realizar el experimento de una forma empírica pasar a lo interesante, el estudio del fundamento matemático que existe detrás. Lo llamativo es que no se suelen encontrar normalmente en los libros de texto muchos juegos de azar que sean especialmente atractivos, y que permitan también, una vez jugados, investigar las propiedades y en definitiva trabajar el azar que es el objetivo último. Ya en la sesión de juegos hemos dedicado algunos artículos a los juegos de azar. Comenzamos con el que quizás sea el más conocido o difundido, la carrera de caballosi. Justo el último artículo aparecido en la sesión de SUMA, la dedicamos a los juegos de azarii y el primer artículo original que se publicó en la sección de Divulgamat fue dedicada a los juegos de azar no transitivosiii. En la mayoría de los juegos de azar, el material que se utiliza suele ser los dados, bien directamente con sus resultados o a través de tableros, lo que se suele complementar con monedas y con ruletas. Pero no suele ser habitual encontrar juegos de azar que no utilicen esos elementos en su desarrollo, por ello, vamos a dedicar hoy un artículo a unos juegos que se realizan con cartas, (aunque ya incluimos uno en el artículo de los no transitivos) en general con una baraja corriente. En la mayoría de estos juegos se pretende fortalecer la idea del cálculo elemental de probabilidad y la de manejar sucesos que sean equiprobables o saber discernir cuáles tienen más o menos probabilidad de ocurrir. 2. Mayor o menor.Este juego está pensado desde dos hasta cuatro jugadores, y su objetivo es ser consciente de los sucesos que son más o menos probables. Se juega con una baraja francesa y sólo se necesita un papel y lápiz para ir anotando los puntos. Se considera que el as equivale a su valor 1, es decir, sería la primera carta de la escalera hasta el 13. Uno de los jugadores baraja el mazo de cartas y lo coloca boca abajo sobre la mesa. Levanta una de las cartas y la coloca boca arriba. El siguiente jugador, normalmente el que está a la derecha del jugador anterior, hace una predicción, que la siguiente carta que levante será mayor o menor que la que se ha mostrado. A continuación, levanta una carta del mazo y la coloca boca arriba sobre la que se había mostrado en el paso anterior. Si se cumple su predicción se anota un punto, si no coincide no se anota nada y en ambos casos pasa el turno al jugador de su derecha. Suele ser un juego bastante rápido, por lo que se suelen realizar varias partidas seguidas. Se juega de forma que el último jugador que ha levantado la carta y ha acabado el mazo, es el que ahora baraja las cartas y comienza el procedimiento visto anteriormente. Una duda surge cuando el que levanta la carta muestra una con el mismo valor que la que se había mostrado antes. Lo habitual es considerar que esa tirada no vale y el mismo jugador levanta la siguiente carta del mazo. Hay otra versión que es perder el turno si sale la misma carta, aunque en este caso se varían un poco las normas. Un jugador puede predecir que la carta siguiente será mayor o menor que la anterior y si lo logra se anota dos puntos, teniendo en cuenta que si sale carta con el mismo valor pierde el turno. Pero también puede no arriesgarse y decir que su carta será menor o igual que la anterior y si acierta sólo se anota un punto. Lógicamente lo mismo si se plantea mayor o igual. El estudio de este juego es muy complicado pues en cada momento las probabilidades van cambiando según las cartas que vayan saliendo. Pero obliga a estar muy pendiente del juego para ir observando las cartas que han aparecido, lo que influye en nuestra predicción. No creo que éste sea un juego interesante para hacer un estudio completo, pero sí para estudiar las probabilidades de cada valor y estimar en qué casos es más interesante subir o bajar. 3. El compatible.La primera vez que encontré este juego fue en unas fichas que enviaba gratuitamente la editorial SM a los centros educativos con material didáctico. En concreto, el material de matemáticas estaba realizado por el Grupo Azarquiel y se componía de fichas agrupadas en cuatro temas, uno de los cuáles era el de Juegos Matemáticos. Más recientemente, Ana García Azcárate ha recuperado ese juego en su blogiv. Este juego tiene el objetivo de manejar sucesos que sean compatibles e incompatibles. Pueden jugar desde dos hasta cuatro jugadores y se necesita una baraja española de 40 cartas a la que se le apartan los seis y siete, quedando las cartas del as al cinco junto a las figuras. Cada jugador dispondrá también de dos fichas con distinto color por jugador. También se necesita un tablero como el de la imagen y papel y lápiz para apuntar las puntuaciones.
Imagen 1: Tablero de El compatible. La dinámica del juego es la siguiente. a) Cada jugador extrae una carta de la baraja y el que tenga la puntuación más alta coloca sus dos fichas en alguno de los recuadros del tablero, con la condición de que deben ser recuadros con distinta puntuación. Siguiendo el turno por su derecha, cada jugador apuesta a dos sucesos de los que queden libres, siempre con la exigencia de que deben tener distinta puntuación. b) Una vez colocadas todas las fichas se baraja el mazo de cartas y se colocan boca abajo sobre la mesa. c) El primer jugador levanta una carta y la coloca boca arriba sobre la mesa. Todos los jugadores que hayan apostado a algún suceso compatible deben decir en voz alta “COMPATIBLE”, y se anotan los puntos correspondientes al recuadro donde tuvieran sus fichas. Por ejemplo, si el jugador saca la sota de bastos, dado que la sota corresponde a un 10 de puntuación, se anotan puntos todos los que hayan apostado a bastos, a sotas o a pares. d) Se sigue el turno sacando cada jugador una nueva carta del mazo. e) Se acaba la partida cuando se haya dado una vuelta completa cinco veces y se suman todos los puntos obtenidos. Gana el que haya ganado más puntos. Tal como he descrito es la propuesta del Grupo Azarquiel, aunque hay aspectos que se pueden modificar sin problemas. Por ejemplo, pueden jugar también cinco jugadores, ya que quedan casillas donde apostar. El número de cartas que se saca de la baraja depende de la cantidad de jugadores. Por ejemplo, si sólo juegan dos pueden seguir extrayendo cartas, mientras no se termine el mazo, como propone Azarquiel. Otra posibilidad es que algún jugador pueda colocar alguna de sus fichas en donde haya ficha de otro jugador, pero no cuando sólo juegan dos. Lo que me parece más interesante del juego es la investigación posterior. Una vez jugado se les plantea a los jugadores a qué creen que se debe la puntuación que hay en cada suceso. No cuesta mucho llegar a estudiar las probabilidades de cada suceso y comprobar que la puntuación es la inversa a la probabilidad ya que, disponiendo de 32 cartas, como nos ha quedado, las probabilidades serían: P(par) = P(impar) = 16/32 = ½ P(oros) = P(copas) = P(bastos) = P(espadas) = 8/32 = ¼ P(as) = P(sota) = P(caballo) = P(rey) = 4/32 = 1/8 Una vez que hemos comenzado con las probabilidades, también es interesante que hallen cuál es la probabilidad de los sucesos que han elegido. Por ejemplo, si un jugador ha elegido as y pares, en total habrá 20 de las 32 cartas de la baraja que nos darán puntos. Si se elige copas y caballos sólo tendremos 11 cartas con las que obtener puntuación, aunque en una de ellas, el caballo de copas, anotaremos puntos por los dos conceptos. Aunque al principio pueda parecer que hay mucha diferencia de cartas, hay que tener en cuenta los puntos que se obtienen en cada caso, pues en el primero podríamos obtener como máximo 32 puntos por pares y 16 por as, es decir, 48, mientras que en el segundo caso podríamos obtener 32 por copas y 16 por caballos, luego volvemos a tener 48 puntos. El juego está pensado para que todos los jugadores tengan la misma probabilidad de anotar. Pero el investigar las posibilidades de cada uno, hace que los alumnos estudien con ansia las probabilidades para intentar elegir los sucesos que le permitan ganar a los contrarios. Otra investigación es completar los dos recuadros del tablero que no tienen asignados sucesos. Se puede proponer, después de los estudios anteriores, que busquen dos sucesos que se puedan colocar en esas casillas libres, y que estudien qué puntuación se podría asignar en ese caso. Una de las que suele salir es similar a la división en pares e impares, y así obtendríamos en una casilla as o figura, y en la otra ni as ni figura y les correspondería dos puntos a cada suceso. Un error muy corriente que cometen las personas que no tienen mucho conocimiento del azar, es pensar que en general, todos los resultados son igualmente probables. Influidos por el hecho de que al lanzar una moneda o un dado, que estén bien construidos, la probabilidad de los resultados es la misma, llevan a hacer extensible ese resultado a otras situaciones, por ejemplo, a pensar que la probabilidad de que salgan dos caras al lanzar dos monedas es la misma de que salga una cara y una cruz. Por eso son interesantes aquellos juegos en que se descubre que no todos los resultados de un experimento aleatorio tienen por qué tener las mismas posibilidades de salir. Sobre todo por el estudio posterior que se hace del juego. Ya vimos un juego en el que queda en evidencia este resultado cuando vimos la carrera de caballos de la que hablamos al principio y ahora vamos a ver un par de juegos en la misma línea. 4. Los cuatro ases.Este juego aparece en el libro de probabilidad de Ana García Azcárate. Está pensado para dos jugadores. Da igual el tipo de baraja que se tome. Se toman los cuatro ases de la baraja, se mezclan y se colocan boca abajo sin que ningún jugador los vea. El primer jugador escoge uno de los cuatro ases, por ejemplo el de oros o el de rombos, el siguiente jugador levanta uno de los cuatro ases y si coincide con el que el otro jugador había elegido, se anota dos puntos, en caso contrario el primer jugador se anota un punto. Se vuelve a barajar las cartas y se colocan, de forma oculta, de nuevo boca abajo y se repite el proceso. Lo normal es mantener la misma elección en toda la partida. Siempre es el segundo jugador el que levanta y se anotan los puntos de la misma forma. Después de diez manos gana el jugador que tenga más puntos. Se pueden jugar varias partidas cambiando los puestos de primer y segundo jugador. Después del terminar el juego se puede plantear si es un juego justo, es decir, si los dos jugadores tienen las mismas posibilidades de ganar. Fácilmente se ve que el primer jugador tiene triple posibilidad de anotarse un punto, frente a la única posibilidad de anotarse dos del segundo jugador. Aunque es un aspecto que no suele verse en secundaria, se puede introducir fácilmente la idea de esperanza matemática o valor medio esperado, pues en los experimentos con resultados discretos es fácil hallarla ya que basta multiplicar la probabilidad de un resultado por la cantidad de veces que puede salir. En nuestro caso, en tres de las cuatro ocasiones el primer jugador se anota un punto y en una de las cuatro se anota dos puntos el segundo jugador. Por ello, la esperanza del primer jugador sería:
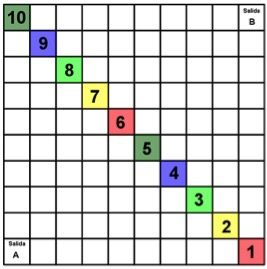
Como es algo que se entiende fácilmente en este ejemplo, nos puede servir de introducción al estudio de distintas juegos de los llamados socialmente de azar, para ver que, por ejemplo, en un casino siempre tiene mayor esperanza de ganar la empresa. 5. El juego de la cuadrícula.Este juego apareció en los libros de texto del Proyecto Azarquiel para Secundaria que editó, a finales del siglo pasado, Ediciones De La Torre. Concretamente en el texto para 2º de ESO. Posteriormente, Ana García Azcárate, componente original del grupo, lo recuperó hace unos años en su blogv. Aunque en su versión original la propuesta del juego era trabajar con dados, para que tuviese cabida en este artículo lo he adaptado a jugar con una baraja de cartas. En el blog de Ana se puede consultar la versión original. Tal como ella misma indica, éste es un juego de introducción a la probabilidad y a la Ley de los Grandes Números. Es un juego para dos jugadores y se necesita una ficha de distinto color para cada uno, una baraja de cartas española con 40 naipes, y un tablero como el de la imagen.
Imagen 2: Tablero para el Juego de la Cuadrícula. La forma de jugar es la siguiente: 1) Se baraja el mazo de cartas y cada jugador extrae una carta. Quien saque la puntuación mayor, escoge la casilla de salida colocando su ficha en dicha casilla. El contrario coloca la suya en la casilla opuesta. Se introducen las cartas extraídas en medio del mazo. 2) Cada jugador en su turno extrae una carta del mazo y mueve esa ficha según la carta extraída. Si la carta es un número (del 1 al 7) mueve la ficha una casilla en vertical y si es una figura en horizontal según el siguiente criterio:
3) Cuando la ficha de cada jugador llega a una casilla coloreada de la diagonal central (lo que ocurre después de extraer cada uno nueve cartas) el jugador se anota los puntos que aparezcan en esa casilla. 4) Acabada la partida, se colocan de nuevo las fichas en la casilla de partida y se vuelve a repetir la partida. Las cartas que se van utilizando se colocan en un montón de descartes. Después de dos partidas, se recogen todas las cartas, se barajan de nuevo y se juegan otras dos partidas más, manteniendo cada jugador la casilla inicial de salida. 5) Tras jugar las cuatro partidas (o más si lo estima el profesor) gana el jugador que haya anotado mayor puntuación. Una vez realizadas las partidas llega el momento de plantear al alumnado si el juego es equitativo, es decir, si los dos jugadores tienen las mismas posibilidades de ganar. Si los alumnos han estado atentos al juego y han visto el movimiento de las fichas, no cuesta mucho que lleguen a advertir que, tal como está diseñado el juego, las fichas se mueven mucho más rápidamente en vertical que en horizontal. La razón es obvia, de cada 10 cartas de un palo, en siete ocasiones se mueven en vertical y en tres en horizontal, por lo que la ficha que está en A se mueve más rápidamente hacia las casillas superiores, con mayor puntuación, mientras que la que sale de B se mueve hacia las casillas inferiores que tienen menor puntuación. Dado que estamos trabajando con el azar, puede ser que lo que esté previsto que pase (que gane el jugador A) no ocurra en realidad, pero como tendremos toda la clase jugando, lo anterior será algún caso aislado, por lo que utilizando la Ley de los Grandes Números, debe salir sin problemas que se cumple las previsiones anteriores. En la versión original del Grupo Azarquiel, además de usar dados el tablero es un poco más pequeño pues sólo llega hasta el 8. Otra variación es que el que primero llega a la diagonal se anota la puntuación y no el otro, pero esto sólo tiene sentido si en cada partida comienza uno distinto de los jugadores, ya que el primero que empieza es siempre el primero que llega a la diagonal. Otra variación es que el que elige casilla de salida coloca su ficha, pero quien empieza el juego es el segundo jugador, por lo que en cada partida hay que elegir la casilla de salida. En las reglas que yo he fijado, cada jugador saca una carta y se mueve según lo extraído. Después de varias partidas, se puede modificar esa regla y entonces el jugador que sea extrae una carta y los dos avanzan según la carta extraída, y se puede observar que el movimiento es simétrico respecto a la diagonal. 6. Referencia.GARCÍA AZCÁRATE, ANA (2013): Probabilidad y Geometría Espacial. Aviraneta, Madrid. Colección Pasatiempos y Juegos en clase de matemáticas.
Notas:[i] Se puede consultar en la sesión de juegos de divulgamat. http://www.divulgamat.net/index.php?option=com_content&view=article&id=10128&directory=67 [ii] http://www.divulgamat.net/index.php?option=com_content&view=article&id=16182&catid=77:juegos-matemcos&directory=67 [iii] http://www.divulgamat.net/index.php?option=com_content&view=article&id=17315&directory=67 [iv] https://anagarciaazcarate.wordpress.com/2015/11/20/probabilidad-el-compatible/ [v] https://anagarciaazcarate.wordpress.com/2017/05/16/el-juego-de-la-cuadricula-probabilidad/ |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |